הסתברות/משתנים מקריים/משתנים מקריים רציפים/התפלגות אקספוננציאלית

התפלגויות רציפות התפלגות יוניפורמית התפלגות אקספוננציאלית התפלגות נורמלית

מעריכי: $\ X\sim exp(\lambda )$

פונקצית התפלגות
פונקצית צפיפות
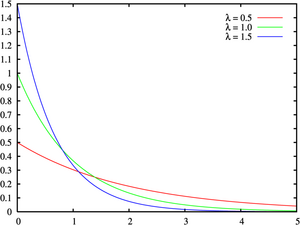
פרמטרים	$\ \lambda >0$
תומך	$\ x\in [0,\infty )$
פונקצית התפלגות	$\ 1-e^{-\lambda x}$
פונקצית צפיפות	$\ \lambda e^{-\lambda x}$
תוחלת	$\ 1 \over \lambda$
חציון	$\ \ln 2 \over \lambda$
שונות	$\ 1 \over \lambda ^{2}$
פונקציה יוצרת מומנטים	$\ \left(1-{\frac {s}{\lambda }}\right)^{-1}$
פונקציה אופיינית	$\ \left(1-{\frac {is}{\lambda }}\right)^{-1}$

אינטואיטיבית, התפלגות אקספוננציאלית (התפלגות מעריכית) היא ההתפלגות עד הזמן בו יקרה משהו, במקרה שבו הזמן עד שיקרה אותו הדבר אינו תלוי בזמן שכבר חיכינו.

הגדרה: התפלגות אקספוננציאלית (התפלגות מעריכית) נאמר כי מ"מ $X$ הוא בעל התפלגות אקספוננציאלית אם $f_{X}(x)=\left\{{\begin{array}{l l}\lambda e^{-\lambda x}&\quad x\geq 0\\0&x<0\\\end{array}}\right.,F_{X}(x)=\left\{{\begin{array}{l l}1-e^{-\lambda x}&\quad x\geq 0\\0&x<0\\\end{array}}\right.$ הקבוע $\lambda >0$ הוא קבוע הדעיכה. נכתוב $X\sim exp(\lambda )$.

נשים לב שככל ש-$\lambda$ גבוה יותר, הסיכוי שנחכה זמן רב קטן.

דוגמה

נניח ש-$X\sim exp(\lambda )$. מה הסיכוי שנקבל $X\geq \lambda$?

נשים לב כי

$\mathbb {P} (X\geq \lambda )=1-\mathbb {P} (X<\lambda )=1-F_{X}(\lambda )=e^{-\lambda ^{2}}$

.

חוסר זכרון

משתנה מקרי מעריכי הוא חסר זיכרון, כלומר לכל $s,t\geq 0$ מתקיים כי

$\,\!\mathbb {P} (X>s+t\;|\;X>s)=\mathbb {P} (X>t)$

המשמעות המילולית של תכונה זו היא כדלקמן: כשאנו ממתינים לאירוע שהזמן עד להתרחשותו מתפלג מעריכית, הזמן שחלף עד כה אינו משנה את התפלגות הזמן שנותר עד להתרחשות האירוע, וזמן זה (הזמן שנותר עד להתרחשות האירוע) ממשיך להתפלג מעריכית, בדיוק כאילו התחלנו להמתין זה עתה.

למעשה, מבין כל ההתפלגויות הרציפות, רק להתפלגות המעריכית תכונה זו.

ראשית נראה כי ההתפלגות המעריכית חסרת זכרון.

הוכחה: עפ"י הגדרת ההסתברות המותנית,

$\mathbb {P} (X>s+t\;|\;X>s)={\mathbb {P} (X>s+t\cap X>s) \over \mathbb {P} (X>s)}={\mathbb {P} (X>s+t) \over \mathbb {P} (X>s)}.$

לפי הגדרת ההתפלגות המעריכית נקבל, לכן,

$\mathbb {P} (X>s+t\;|\;X>s)={\mathbb {P} (X>s+t) \over \mathbb {P} (X>s)}={e^{-\lambda (s+t)} \over e^{-\lambda s}}=e^{-\lambda t}=\mathbb {P} (X>t)$

כעת נראה כי ההתפלגות המעריכית היא ההתפלגות הרציפה היחידה בעלת תכונת חוסר הזיכרון.

הוכחה: נניח התפלגות חסרת זכרון. היא צריכה לקיים את התכונה

$\,\!\mathbb {P} (X>s+t\;|\;X>s)={\mathbb {P} (X>s+t\;,\;X>s) \over \mathbb {P} (X>s)}={\mathbb {P} (X>s+t) \over \mathbb {P} (X>s)}=\mathbb {P} (X>t)$

מכאן נקבל את הדרישה:

$\mathbb {P} (X>s+t)=\mathbb {P} (X>s)\mathbb {P} (x>t).$

נתבונן, לכן, בפונקציה המקיימת

$f(s+t)=f(s)f(t).$

נציב $t=0$ ונקבל

$f(s+0)=f(s)=f(s)f(0),$

ומכאן נסיק

$f(0)=1$.

נקח שוב את השוויון המקורי, ונחסר מכל אגף $f(s)$:

$f(s+t)-f(s)=f(s)f(t)-f(s)=f(s)(f(t)-1)=f(s)(f(t)-f(0)).$

נחלק ב-$t$ ונשאיפו ל0:

$\lim _{t\rightarrow 0}{f(s+t)-f(s) \over t}=\lim _{y\rightarrow 0}f(s){f(t)-f(0) \over t}.$

מכאן קיבלנו את המשוואה הדיפרנציאלית:

$f'(s)=f(s)f'(0).$

תחת הנחות קלות למדי, פתרון משוואה זו הוא פונקציה מעריכית.

-

התפלגות אקספוננציאלית

-