הסתברות/התפלגויות וקטוריות

התפלגות ריילי

ריילי: $\ R\sim Rayleigh(r)$

פונקצית התפלגות
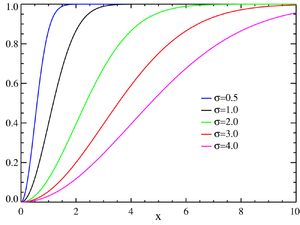
פונקצית צפיפות
פרמטרים	-
תומך	$\ r\in (0,\infty )$
פונקצית התפלגות	$\ 1-e^{-{r^{2} \over 2}}$
פונקצית צפיפות	$\ f_{R}(r)=re^{-{r^{2} \over 2}}$
תוחלת	$\ {\sqrt {\pi \over 2}}$
חציון	{{{חציון}}}
שונות	$\ 4-\pi \over 2$
פונקציה יוצרת מומנטים	?
פונקציה אופיינית	?

אם במשולש ישר זווית שני הניצב הם מ"מ גאוסים תקניים אז R הוא היתר.

יהיו $\ X,Y\sim N(0,1)$ מ"מ בלתי תלויים. נחשב את ההתפלגות של $\ R={\sqrt {X^{2}+Y^{2}}}$:

$\ \mathbb {P} (R\leq r)=\iint \limits _{X^{2}+Y^{2}\leq r^{2}}{1 \over {\sqrt {2\pi }}}e^{-{x^{2} \over 2}}{1 \over {\sqrt {2\pi }}}e^{-{y^{2} \over 2}}dxdy=$

$\ {1 \over 2\pi }\int \limits _{0}^{2\pi }\int _{0}^{r}e^{-{\rho ^{2} \over 2}}\rho d\rho d\theta =1-e^{-{r^{2} \over 2}}$

את פונקציית הצפיפות ניתן לקבל על ידי גזירה.

דוגמה

(להשלים)

סכום מ"מ כקונבולוציה

נניח כי נתונים שני מ"מ X₁, X₂ בלתי תלויים ואנו מעוניינים למצוא את פונקצית הצפיפות של הסכום. נחשב את פונקצית ההתפלגות שלהם (אינטגרל על $\ A={x_{1}+x_{2}\leq x}$):

$\ F_{X}(x)=\mathbb {P} (X_{1}+X_{2}\leq x)=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{x-x_{1}}f_{X_{1}}(x_{1})f_{X_{2}}(x_{2})dx_{2}dx_{1}$

על מנת לקבל את פונקצית הצפיפות נגזור את הביטוי שהתקבל:

$\ f_{X}(x)=\int \limits _{-\infty }^{\infty }f_{X_{1}}(x_{1})f_{X_{2}}(x-x_{1})dx_{1}$

קיבלנו, אם כן, כי הצפיפות היא קונבולוציה של הצפיפויות. לסיכום:

משפט: סכום מ"מ כקונבולוציה עבור שני מ"מ רציפים $\ X=X_{1}+X_{2}$ בלתי תלויים מתקיים: $\ f_{X_{1}+X_{2}}=f_{X_{1}}*f_{X_{2}}$ ובמקרה הבדיד: $\ p_{X_{1}+X_{2}}(n)=\sum \limits _{i=-\infty }^{\infty }p_{X_{1}}(i)p_{X_{2}}(n-i)$.

דוגמה: מ"מ בדיד

נחשב סכום עבור המשתנים $\ X_{1}\sim Pois(\lambda _{1})\ ,\ X_{2}\sim Pois(\lambda _{2})$:

$\ \mathbb {P} (X_{1}+X_{2}=n)=\sum \limits _{i=0}^{n}\mathbb {P} (X_{1}=i)\mathbb {P} (X_{2}=n-i)=\sum \limits _{i=o}^{n}e^{-\lambda _{1}}{\lambda _{1}^{i} \over i!}e^{-\lambda _{2}}{\lambda _{2}^{n-i} \over (n-i)!}=$

$\ =e^{-\lambda _{1}-\lambda _{2}}\sum \limits _{i=0}^{n}{n! \over i!(n-i)!}{\lambda _{1}^{i}\lambda _{2}^{n-i} \over n!}=e^{-\lambda _{1}-\lambda _{2}}\sum \limits _{i=0}^{n}{n \choose i}{\lambda _{1}^{i}\lambda _{2}^{n-i} \over n!}=e^{-\lambda _{1}-\lambda _{2}}{(\lambda _{1}+\lambda _{2})^{n} \over n!}\sim Pois(\lambda _{1}+\lambda _{2})$

לסיכום:

למה "סכום מ"מ פואסוניים" $\ Pois(\lambda _{1})*Pois(\lambda _{2})=Pois(\lambda _{1}+\lambda _{2})$

בדומה,

למה "סכום מ"מ בינומיים" $\ Bin(n_{1},p)*Bin(n_{2},p)=Bin(n_{1}+n_{2},p)$

דוגמה: מ"מ רציף

נחשב סכום עבור המשתנים $\ X_{1}\sim Exp(\lambda _{1})\ ,\ X_{2}\sim Exp(\lambda _{2})$:

$\ \mathbb {P} (X_{1}+X_{2}=x)=f_{X_{1}+X_{2}}(x)=\int \limits _{0}^{x}\lambda _{1}e^{-\lambda _{1}x_{1}}\lambda _{2}e^{-\lambda _{2}(x-x_{1})}dx_{1}=\lambda _{1}\lambda _{2}\int \limits _{0}^{x}e^{x_{1}(\lambda _{2}-\lambda _{1})-\lambda _{2}x}dx_{1}=$

$\ ={\lambda _{1}\lambda _{2} \over \lambda _{2}-\lambda _{1}}(e^{-\lambda _{1}x}-e^{-\lambda _{2}x})$

כפי שניתן לראות, התוצאה היא מעין מיצוע של שתי הצפיפויות המקוריות.

אם לעומת זאת נגדיר: $\ X_{1},X_{2}\sim Exp(\lambda )$ אז נקבל:

$\ f_{X_{1}+X_{2}}(x)=\lambda ^{2}xe^{-\lambda x}\sim Gamma(2,\lambda )$

זהו פילוג גאמה עם r=2, אשר עליו נלמד בהמשך.

התפלגות גאמה

גאמה: $\ X\sim \Gamma (r,\lambda )$

פונקצית התפלגות
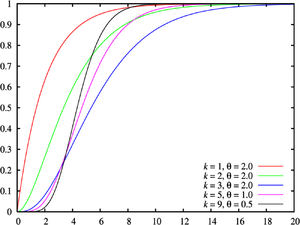
פונקצית צפיפות
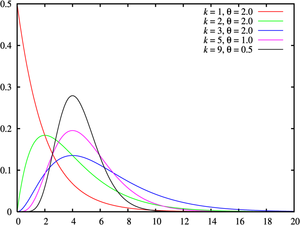
פרמטרים	$\ r,\lambda$
תומך	$\ x\in (0,\infty )$
פונקצית התפלגות	$\ 1-e^{-\lambda x}\sum \limits _{k=0}^{r-1}{(\lambda x)^{k} \over k!}$
פונקצית צפיפות	$\ f_{X}(x)={\lambda ^{r}x^{r-1}e^{-\lambda x} \over (r-1)!}$
תוחלת	$\ r \over \lambda$
חציון	{{{חציון}}}
שונות	$\ r \over \lambda ^{2}$
פונקציה יוצרת מומנטים	$(1-{s \over \lambda })^{-r}\ ,\ s<\lambda$
פונקציה אופיינית	$(1-{is \over \lambda })^{-r}$

סכום של r מ"מ מעריכיים אשר כל אחד מהם בעלי פרמטר λ,
כלומר: $\ X=X_{1}+...+X_{r}\ ,\ X_{i}\sim exp(\lambda )$.
.

תכונות

• $\ \Gamma (1,\lambda )=Exp(\lambda )$
• קונבולוציה: $\ \Gamma (r+s,\lambda )=\Gamma (r,\lambda )*\Gamma (s,\lambda )$.

התפלגות מולטינומית

דוגמה

-

התפלגויות וקטוריות

-