מבני נתונים ואלגוריתמים - מחברת קורס/שיעורי בית 3/תשובות
1
[עריכה]1
[עריכה]נוכיח את הסופיות והנכונות באינדוקציה על (אורך הקטע), אותו נגדיר כ.
הוכחה: (בסיס האינדוקציה) כאשר (הקטע ריק) או (קטע בעל איבר יחד), אז הפונקציה חוזרת ישר בלי לשנות את המערך (רואים זאת מ1-2). הפונקציה סופית ונכונה במקרים אלה, לכן.
(מעבר האינדוקציה) נניח סופיות ונכונות עד (לא כולל). נניח שמכניסים מערך בעל גודל . שורה 5 קוראת לPartition, אשר מחלקת את המערך לשני חלקים: Values[b, ..., p] וValues[p + 1, ..., e], כך ש, וכל איבר בחלק הראשון קטן או שווה לכל איבר בחלק השני (בשאלה נאמר שמותר להניח זאת, אך אפשר גם לוודא זאת מהתבוננות בPartition). שימו לב שהיות ש, אז אורך כל אחד משני החלקים קטן ממש מ. עפ"י הנחת האינדוקציה, 6-7 ימיינו כל אחד משני החלקים (ואף בזמן סופי). אם שני החלקים ממויינים, וכל איבר בחלק השמאלי קטן או שווה לכל אחד מאיברי החלק הימני, אז בהכרח כל המערך ממויין.
2
[עריכה]נתחיל במספר נקודות המשותפות לסעיף זה ולסעיף הבא. נגדיר את זמן הריצה על קלט בגודל כ.
הקריאה לפונקציה וביצוע השורות 1-4 עולות , וPartition ב5 עולה .
בסעיף זה, 6 פועלת על מערך בעל אורך , ו7 פועלת על מערך בעל אורך . שורות אלה, על כן, פועלות בזמן . נקבל, לכן, את נוסחת הנסיגה .
נפתור נוסחה זו בעזרת פרישה:
3
[עריכה]נשתמש בנקודות שצויינו בסעיף הקודם כמשותפות לשני הסעיפים.
בסעיף זה, 6 פועלת על מערך בעל אורך (בהזנחת שגיאות עיגול), ו7 פועלת ג"כ על מערך בעל אורך (שוב, בהזנחת שגיאות עיגול). שורות אלה, על כן, פועלות בזמן .
נקבל, לכן, את נוסחת הנסיגה . יש דרכים רבות לפתור נוסחת נסיגה זו - הפשוטה ביותר היא לזהות שזו נוסחת הנסיגה של מיון מיזוג, ולכן פתרונה .
2
[עריכה]הפתרון דומה מאד למיון ספירה. ראשית, הנה הפסוודו-קוד לInit:
# A global array.
1 Count
Init(Values, k)
1 Count = Make-Array(k)
2 for i in [1, ..., k]
3 Count[i] = 0
4 for j in [1, ..., Length(Values))
5 value = Values[j]
6 ++Count[value]
7 for i in [2, ..., k]
8 Count[i] = Count[i] + Count[i - 1]
המערך Count הוא משתנה גלובלי. הפונקציה Range מאתחלת אותו כך שהאיבר הi שלו מכיל את מספר האיברים הקטנים או שווים
לi בA. בניתוח מיון ספירה ראינו שהסיבוכיות היא .
לאחר שאתחלנו את המערך Count, הפונקציה Range פשוטה מאד. כל שעלינו לעשות הוא לחסר את מספר האיברים הקטנים מa ממספר האיברים הקטנים או שווים לb:
Range(a, b)
# First find the number of values less than a.
1 if a == 1
2 less-than-a = 0
3 else if a - 1 ≤ Length(Count)
4 less-than-a = Count[a - 1]
5 else
6 less-than-a = Count[Length(Count)]
# Now find the number of values less than or equal to b.
7 if b ≤ Length(Count)
8 at-most-b = Count[b]
9 else
10 at-most-b = Count[Length(Count)]
# The answer is obviously the difference between the two.
11 return at-most-b - less-than-a
קל לראות שהסיבוכיות היא .
3
[עריכה]א'
[עריכה]נתבונן בפסוודו-קוד עם memoization:
Min-Time(i, j)
1 if M[i][j] != Nil
2 return M[i][j]
3 if i == j
4 M[i][j] = 0
5 return 0
6 min-time = ∞
7 for k in [i, ..., j - 1]
8 guess = Min-Time(i, k) + Min-Time(k + 1, j) + PQR(i, k, j)
9 if guess M[i][j] < min-time
10 M[i][j] = min-time = guess
11 return min-time
נשים לב שאם נניח שכל קריאה רקורסיבית אורכת , אז יש לנו מספר קריאות שכ"א היא
(1-6, 11), ולולאה בת
איטרציות, כאשר כל איטרציה היא . זמן הריצה, לכן הוא
.
ב'
[עריכה]ההוכחה חוזרת, למעשה, על זו של דג הסלמון.
נצייר את עץ הקריאות הרקורסיביות, תוך לקיחה בחשבון את נושא הmemoization.

הציור אינו מראה את כל צמתי הקריאה מטעמי נוחות. הצומת קורא לצומת , בעקיפין לצמתים ו, ולעוד צמתים. הקווים המקווקווים מציינים שהקריאות אינן בהכרח ישירות.
חלק מהצמתים מודגשים, וחלק אינם:
- צומת מודגש אם הוא מתאר קריאה "רצינית", כלומר אחת שבה החלק העיקרי בפונקציה מתבצע (שורות 3-11 ב
Min-Time). - צומת אינו מודגש אם הוא מתאר קריאה "פושטית", בה לכל היותר רק חלק הmemoization מתבצע (שורות 1-2 ב
Min-Time).
נשים לב לנקודות הבאות:
- אם צומת לא מודגש, אז אין לו ילדים, ובנוסף, הוא (מדוע?)
- כל צומת מופיע מודגש פעם אחת (מדוע?)
ננתח כעת בשלבים, לפי הרעיון הבא. בכל שלב:
- ניקח צומת מודגש שאין לו ילדים מודגשים.
- ננתח את זמן הריצה שלו, ונרשום את התוצאה בצד. נשים לב שאם לצומת אין ילדים מודגשים, אז כל קריאה רקורסיבית שלו היא אכן (מפני שזו איננה ממש קריאה רקורסיבית). זמן הריצה שלו, לכן, הוא אכן .
- נמיר אותו בצומת לא מודגש, מפני שניתחנו כבר את חלק הקוד המסובך בו (ורשמנו אותו בצד). כל שנותר הוא הקריאה לפונקציה, והיא לוקחת .
נתחיל בצומת המודגש. לצומת זה אין כלל ילדים, ולכן זמן הקריאה הוא בבירור . נרשום בצד שעד כה הקריאות שעברנו עליהן עלו , ונחליף את הצומת בצומת לא מודגש. זה מסמן את העובדה שניתחנו כבר את החלק "עם הבשר" בצומת , וכל שנותר הוא .
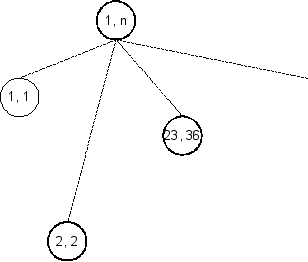
נחזור על אותה הפעולה עבור הצומת .

כנ"ל לגבי הצומת .
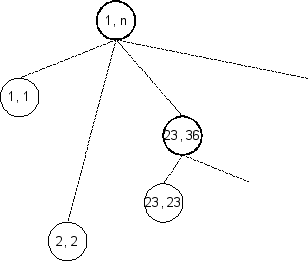
כעת נתבונן בצומת בשלב בו כל ילדיו אינם מודגשים. כל קריאה רקורסיבית של צומת זה כוללת שני מחירים:
- עצם הקריאה לפונקציה, שעולה
- זמן הקריאה האמיתי, שאותו כבר חייבנו (ורשמנו בצד), ולכן אין צורך לחייב אותו כאן שוב
הפועל היוצא הוא שבשלב זה, מותר לנו לחייב את הצומת אך ורק בקריאות רקורסיביות שעלות כל אחת מהן היא . זה בדיוק .
קל להשתכנע שבשלב בו נחליף את צומת הראש בצומת לא מודגש, רשמנו בצד את כל האיברים מהצורה
,
כאשר
ו. בצורה אחרת, מה שרשום בצד הוא
.
ג'
[עריכה]נשלב את שני הסעיפים הקודמים: .
כבר ראינו כיצד לפשט טור כפול זה בתרגילים בסדרי גדילה.
4
[עריכה]המבנה הרקורסיבי
[עריכה]נגדיר את כאיכות המשוקללת הגבוהה ביותר האפשרית כאשר יש עובדות ו פרוייקטים.
|
משפט: =
|
הוכחה: אם יש פרוייקט יחיד, אז ברור שכדאי להקצות את כל העובדות לו (שהרי נתון שהוספת עובדות אינה יכולה להוריד את איכות הפרוייקט). לכן, אם יש פרוייקט יחיד ו עובדות, נקבל שאיכותו הטובה ביותר היא .
נניח שיש
פרוייקטים. אם נקצה עובדות לפרוייקט ה, אז איכות הפרוייקט תהיה
,
ונוותר עם עובדות. על פי הגדרתנו, הוא הטוב ביותר שנוכל להשיג במקרה זה.
פסוודו-קוד
[עריכה]נתרגם את נוסחת הנסיגה הקודמת לפסוודו-קוד.
Max-Value(i, j)
1 if i == 1
2 return h(1) q(1, j)
3 max-value = 0
4 for j' in [0, ..., j]
5 guess = Max-Value(i - 1, j - j') + h(i) q(i, j')
6 if guess > max-value
7 max-value = guess
8 return max-value
הדפסת פרטי הפתרון
[עריכה]נוסיף עוד מטריצה גלובלית A כך שA[i][j] מתארת את מספר העובדות האופטימלי שכדאי להקצות לפרוייקט ה אם יש פרוייקטים ו עובדות.
להלן הקוד המכיל את השינויים הנדרשים:
Max-Value(i, j)
1 if i == 1
2 A[1][j] = j
3 return h(1) q(1, j)
4 max-value = 0
5 for j' in [0, ..., j]
6 guess = Max-Value(i - 1, j - j') + h(i) q(i, j')
7 if guess > max-value
8 A[i][j] = j'
9 max-value = guess
10 return max-value
כעת נשתמש במטריצה כדי להדפיס את האלוקציות האופטימליות:
Print-Assignments(i, j)
1 if i == 0
2 return
# The optimal assignment assigns j' workers to project i.
3 j' = A[i][j]
4 Print('Assign ' + j' + ' workers to project ' + i)
5 Print-Assignments(i - 1, j - j')
כך נפעיל את שתי הפונקציות:
1 A = Make-Matrix(k, n)
2 max-value = Max-Value(k, n)
3 Print(max-value)
4 Print-Assignments(k, n)
הוספת תזכור (memoization)
[עריכה]הפסוודו-קוד הרקורסיבי שמימש את הנוסחה הרקורסיבית, פותר אותן בעיות שוב ושוב. נייצר מטריצה גלובלית M שתשמור את התוצאות שקיבלנו, ונאתחל איברי מטריצה זו לNil. הפסוודו-קוד הבא מראה את השימוש במטריצה M. לשם הפשטות, השמטנו את חלקי הקוד המעדכנים את המטריצה המשמשת להדפסת ההשמות.
Max-Value(i, j)
1 if i == 1
2 M[1][j] = h(1) q(1, j)
3 return h(1) q(1, j)
4 max-value = 0
5 for j' in [0, ..., j]
6 guess = Max-Value(i - 1, j - j') + h(i) q(i, j')
7 if guess > max-value
8 M[i][j] = guess
9 max-value = guess
10 return max-value
ניתוח סיבוכיות
[עריכה]כרגיל, נגדיר את
כזמן הריצה של
Max-Value(i, j)
כאשר כל קריאה רקורסיבית היא . קל לראות שמתקיים
כרגיל, נמצא את זמן הריצה האמיתי של הקריאות הרקורסיביות כך:
יש לקחת בחשבון גם את זמן הריצה של אתחול המטריצה (M ואת הדפסת פרטי הפתרון:
- אתחול המטריצה אורך
- הדפסת הפרטים אורכת
הסיבוכיות הכוללת, לכן, היא
5
[עריכה]המבנה הרקורסיבי
[עריכה]נגדיר כ את העלות הזולה ביותר לטיפול בקטע באורך .
|
משפט: נתונה על ידי נוסחת הנסיגה הבאה:
|
הוכחה: נשים לב לנקודות הבאות:
- אם , אז אין מה לחתוך; ההובלה תעלה .
- אם , אז או שלא חותכים את הקטע, או שכן. אם לא חותכים, עלות השבירה 0, ועלות ההובלה . אם חותכים בנקודה , אז עלות הטיפול בחלק השמאלי תהיה , עפ"י ההגדרה, , עלות השבירה היא כמובן , ועלות הטיפול בחלק הימני תהיה, עפ"י ההגדרה, . נותר לקחת מינימום על פני , ולהחליט האם לחתוך או לא.
כדאי לדעת: אפשר כמובן לחשוב על מבנה רקורסיבי אחר לבעיה, כמו לדוגמה המבנה בדג הסלמון. |
מימוש נאיבי
[עריכה]להלן פסוודו-קוד המממש את נוסחת הנסיגה.
Min-Cost(i)
1 if i == 1
2 return F(1)
3 guess-without = F(i)
4 guess-with = ∞
5 for j in [1, …, i - 1]
6 if guess-with> Min-Cost(j) + k + Min-Cost(i - j)
7 guess-with = Min-Cost(j) + k + Min-Cost(i - j)
8 if guess-with < guess-without
9 return guess-with
10 else
11 return guess-without
שימוש בmemoization
[עריכה]נוסיף memoization.
Min-Cost(i)
1 if M[i] != Nil
2 return M[i]
1 if i == 1
2 M[1] = F(1)
3 return F(1)
4 guess-without = F(i)
5 guess-with = ∞
6 for j in [1, … i - 1]]
7 if guess-with> Min-Cost(j) + k + Min-Cost(i - j)
8 guess-with = Min-Cost(j) + k + Min-Cost(i - j)
9 if guess-with M[i] < guess-without
10 M[i] = guess-with
11 return guess-with
12 else
13 M[i] = guess-without
14 return guess-without
(נניח שהמערך הגלובלי Mבאורך nמאותחל תחילה כולו לNil.)
הדפסת נקודות השבירה
[עריכה]נוסיף גם מספיק מידע לצורך הדפסת פרטי הפתרון.
Min-Cost(i)
1 if M[i] != Nil
2 return M[i]
1 if i == 1
2 M[1] = F(1)
3 Break[1] = Nil
4 return F(1)
5 guess-without = F(i)
6 guess-with = ∞
7 for j in [1, … i - 1]]
8 if guess-with> Min-Cost(j) + k + Min-Cost(i - j)
9 guess-with = Min-Cost(j) + k + Min-Cost(i - j)
10 if guess-with
11 Break[i] = j
12 if guess-with
13 M[i] = guess-with
14 return guess-with
15 else
16 M[i] = guess-without
17 return guess-without
המערך הגלובלי Break מכיל את ההחלטה שעשינו לגבי כל קטע. Break[i]הוא Nilאם החלטנו לא לחלק את הקטע, והוא אם החלטנו לשבור בנקודה j.
כעת נדפיס את העצירות, ע"י קריאה לPrint-Breaks(n, 0). הפונקציה מוגדרת להלן.
Print-Breaks(i, start)
1 if Break[i] == Nil
2 return
3 j = Break[i]
4 Print(j + start)
5 Print-Nums(j, start)
6 Print-Nums(i - j, start + j)
הפונקציה מקבלת שני ארגומנטים: אורך הקטע, i, ותחילת הקטע, start. נניח שהפונקציה נקראה עבור שני ערכים ספיציפיים כאלה. אם Break[i] == Nil, אז לא חתכנו את הקטע, ואין מה להדפיס. אם לא, וBreak[i] == j, אז יש להדפיס את הנקודה j(תוך זכירה שאנו נמצאים startמתחילת כל הגשר), את החלק השמאלי, ואת החלק הימני.
ניתוח סיבוכיות
[עריכה]נגדיר את זמן הריצה של Min-Time(i) בהנחה שכל קריאה רקורסיבית היא כ. קל לראות ש. זמן הריצה חסום מלמעלה על ידי
.
גם כאשר לוקחים בחשבון את האתחול והדפסת הפרטים, הפתרון עדיין .
6
[עריכה]פסוודו-קוד
[עריכה]להלן הפסוודו-קוד לאלגוריתם:
ּSelection-Sort(Values)
1 for i in [1, ..., n - 1]
2 min = i
3 for j in [i + 1, ..., n]
4 if Values[j] < A[min]
5 min = j
# Exchange Values[i] and Values[min]
6 Values[i] <-> Values[min]
הוכחת נכונות
[עריכה]הנכונות מתבססת על המשפט הבא:
|
משפט: בסוף האיטרציה ה של 1-6,
|
קל להוכיח את המשפט באינדוקציה דומה לזו של מיון הכנסה.
הוכחת נכונות
[עריכה]קל להראות שהסיבוכיות היא , ושיש קלט שעבורו הסיבוכיות היא , וגם זאת בצורה דומה למה שראינו בזו של מיון הכנסה.
7
[עריכה]נטפל בבעיה זו בתרגול התגבור בנושא.



















![{\displaystyle \displaystyle \sum _{i=1}^{n}[\Theta (i)+T(1)]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48a2363c82d890bd8924f304ad55c40f71a7088d)
![{\displaystyle \displaystyle \sum _{i=1}^{n}[\Theta (i)]+\sum _{i=1}^{n}[]T(1)]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84fce8240d40e4e9e2ad7588b346d0b3bac4a9ab)




















![{\displaystyle \displaystyle \sum _{i=1}^{n}\sum _{j=i}^{n}[T'(i,j)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ae38e778ef073cb14ec77a348cdb1640a45e465)
![{\displaystyle \displaystyle T(1,n)=\sum _{i=1}^{n}\sum _{j=i}^{n}[T'(i,j)]=\sum _{i=1}^{n}\sum _{j=i}^{n}[\Theta (j-i+1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604076f6f11f2661c863b47f3aa88692fdfc4f0a)





![{\displaystyle \displaystyle \max _{j'\;|0\leq j'\leq j}\left[h(i)q(i,j')+m(i-1,j-j')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39977a41d4cece29b9ccfda8b4c4fc0d32ea5057)







![{\displaystyle \displaystyle \sum _{i=1}^{k}\sum _{j=1}^{n}[T'(i,j)]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/464efe1d8d1f7d161202c0447eb22708d01dfa03)
![{\displaystyle \displaystyle \sum _{i=1}^{k}\sum _{j=1}^{n}[\Theta (j)]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93aa5e333b0a5acf0068dc6744dad4b326bd5fca)
![{\displaystyle \displaystyle \sum _{i=1}^{k}[\Theta (n^{2})]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae8a64ec8ce4c4a1984fdb3338657978cf9be77)













![{\displaystyle \displaystyle \sum _{i=1}^{n}[T'(i)]=\sum _{i=1}^{n}[\Theta (i)]=\Theta (n^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c78d21dd4782631b287c39b4a4c50ea86323e979)

