מבני נתונים ואלגוריתמים - מחברת קורס/מבני נתונים/תורי קדימויות
דף זה עוסק בתורי קדימויות, בפרט במימוש ערימה בינרית (binary heap). תור קדימויות משמש לשמירת קבוצת איברים כאשר:
- הקבוצה דינמית (נתן להוסיף ולמחוק איברים).
- יש לענות בצורה יעילה על השאלה מהו האיבר הקטן ביותר (או לחלופין הגדול ביותר).
לעומת זאת, תור קדימויות אינו משמש לשמירת קבוצת איברים כאשר יש לחפש בצורה יעילה איבר מסוים (כמו האם האיבר 124 מופיע בקבוצה).
כדאי לדעת: #בספר הקורס, הפרק "Heapsort" עוסק בנושאים אלה.
|
|
מימוש C++ |
ממשק
[עריכה]הנה הממשק של תור קדימויות:
# Creates a priority queue.
Make-Heap()
# Inserts a value (v) to a priority queue (pq).
Insert(pq, v)
# Returns the smallest value in a priority queue (pq).
Min(pq)
# Removes the smallest value from a priority queue (pq).
Delete-Min(pq)
# Returns the size of a priority queue (pq).
Size(pq)
ולהלן דוגמה לשימוש בו:
1 Insert(pq, 94)
2 Insert(pq, 91)
3 Insert(pq, 99)
4 Insert(pq, 93)
# Prints 91.
5 Print( Min(pq) )
# Removes 91.
6 Delete-Min(pq)
# Removes 93.
7 Delete-Min(pq)
# Prints 94.
8 Print( Min(pq) )
בדף זה נעסוק במימוש ספציפי לממשק זה - מימוש הערימה הבינרית (Binary-Heap). שאר הדף עוסק במימוש זה.

|
'שימו לב: הממשק והשימוש מתאימים לתור קדימויות המאפשר גישה לאיבר הקטן ביותר. באופן סמטרי, אפשר להגדיר תור קדימויות המאפשר גישה לאיבר הגדול ביותר. בתור זה, שתי הפעולותMax וDelete-Max.
|
ארגון המידע
[עריכה]שומרים מערך של האיברים, ומשתנה המציין כמה איברים נמצאים כרגע בשימוש:
Binary-Heap
# An array of the values stored.
1 Values
# The size (number of entries used in Values).
2 size
|
דוגמה: להלן דוגמה לערימה המכילה 9 איברים מתוך 12 איברים אפשריים:  |
ייצוג העץ
[עריכה]ילדים והורים
[עריכה]כאמור, המבנה הוא למעשה מערך, אלא שאפשר לחשוב עליו כעץ בינרי (עץ שבו לכל צומת יש לכל היותר שני ילדים):
- השורש הוא באינדקס 1.
- אם צומת הוא באינדקס , אז:
- ילדו השמאלי (אם יש לו) הוא באינדקס .
- ילדו הימני (אם יש לו) הוא באינדקס .
- אביו (אם יש לו) הוא באינדקס .
# Returns the index of the left child.
Left-Child(i)
1 return 2 * i
# Returns the index of the right child.
Right-Child(i)
1 return 2 * i + 1
# Returns the index of the parent.
Parent(i)
1 return ⌊i / 2⌋
|
דוגמה: להלן העץ המתאים למערך שראינו מקודם:  |
אחת התכונות המועילות של העץ המתקבל, הוא שגובהו לוגריתמי במספר האיברים:
|
משפט: אם הוא מספר האיברים ו הוא מספר הרמות בעץ, אז , ו. |
תכונת הערימה
[עריכה]|
הגדרה: עץ ערימה בינרית חייב לקיים את תכונת הערימה - כל מסלול מהשורש לעלה מייצר סדרת איברים מונוטונית לא-יורדת. |
|
דוגמה: בעץ שלעיל:
|
כדאי לדעת: יש המגדירים תכונה זו ככך שמדובר בעץ סדור חלקית. |

|
שימו לב: עץ ערימה בינרית אינו בהכרח מקיים את תכונת הBST. |
כדאי לדעת: עץ הערימה הבינרית הוא מבנה נתונים רקורסיבי: אם עץ הוא עץ ערימה בינרית תקין, אז גם ילדו השמאלי וילדו הימני של השורש הם שורשי עצים כאלה.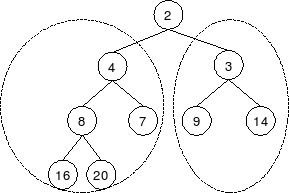 |
פעולות פשוטות
[עריכה]קל מאד לראות מתכונות הערימה את המשפט הבא.
|
משפט: האיבר הקטן ביותר בערימה נמצא באינדקס 1. |
בעזרת המשפט, נממש כעת את הפעולות הפשוטות Size, Max-Size, וMin. כ"א מהן היא באופן טריוויאלי.
# Returns the size of a heap (bh).
Size(bh)
1 return bh.size
# Returns the maximum size of a heap (bh).
Max-Size(bh)
1 return Length(bh.Values)
# Returns the smallest value in a heap (bh).
Min(bh)
1 return bh.Values[1]
פעולת Insert
[עריכה]כדי להכניס איבר חדש לערימה, ראשית מכניסים צומת חדש כצומת האחרון, ולאחר מכן מבעבעים אותו מעלה למקומו המתאים.
|
דוגמה: בתרשים הבא, A מראה ערימה בת 9 איברים; בB מוסיפים איבר חדש, מה שפוגם בתכונת הערימה; בC ובD מבעבעים את הצומת החדש כלפי מעלה.  |
להלן הפסוודו-קוד לפעולת Insert:
# Utility function for maintaining the heap invariant.
# Recursively corrects a violation at some index (i).
Bubble-Up(bh, i)
1 if i == 1
2 return
3 p = Parent(i)
4 if bh.Values[p] ≤ bh.Values[i]
5 return
# This swaps the two values.
6 bh.Values[p] <-> bh.Values[i]
7 Bubble-Up(bh, p)
# Inserts a value (v) to a binary heap (bh).
Insert(bh, v)
1 bh.Values[++bh.size] = v
2 Bubble-Up(bh, bh.size)
|
משפט: הפעולה |
הוכחה: ההוכחה היא באינדוקציה על גובה עץ הערימה, .
(בסיס האינדוקציה) עבור , קל לראות שאין צורך לתקן כלום וBubble-Up אכן אינה עושה כלום.
(מעבר האינדוקציה) נניח שהאלגוריתם מתקן עבור עצים שגובהם לכל היותר (כולל) , ונוכיח שהדבר נכון גם לעצים בגבה . נתבונן בעץ כלשהו בעל גבה שכרגע הכנסנו אליו איבר. קל לראות שגבה עץ ילדו השמאלי הוא בדיוק , וגבה עץ ילדו הימני הוא לכל היותר . כך או כך, מהנחת האינדוקציה, לאחר מספר קריאות רקורסיביות לBubble-Up, שני עצים אלה תקינים. התרשים הבא מראה את העץ במצב זה.

כעת יש מספר קטן של מקרים אפשריים:
- - במקרה זה, כל מסלול משורש לעלה הוא בהכרח מונוטוני. העץ, לכן, תקין, ו
Bubble-Upאכן לא תשנה כלום. - - במקרה זה בהכרח ההכנסה היתה לתת-העץ השמאלי (מדוע?), ולכן בהכרח . יוצא שהחלפה בין ו אכן תפתור את הבעיה, וקל לראות שזה מה ש
Bubble-Upתעשה בקריאה הרקורסיבית הבאה. - - מקרה זה סימטרי למקרה הקודם.
|
משפט:
|
|
משפט: אם לערימה יש איברים, אז |
פעולת Delete-Min
[עריכה]כדי להוציא את האיבר הקטן ביותר מהערימה, ראשית נחליף את צמתו בצומת האחרון, ולאחר מכן מבעבעים את הצומת מטה למקום המתאים.
|
דוגמה: בתרשים הבא, A מראה ערימה בת 9 איברים; בB מוציאים את האיבר הקטן ביותר (כלומר, מחליפים אותו בצומת האחרון), מה שפוגם בתכונת הערימה; בC ובD מבעבעים את הצומת כלפי מטה.  |
להלן הפסוודו-קוד לפעולת Delete-Min:
# Utility function for maintaining the heap invariant.
# Recursively corrects a violation at some index (i).
Bubble-Down(bh, i)
1 l = Left-Child(i)
2 r = Right-Child(i)
3 if l <= bh.size and bh.Values[l] and bh.size and bh.Values[l] < bh.Values[i]
4 smallest = l
5 else
6 smallest = i
7 if r <= bh.size and bh.Values[r] < bh.Values[smallest]
8 smallest = r
9 if smallest == i
10 return
# This swaps the two values.
11 bh.Values[i] <-> bh.Values[smallest]
12 Bubble-Down(bh, smallest)
# Removes the smallest value from a heap (bh).
Delete-Min(bh)
14 v = Min(bh)
15 bh.Values[1] = bh.Values[bh.size--]
16 Bubble-Down(bh, 1)
17 return v
|
משפט:
|
|
משפט: אם לערימה יש איברים, אז |
כדאי לדעת: בספר הקורס נקראת הפעולהBubble-Down בשם Heapify.
|
אלגוריתם המיון Heapsort
[עריכה]אפשר להשתמש בערימה בינרית כדי למיין מערך. להלן (גרסה אחת אפשרית) של אלגוריתם המיון Heapsort:
#/ Heap sort.
# Takes an array (Values), and sorts it in increasing order.
Heapsort(Values)
1 n = Length(Values)
2 bh = Make-Binary-Heap()
3 for i in [1, ..., Length(Values)]
4 Insert(bh, Values[i])
5 for i in [1, ..., Length(Values)]
6 Values[i] = Delete-Min(bh)
בשיעורי הבית תתבקש להוכיח את נכונות האלגוריתם ולהראות שסיבוכיותו .
בניה ממערך
[עריכה]לבסוף נעסוק בבעיה אחרונה - בניית ערימה בינרית ממערך (שגודלו ):
# Makes a binary heap from an array (Values).
Build-Heap(Values)
המימוש הנאיבי
[עריכה]לכאורה קל מאד לממש את {{קוד בשורה|Build-Heap ע"י לולאה של פעולות Insert:
# Makes a binary heap from an array (Values).
Build-Heap(Values)
1 bh = Make-Priority-Queue()
2 for i in [1, ..., Length(Values)]
3 Insert(bh, Values[i])
4 return bh
|
משפט: במימוש זה, |
מימוש בעזרת Bubble-Down
[עריכה]להלן מימוש יעיל יותר, המתבסס כולו על Bubble-Down:
# Makes a binary heap from an array (Values).
Build-Heap(Values)
1 bh = Make-Priority-Queue()
2 bh.size = Length(Values)
3 for i in [1, ..., Length(Values)]
4 bh.Values[i] = Values[i]
5 for i in [Length(Values), ..., 1]
6 Bubble-Down(bh, i)
7 return bh
|
משפט: מימוש זה אכן מייצר ערימה תקנית (כלומר כזו שמקיימת את תכונת הערימה). |
הוכחה: נתבונן ב5-6, ונחשוב על ייצוג העץ:

אפשר לראות שבכל פעם שBubble-Down נקראת, היא מופעלת על ערימה שיש בה הפרעה אחת לכל היותר - בראש הערימה. זהו בדיוק המצב שBubble-Down פותרת.
|
משפט: סיבוכיות המימוש היא . |
הוכחה: הטענה ברורה מ3-4.
את הטענה נוכיח כך. אם נמספר את הרמות כ, אז ברמה יש לכל היותר איברים. Bubble-Down המופעל על איבר ברמה אורך לכל היותר . לכן סיבוכיות 5-6 הנה במקרה הגרוע לכל היותר . נפשט ביטוי זה:
כבר ראינו לעיל ש, ולכן רק נותר להראות ש. אפשר להראות זאת בעזרת מעט אלגברה.
| הפרק הקודם: טבלאות ערבול |
תורי קדימויות תרגילים |
הפרק הבא: מבני נתונים לקבוצות זרות |





























![{\displaystyle \displaystyle \sum _{i=1}^{h}[2^{i-1}\Theta (h-i+1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b5151fee127e7ac053b272677175720d5c01ab5)
![{\displaystyle \displaystyle \sum _{i=1}^{h}[2^{i-1}\Theta (h-i+1)]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4623a2c650568edb946a1a0556d0808adfe81ede)
![{\displaystyle \displaystyle \sum _{i=1}^{h}[2^{h}2^{-(h-i+1)}\Theta (h-i+1)]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02ca8e9ae27b05e15e3f4cc15f73b252350abf74)
![{\displaystyle \displaystyle \sum _{j=1}^{h}[2^{h}2^{-j}\Theta (j)]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/426cbb132d1ca8ad5043e2c0b6bc6d0ec27338dd)
![{\displaystyle \displaystyle 2^{h}\sum _{j=1}^{h}[2^{-j}\Theta (j)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79e22f5099550a4ec81a91a7902702f9b7d49125)
![{\displaystyle \displaystyle \sum _{j=1}^{h}[2^{-j}\Theta (j)]=\Theta (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42c46e0816e705ee76f01f4d3e581b9f0e015d67)