מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/אלגוריתם Union-Find

מתוך ויקיספר, אוסף ספרי הלימוד והמדריכים החופשי.

< מבני נתונים ואלגוריתמים - מחברת קורס | גרפים

מבני נתונים ואלגוריתמים - מחברת קורס

הגדרה:

בהינתן גרף $\displaystyle G = (V, E)$ , רכיב הקשירות של $\displaystyle v \in V$ הוא קבוצת כל הצמתים שאפשר להגיע אליהם מ $\displaystyle v$ .

דף זו עוסק באלגוריתם לרכיבי קשירות בגרף לא מכוון.

כדאי לדעת:

בספר הקורס, הפרק "Disjoint Sets" (תת-פרק 1) מכסה נושא זה.

מימוש C++

boost::connected_components

[עריכה] הבעיה

נתון גרף לא מכוון $\displaystyle G = (V, E)$ . בהינתן שני צמתים כלשהם $\displaystyle u, v \in V$ , רוצים לדעת האם $\displaystyle v$ ברכיב הקשירות של $\displaystyle u$ (כלומר, האם יש מסלול ביניהם).

דוגמה:

באי באוקיינוס השקט יש שש ערים $\displaystyle 1-6$ . בעבר היו כל שתי ערים מחוברות זו לזו בדרך ישירה מאת לשניה. כעת, בעקבות שיטפון, אלה הדרכים היחידות שנותרו:

נרצה להיות מסוגלים, בהינתן $\displaystyle 2$ ו $\displaystyle 4$ לדוגמה, לענות האם הם עדיין נתן להגיע מהאחד לשני (במקרה זה - לא).

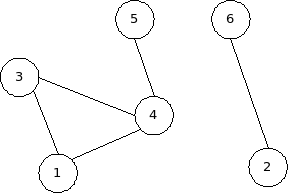
דוגמה:

במבני נתונים לקבוצות זרות, ראינו את הבעיה הבאה.

סטודנטים מתארגנים לקבוצות לימוד למבחן. נניח את ההנחה המקורבת שאם שני סטודנטים מחליטים ללמוד באותה קבוצה, אז הקבוצה שאליה שייך הסטודנט הראשון מתאחדת עם הקבוצה שאליה שייך הסטודנט השני. נרצה להיות מסוגלים, בהינתן שני סטודנטים, להחליט האם הם שייכים לאותה קבוצה או לא.נניח שיש שמונה סטודנטים: $\displaystyle 1-8$ . נתן לחשוב עליהם בתחילה כ-8 קבוצות זרות, שכ"א מורכבת מאיבר יחיד:

$\displaystyle 1$ ו $\displaystyle 2$ מחליטים ללמוד ביחד.
$\displaystyle 3$ ו $\displaystyle 4$ מחליטים ללמוד ביחד.
$\displaystyle 5$ ו $\displaystyle 6$ מחליטים ללמוד ביחד.
$\displaystyle 2$ ו $\displaystyle 5$ מחליטים ללמוד ביחד.
$\displaystyle 8$ ו $\displaystyle 2$ מחליטים ללמוד ביחד.

לבסוף, לכן, קבלנו את הקבוצות הזרות $\displaystyle \{1, 2, 5, 6, 8\}, \{3, 4\}, \{7\}$ :

נרצה להיות מסוגלים, בהינתן $\displaystyle 1$ ו $\displaystyle 7$ לדוגמה, לענות האם הם שייכים לאותה קבוצה (במקרה זה - לא).

כעת כשאנו מכירים גרפים מעט, נוכל לשים לב שאפשר להציג את הבעיה כאחת מתורת הגרפים. כל סטודנט מיוצג ע"י צומת, ואם שני סטודנטים מחליטים ללמוד ביחד, מייצגים זאת ע"י קשת ביניהם.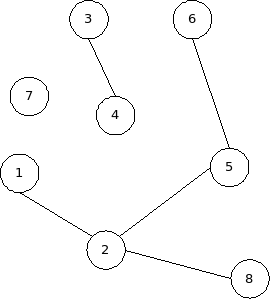

השאלה האם $\displaystyle 1$ ו $\displaystyle 7$ לדוגמה, שייכים לאותה קבוצה, שקולה לשאלה האם הם שייכים לאותו רכיב קשירות.

[עריכה] אלגוריתם Union-Find

להלן הפסוודו-קוד לאלגוריתם Union-Find, המשתמש במבנה הנתונים לקבוצות זרות שראינו:

Connected-Components(G)
1      V = V(G)
2      Sets = Make-Array( Length(V) )
 
3      for v in V
4              Sets[v] = Make-Set()
 
5      for (u, v) in E(G)
6              if Find-Set(Sets[u]) != Find-Set(Sets[v])
7                      Union(Sets[u], Sets[v])
 
8      return Sets

ולהלן דוגמה לשימוש בו:

1  Sets = Connected-Components(G)
 
        # Prints True.
1      Print( Find-Set(Sets[1]) == Find-Set([3]) )
 
        # Prints False.
2      Print( Find-Set(Sets[2]) == Find-Set([3]) )

הנה הסבר לUnion-Find:

ב2 מייצרים את המערך Sets, המכיל לכל צומת את הקבוצה שלו.
ב3-4 בונים לכל צומת קבוצה בגודל 1.
ב5-6 עוברים על כל הקשתות, ומאחדים, לכל קשת, את צומת ההתחלה וצומת הסוף של הקשת אם יש צורך.

[עריכה] ניתוח סיבוכיות

3-4 מייצרות $\displaystyle |V|$ קבוצות זרות שונות, ולאחר מכן מבצעים $\displaystyle \Theta(|E|)$ בדיקות, ולכל היותר $\displaystyle O(V)$ פעולות איחוד. לכן, מבחינת מבנה הנתונים לקבוצות זרות, מדובר בסדרה של $\displaystyle O(|E|) + O(|V|)$ פעולות, מתוכן $\displaystyle O(|V|)$ פעולות מסוג Make-Set. כפי שראינו בניתוח המימוש היעיל למבני נתונים לקבוצות זרות, הסיבוכיות היא $\displaystyle O(|V| \cdot \log(|V|) + |E| + |V|) = O(|V| \cdot \log(|V|) + |E|)$ , לכן.

כעת נותר לחשב את עלויות הלולאות עצמן. אם הגרף נתון ברשימת שכנויות, אז 3 אורכת $\displaystyle \Theta(|V|)$ , ו5 אורכת $\displaystyle \Theta(|E|)$ .

הסיבוכיות הכוללת, לכן, היא $\displaystyle O(|V| \cdot \log(|V|) + |E|)$ .

[עריכה] הקשר לאלגוריתם Grow-Tree

אפשר לחשוב עלהאלגוריתם שראינו זה עתה כמקרה פרטי של "אלגוריתם" Grow-Tree. כדי להדגיש זאת, הנה ווריאציה של האלגוריתם שמחזריה קבוצת קשתות עץ-פורש בהנתן גרף לא-מכוון קשיר.

Connected-Components(G)
1      V = V(G)
2      Sets = Make-Array( Length(V) )
 
3      E' = Make-List
 
4       for v in V
5               Sets[v] = Make-Set()
 
6       for (u, v) in E(G)
7               if Find-Set(Sets[u]) != Find-Set(Sets[v])
8                       Union(Sets[u], Sets[v])
9                       Insert(E', (u, v))
 
10     return E'

מהדימיון בין האלגוריתמים, קל לראות שכל מה שהוכחנו לגבי Grow-Tree תקף גם כאן: בהנתן גרף לא-מכוון וקשיר, ווריאציית האלגוריתם תבנה עץ פורש. בהרחבה פשוטה של ההוכחה, קל לראות שהאלגוריתם בונה יער במקרה הכללי של גרף לא-מכוון.

כדאי לדעת:

בקורס נלמד מספר אלגוריתמים (ודמויי-אלגוריתמים) לבניית עץ פורש. הם מתוארים בתרשים הבא:

"אלגוריתם" Grow-Tree בונה עץ פורש מגרף לא-מכוון קשיר. קל לשנותו כך שיבנה יער קטן ככל האפשר מגרף לא-מכוון.
אלגוריתם Union-Find מוצא את רכיבי הקשירות של גרף לא מכוון. קל לשנותו כך שיבנה עץ פורש מגרף לא מכוון קשיר.
"אלגוריתם" Grow-MST בונה עץ פורש מינימום מגרף לא-מכוון קשיר בעל טבלת עלויות לקשתות. הוא מקרה פרטי של Grow-Tree.
אלגוריתם Kruskal בונה עץ פורש מינימום מגרף לא-מכוון קשיר בעל טבלת עלויות לקשתות. הוא מימוש של Grow-MST.
אלגוריתם Prim בונה עץ פורש מינימום מגרף לא-מכוון קשיר בעל טבלת עלויות לקשתות. הוא מימוש של Grow-MST.

הפרק הקודם:
עצים

אלגוריתם Union-Find
תרגילים

הפרק הבא:
אלגוריתמים למציאת עפ"מ

מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/אלגוריתם Union-Find

מתוך ויקיספר, אוסף ספרי הלימוד והמדריכים החופשי.

תוכן עניינים

[עריכה] הבעיה

[עריכה] אלגוריתם Union-Find

[עריכה] ניתוח סיבוכיות

[עריכה] הקשר לאלגוריתם Grow-Tree

צפיות

כלים אישיים

ניווט

קהילה

חיפוש

תיבת כלים