מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/אלגוריתם Prim

מתוך ויקיספר, אוסף ספרי הלימוד והמדריכים החופשי.

< מבני נתונים ואלגוריתמים - מחברת קורס | גרפים

קפיצה אל: ניווט, חיפוש

מבני נתונים ואלגוריתמים - מחברת קורס

דף זו עוסק באלגוריתם למציאת העץ הפורש הזול ביותר בגרף לא מכוון בעל טבלת עלויות לקשתות.

כדאי לדעת:

אפשר לחשוב על אלגוריתם Prim כאלגוריתם Dijkstra בשינויים קלים.
בספר הקורס, הפרק "Minimum Spanning Tree" מכסה נושא זה.

מימוש C++

boost::prim_minimum_spanning_tree

[עריכה] הרעיון הכללי

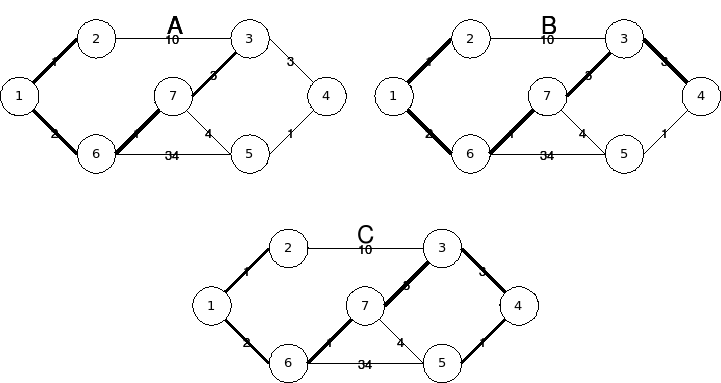
מתחילים מצומת שרירותי כלשהו, ובונים ממנו עץ גדל והולך. בכל שלב מוסיפים לו צומת חדש (שאינו שייך לעץ שלו), שהוא הזול ביותר להוספה.

דוגמה:

בתרשים הבא, A מתאר את הגרף בהתחלה. נבחר צומת כלשהו להתחיל בו, נניח צומת $\displaystyle 1$ . השלבים הראשונים הם כאלה:

העץ מכיל את $\displaystyle \{1\}$ . השכנים של צמתי העץ הם $\displaystyle 2$ ו $\displaystyle 6$ . הזול ביותר להוספה מביניהם הוא 2, ולכן נוסיף אותו.
העץ מכיל את $\displaystyle \{1, 2\}$ . השכנים של צמתי העץ הם $\displaystyle 6$ ו $\displaystyle 3$ . הזול ביותר להוספה מביניהם הוא 6, ולכן נוסיף אותו.
העץ מכיל את $\displaystyle \{1, 2, 6\}$ . השכנים של צמתי העץ הם $\displaystyle 3$ ו $\displaystyle 7$ . הזול ביותר להוספה מביניהם הוא 7, ולכן נוסיף אותו.

התרשים הבא ממשיך מהנקודה בה הפסקנו: יש כעת עץ בעל ארבעה צמתים, , ועוד שלשה עצים בעלי צומת יחד. נמשיך הלאה, לכן, עד שנקבל עץ יחיד.

[עריכה] פסוודו-קוד

להלן הפסוודו-קוד של אלגוריתם Prim. (הפסוודו-קוד מחזיר רק את מחיר העץ הפורש המינימום (ולא את קשתותיו). (בשיעורי הבית תתבקש לכתוב גרסה מלאה יותר.)

# Takes a connected undirected graph (G) and a cost table (W)
# Returns the cost of a set of edges E' such that (V(G), E') is 
#	a MST (minimum spanning tree).
MST-Prim(G, Edge-Costs)
1	pq = Make-Priority-Queue()
 
2	Min-Costs = Make-Array(Length(V(G)))
3	Used = Make-Array(Length(V(G)))
 
4	s = V[1]
 
5	for u in V(G)
6		Min-Costs[u] = u == s? 0 : ∞
7		Used[u] = False
8		Insert(pq, u)
 
9	total-cost = 0	
 
10	while Size(pq) &gt; 0
11		u = Delete(pq)
12		Used[u] = True
 
13		total-cost = total-cost + Min-Costs[u]
 
14		for v in A(G, u)
15			if Min-Costs[v] &gt; Edge-Costs[ (u, v) ] and Used[v] == False
16				Min-Costs[v] = Edge-Costs[ (u, v) ]
17				Decrease-Key(pq, v)
 
18	return total-cost

האתחול דומה מאד לזה שבאלגוריתם Dijkstra.‏ 1-8 דוחפות את כל הצמתים לתור קדימויות pq, ומאתחלות את Min-Costs כך שצומת המוצא הוא s. ההבדלים הם במערך Used,‏ ובמשמעות Min-Costs;‏ Used[u] מתאר האם כבר חיברנו את u לעץ של צומת המוצא s, וMin-Costs[u] מתאר את המחיר הזול ביותר (הידוע) שיעלה לחבר את u לעץ של צומת המוצא s.

כעת בלולאה 10-17 מוצאים כל פעם את הצומת u כך שu אינו בעץ של צומת המוצא s, אך עלות הוספתו היא הנמוכה ביותר. מעדכנים את העלות הכוללת ב13, ומחזירים עלות כוללת זו ב18 עם היציאה מהלולאה.

[עריכה] נכונות וסיבוכיות

בשיעורי הבית תתבקש להראות שהאלגוריתם למעשה מממש את "אלגוריתם" Grow-MST, ומכאן נובעת ההוכחה לנכונותו.

הסיבוכיות היא כסיבוכיות אלגוריתם Dijkstra ‏-‏ $\displaystyle \Theta((|V| + |E|) \cdot \log(|V|))$ , וזאת ע"י השוואה פשוטה של שני קטעי הפסוודו-קוד (אין כמעט הבדל ביניהם).

הפרק הקודם:
אלגוריתם Kruskal

אלגוריתם Prim

הפרק הבא:
חיפוש רוחבי

מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/אלגוריתם Prim

מתוך ויקיספר, אוסף ספרי הלימוד והמדריכים החופשי.

[עריכה] הרעיון הכללי

[עריכה] פסוודו-קוד

[עריכה] נכונות וסיבוכיות

צפיות

כלים אישיים

ניווט

קהילה

חיפוש

תיבת כלים

הדפסה/ייצוא