מבני נתונים ואלגוריתמים - מחברת קורס/אלגוריתמים/חיפוש לינארי ובינרי

לרוב מתחילים קורס אלגוריתמים בהגדרות מופשטות למדי לגבי מהו אלגוריתם. במקום זאת, נתחיל באלגוריתמים פשוטים מאד למציאת איבר במערך, ונלמד תוך כדי את ההגדרה לאלגוריתם, וכיצד מנתחים אלגוריתמים. בהרצאה זו נכסה את צורת העבודה בשליש הראשון של החומר (אלגוריתמים) באופן כללי. חלק גדול מפרטי הרצאה זו יובהרו לחלוטין רק בהרצאות הבאות. מומלץ לוודא שהרעיונות הכלליים מובנים בשלב זה, ובמהלך ההרצאות הבאות לחזור לכאן ולבדוק שהפרטים מתבהרים.

דף זה עוסק במציאת איבר במערך, לדוגמה, מציאת 7 במערך בתרשים הבא.

בעיית החיפוש.

נכסה שתי טכניקות: חיפוש לינארי וחיפוש בינרי.

כדאי לדעת: בספר הקורס, הפרק "Introduction" מכסה נושאים אלה.

חיפוש לינארי

הרעיון הבסיסי

חיפוש לינארי הוא פשוט מאד: עוברים על המערך משמאל לימין ב"קו" (ומכאן שמו, linear מלשון line), עד שמוצאים את האיבר המבוקש, או מגיעים לסוף המערך.

מימוש C++ std::find

פסאודו-קוד

יש מעט מאד רעיונות לפיתרון שפשוטים מספיק לתיאור מילולי (כמו "עוברים על המערך משמאל לימין"). כדי לתאר את רוב הפיתרונות, צריך לכתוב גם קוד בשפת תכנות כלשהי כדי שיהיה אפשר לעבור על פרטיו. כדי להתרגל לכך, להלן תיאור הקוד של חיפוש לינארי:

# Linear search.   
# Takes an array (Values) and a value (v).
# Returns an element if it matches the value (v), Nil otherwise.
Linear-Search(Values, v)
1	for i in [1, ..., Length(Values)]
2		if Values[i] == v
3			return Values[i]
		 		
4	return Nil

להלן הסבר לקוד. 1-3 עוברות בלולאה על איברי Values. אם 2 מוצאת איבר שהוא האיבר המבוקש v, מחזירים אותו (או מצביע אליו) ב3. אם לא נמצא האיבר המבוקש, מחזירים ערך ריק (או מצביע ריק) ב4.

מהי שפת התיכנות בה הקוד כתוב? זו אינה שפת תכנות אמיתית. היא מזכירה מעט גרסה מפושטת של שפת C (או, יותר מכך, פייתון). המטרה היא רק לכתוב את הרעיון כך שמי שיודע שפה כלשהי, יוכל לתרגם אותו בקלות לאותה שפה. בכל זאת, נשים לב למספר נקודות:

• אין צורך להגדיר טיפוסים של משתנים או פונקציות. אין צורך להגדיר האם משהו הוא משתנה או מצביע למשתנה. יש להבין את הדברים הללו מתוך ההקשר.
• אין צורך להשתמש בסוגריים מסולסלים כדי לתאר את הבלוק של פונקציה, תנאי, או לולאה. ההזחה משמשת לצורך כך.
• המערכים הנם מבוססי-1, כלומר האינדקס של איברם הראשון הוא 1 (שלא כבC, שם הוא 0).
• Nil הוא ערך מיוחד המסמן "כלום" (בדומה לNULL בשפת C).
• אם X הוא מערך, אז Length(X) מחזיר את ארכו.

כדאי לדעת: במהלך הקורס נראה מספר רב של אלגוריתמים שאפשר לכתוב להם ווריאציות טריוויאליות רבות. אין צורך לכתוב את האלגוריתם מחדש כל פעם. כאן, לדוגמה, לא נכתוב מחדש את האלגוריתמים עבור הדברים הבאים: ווריאציה שרק מחזירה True או False בהתאם לשאלה האם הערך נמצא במערך או לא. ווריאציה המקבלת מערך של מבנים (נניח Student, שלכל אחד מהם שדה id וgrade), ומחזירה מבנה שאחד משדותיו תואם ערך כלשהו (לדוגמה Student בעל id נתון).

הוכחת נכונות

לא כל רעיון שכתבנו אותו בפסאודו-קוד הוא אלגוריתם. צריך להראות שהרעיון אכן עובד, כלומר:

• יש להראות שהוא פועל בזמן סופי עבור קלט סופי (אם יש לולאות או קריאות רקורסיביות מסובכות, צריך להראות שהן אינן אינסופיות).
• יש להראות שהערך המוחזר נכון.

כאן בהקשר חיפוש לינארי, הוכחת הנכונות היא טריוויאלית. נוכיח בכל זאת את הנכונות כדי להתרגל לצורת ההוכחה.

הוכחה: נניח שv מופיע בValues באינדקס j. הלולאה 1 לאחר זמן מה תקבע את i לj.‏ 2 תמצא שאכן Values[j] שווה לv, ו3 אכן תחזיר את Values[j]. מצד שני, נניח שv אינו תואם שום דבר בValues. אז 2 לעולם לא תחליט שהאיבר נמצא. היות שהלולאה סופית (עבור קלט סופי), היא תסתיים לאחר זמן מה, ו4 תחזיר Nil.

ניתוח סיבוכיות

לאחר שכתבנו רעיון בפסאודו-קוד והוכחנו שהוא עובד, צריך לנתח את זמן הריצה שלו, כלומר כמה זמן ייקח לו לרוץ כפונקציה של גודל הקלט. כאן, לדוגמה, ננתח את זמן הריצה הגרוע ביותר בהנחה שהאיבר אכן נמצא במערך.

נקבע את $\displaystyle n$ כLength(Values).‏ כמה זמן אורכת שורה 2 במדויק? אי אפשר לדעת: זה תלוי במספר גורמים, כמו חומרת המחשב או שפת התכנות. לעומת זאת, נתן לדעת בוודאות שזמן זה הוא גודל חיובי (ממש) שאינו תלוי ב$\displaystyle n$.

הגדרה: כשגודל כלשהו הוא חיובי ממש, ואינו תלוי בגודל הקלט, נאמר שהוא $\displaystyle \Theta (1)$. נעסוק עוד בביטוי זה בסדרי גדילה.

לא כל הדברים הם $\displaystyle \Theta (1)$. לדוגמה, 2-3 אכן $\displaystyle \Theta (1)$, אבל 1-3 אינם $\displaystyle \Theta (1)$, מפני שאורך הלולאה תלוי בגודל הקלט $\displaystyle n$. בנקודה זו נוכל לומר, אבל, שאם v נמצא בValues אז Linear-Search אורכת $\displaystyle \Theta (1)+\Theta (1)\cdot n+\Theta (1)$ זמן במקרה הגרוע (שהוא כאשר האיבר שאותו מחפשים הוא האחרון בValues):

• הקריאה לפונקציה היא $\displaystyle \Theta (1)$.
• הלולאה 1-3 (ובפרט שורות 1-2) מתבצעת $\displaystyle n$ פעמים (במקרה הגרוע), וכל איטרציה אורכת $\displaystyle \Theta (1)$ זמן.
• השורה 3 מתבצעת פעם אחת והיא $\displaystyle \Theta (1)$.

כדאי לדעת: בסדרי גדילה -בסיס נלמד לפשט ביטוי זה, ונוכל להראות במדויק שסיבוכיות האלגוריתם הינה $\displaystyle \Theta (n)$ במקרה הגרוע.

נצייר גרף של $\displaystyle \Theta (1)+\Theta (1)\cdot n+\Theta (1)$:

זמן הריצה של חיפוש לינארי.

נשים לב שאיננו יודעים הרבה מעבר לצורת הגרף. ייתכן שהפונקציה דומה ל$\displaystyle 300+3\cdot n$, וייתכן שהפונקציה דומה ל$\displaystyle 3+300\cdot n$ (כל אחת מהן היא מהצורה $\displaystyle \Theta (1)+\Theta (1)\cdot n+\Theta (1)$). בכל אופן, מדובר בפונקציה לינארית.

עכשיו תורכם: נסה למצוא את זמן הריצה במקרים הבאים: המקרה הגרוע ביותר כאשר האיבר אינו במערך. המקרה הטוב ביותר כאשר האיבר במערך.

חיפוש בינרי

הרעיון הבסיסי

אם המערך ממויין, ביכולתנו לעשות משהו יעיל יותר. נתבונן בתחום הכולל של האיברים, ונשקול את היחס בין האיבר המבוקש לאיבר האמצעי בתחום. זה מחלק את התחום לשני תחומים - ימני ושמאלי. כעת:

• אם האיבר האמצעי הוא האיבר המבוקש - סיימנו.
• אם האיבר האמצעי גדול מהאיבר המבוקש, עלינו לחפש בתחום השמאלי. היות שהמערך ממויין, או שהאיבר המבוקש נמצא בתחום השמאלי, או שאיננו כלל במערך.
• באופן דומה, אם האיבר האמצעי קטן מהאיבר המבוקש, עלינו לחפש בתחום הימני.

התרשים הבא מראה את התחומים הראשונים בהם אנו מחפשים את 7:

מספר שלבים בחיפוש בינרי.

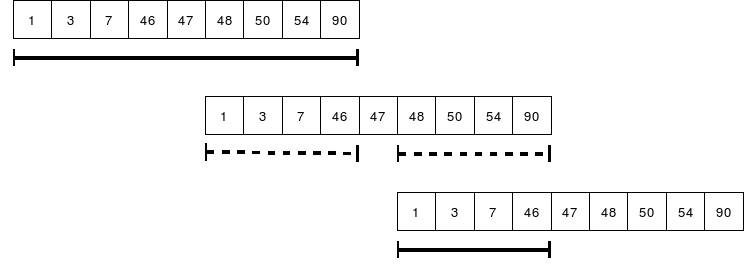
כדאי לדעת: חיפוש בינרי הוא אלגוריתם מסוג divide-and-conquer (הפרד ומשול): כדי לפתור בעיה "גדולה" (מציאת איבר במערך "גדול"), פותרים בעיה "קטנה יותר" (מציאת האיבר בתת-תחום).

מימוש C++ std::binary_search

עכשיו תורכם: נסה להסביר אינטואיטיבית מדוע זו צורת חיפוש יעילה הרבה יותר מזו של חיפוש לינארי.

פתרון

נניח שהמערך בעל 1,000,000 איברים. הבדיקה הראשונה של חיפוש לינארי תשלול איבר אחד (שאינו האיבר המבוקש), אך הבדיקה הראשונה של חיפוש בינרי תשלול בערך 500,000 איברים! במעט מחשבה אפשר להשתכנע שכל בדיקה של חיפוש בינרי תשלול לפחות אותו מספר איברים שתשלול בדיקה בחיפוש לינארי.

פסוודו-קוד

# Binary search. 
# Takes an array (Values) and a value (v).
# Returns an element if it matches the value (v), Nil otherwise.
# Note that the array (Values) must be sorted.
Binary-Search(Values, v)
1	return Binary-Search'(Values, v, 1, Length(Values))


# Binary search implementation. 
# Takes an array (Values), a value (v), and two boundaries (left and right).
# Returns an element if it matches the value (v), Nil otherwise.
# Note that the array (Values) must be sorted.
Binary-Search'(Values, v, left, right)
1	if left > right
2		return Nil
		
3	mid = ⌊(left + right) / 2⌋
		
4	if v < Values[mid]
5		return Binary-Search'(Values, v, left, mid - 1)

6	if v > Values[mid]
7		return Binary-Search'(Values, v, mid + 1, right)

8	return Values[mid]

הפונקציה Binary-Search אינה עושה דבר מלבד לקרוא לBinary-Search' ולהחזיר את הערך המוחזר ממנה. בפונקציה Binary-Search', המשתנים left וright הם "גבולות הגזרה" של תחום החיפוש. (Binary-Search תחילה קובעת אותם לאינדקס הראשון והאחרון של כל המערך, בקריאה הראשונה). 3 מחשבת את האינדקס האמצעי, 4-5 ו6-7 בודקות האם לחפש בתת-תחום שמאלי או ימני, ו8 מטפלת במקרה בו נמצא האיבר.

הוכחת נכונות

כאמור, הפונקציה Binary-Search אינה עושה דבר מלבד לקרוא לBinary-Search' ולהחזיר את הערך המוחזר ממנה. לכן רק נוכיח שהפונקציה Binary-Search' פועלת בזמן סופי (על קלט בגודל סופי), ומחזירה את התשובה הנכונה.

ראשית נוכיח סופיות.

הוכחה: הריקורסיה ממשיכה רק כל עוד left אינו גדול מright. כעת אם 4 הצליחה, אז בקריאה הבאה right קטנה ב1 לפחות; אם 6 הצליחה, אז בקריאה הבאה left גדלה ב1 לפחות; אחרת, 8 תתבצע, ולא תהיה כלל קריאה רקורסיבית נוספת.

כעת נוכיח שהערך המוחזר נכון.

הוכחה: נוכיח באינדוקציה שאמ"ם v נמצא בValues אז 8 מתבצעת. האינדוקציה היא על right - left + 1 (אורך התחום). נקרא לכך $\displaystyle n$.

(בסיס האינדוקציה) אם האורך $\displaystyle n$ הוא 0 או 1, אז מהתבוננות בקוד, הטענה נכונה.

(מעבר האינדוקציה) נניח שהטענה נכונה לכל $\displaystyle n'<n$. אם 4 מתקיימת, אז v קטן ממש מValues[mid]; הוא חייב להיות בתחום left עד mid - 1, או שאינו במערך כלל (שכן המערך ממויין). עפ"י הנחת האינדוקציה, נקבל את התשובה הנכונה. באופן דומה, אם 6 מתקיימת, אז נקבל את התשובה הנכונה. אם 8 מתבצעת, אז 4 ו6 לא התקיימו, ולכן Values[mid] חייב להיות שקול לv.

ניתוח סיבוכיות

שוב, נקבע את $\displaystyle n$ כLength(Values).

נגדיר את זמן הריצה של Binary-Search' על קלט בגודל $\displaystyle n$ כ$\displaystyle T(n)$.

עכשיו תורכם: לפי הגדרה זו, מהו זמן הריצה של Binary-Search על קלט בגודל $\displaystyle n$?

פתרון

$\displaystyle \Theta (1)+T(n)$

כ"א מ1, 2, ו3, 4, 6, ו8, אורכת $\displaystyle \Theta (1)$ זמן (הן אינן תלויות בגודל הקלט $\displaystyle n$). לכן, אם 8 אינה מתבצעת, אז האיטרציה הבאה תפעל על תחום שגודלו$\displaystyle \lfloor (n-1)/2\rfloor$. מכאן נקבל $\displaystyle T(n)=T(\lfloor (n-1)/2\rfloor )+\Theta (1)$.

כדאי לדעת: בסדרי גדילה נלמד לפשט ביטוי זה, ובנוסחאות נסיגה נלמד להראות במדויק שסיבוכיות האלגוריתם הנה $\displaystyle \Theta (\log(n))$ במקרה הגרוע.

בהמשך נראה שהפונקציה היא לוגריתמית, פחות או יותר. כלומר, פחות או יותר, $\displaystyle T(n)=\Theta (1)\cdot \left(\log(n+1)+\Theta (1)\right)$. מכאן נקבל שזמן הריצה של Binary-Search, שהוא $\displaystyle \Theta (1)+T(n)$, הנו $\displaystyle \Theta (1)+T(n)=\Theta (1)+\Theta (1)\cdot \left(\log(n+1)+\Theta (1)\right)$. שוב, נצייר ביטוי זה:

זמן הריצה של חיפוש בינרי.

נשים לב שאיננו יודעים הרבה מעבר לצורת הגרף. ייתכן שהפונקציה דומה ל$\displaystyle 300+3\cdot \left(\log(n+1)+50\right)$, וייתכן שהפונקציה דומה ל$\displaystyle 3+300\cdot \left(\log(n+1)+50\right)$ (כל אחת מהן היא מהצורה $\displaystyle \Theta (1)+T(n)=\Theta (1)+\Theta (1)\cdot \left(\log(n+1)+\Theta (1)\right)$). בכל אופן, מדובר בפונקציה לוגריתמית.

השוואה בין שתי שיטות החיפוש

ראינו שתי שיטות חיפוש בדף זה, חיפוש לינארי וחיפוש בינרי. יש ביניהן מספר הבדלים. בין היתר:

1. הראשונה עובדת לכל מערך, והשניה עובדת למערך ממויין.
2. יש להם זמני ריצה שונים עבור המקרה הגרוע ביותר של מציאת איבר שאכן נמצא במערך.

נתמקד מעט בנקודה השניה. אנו יודעים שזמן הריצה של חיפוש לינארי במקרה הגרוע הוא $\displaystyle \Theta (1)+\Theta (1)\cdot n+\Theta (1)$, כלומר משהו כזה:

זמן הריצה של חיפוש לינארי.

אנו יודעים שזמן הריצה של חיפוש בינרי במקרה הגרוע הוא $\displaystyle \Theta (1)+\Theta (1)\cdot \left(\log(n+1)+\Theta (1)\right)$, כלומר משהו כזה:

זמן הריצה של חיפוש בינרי.

למרות שאנו יודעים מעט מאד על זמני הריצה של שתי הפונקציות (לדוגמה, איננו יודעים האם הראשונה היא $\displaystyle 300+3\cdot n$ או $\displaystyle 3+300\cdot n$), קל מאד לראות שעבור קלטים גדולים מספיק, המקרה הגרוע של חיפוש בינרי הוא הרבה יותר מהיר מהמקרה הגרוע של חיפוש לינארי. מספיק לזהות שהראשונה היא פונקציה לינארית, והשניה היא פונקציה לוגריתמית.

עכשיו תורכם: הוכח שעבור ערכי $\displaystyle n$ גדולים מספיק, $\displaystyle a+b\left(log(n+1)+c\right)<d+e\cdot n+f$ (כאשר כל המקדמים חיוביים).

פתרון

על פי משפט ל'הוספיטל, $\displaystyle \lim _{n\rightarrow \infty }{\frac {a+b\left(log(n+1)+c\right)}{d+e\cdot n+f}}=0$

סיכום

בדף זה הגדרנו בעיה, ראינו שני אלגוריתמים שפותרים אותה, והשווינו ביניהם. שני הרעיונות החשובים שראינו הם אלגוריתמים וסדרי גדילה:

1. אלגוריתם הוא סידרת פעולות מוגדרת היטב שפותרת בעיה בזמן סופי. כדי להראות שרעיון לפיתרון בעיה הוא אלגוריתם, צריך לתאר את הפיתרון (במילים ובציורים כדי להבינו, ובפסוודו-קוד כדי לתארו בצורה מדוייקת יותר), ולהוכיח שפעולתו סופית ונכונה.
2. כדי לבחור איזה אלגוריתם פועל טוב יותר (עבור קלטים גדולים מספיק), אפשר לנתח את סדר הגדילה של כל אלגוריתם, כלומר, לזהות שאלגוריתם גדל "כמו לוגריתם", או "כמו פונקציה לינארית".

הפרק הקודם: אלגוריתמים

חיפוש לינארי ובינרי תרגילים

הפרק הבא: סדרי גדילה