מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/חיפוש רוחבי

מבני נתונים ואלגוריתמים - מחברת קורס

דף זו עוסק באלגוריתם למציאת המסלול הקצר ביותר בגרף מכוון מצומת מוצא כלשהו.

כדאי לדעת:

בספר הקורס, הפרק "Elementary Graph Algorithms" (תת פרק 2) מכסה נושא זה, אולם אנו נשתמש בגרסה מעט פשוטה יותר מזו המופיעה בספר.

מימוש C++

boost::breadth_first_search

הבעיה[עריכה]

נתונים גרף מכוון $\displaystyle G=(V,E)$ וצומת מוצא $\displaystyle s\in V$ כלשהו. בהינתן צומת $\displaystyle v\in V$ כלשהו, רוצים לדעת מהו המסלול הקצר ביותר מ $\displaystyle s$ ל $\displaystyle v$ .

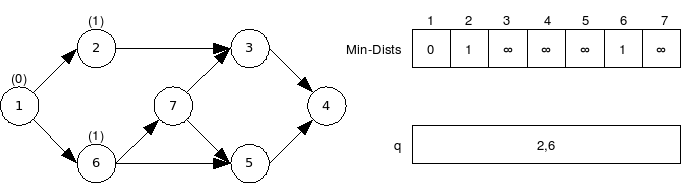
דוגמה:

בגרף הבא, נניח צומת מוצא $\displaystyle s=1$ .

רוצים למצא את המסלול הקצר ביותר מ $\displaystyle s$ לכל צומת אחר בגרף. המסלול הקצר ביותר ל $\displaystyle 3$ , לדוגמה, הוא $\displaystyle 1\rightarrow 2\rightarrow 3$ , וארכו 2.

חיפוש רחבי[עריכה]

הרעיון הכללי[עריכה]

במהלך מציאת הפתרון נחזיק שני מבני נתונים:

Min-Dists, מערך שיחזיק את המרחקים הקצרים ביותר.
q, תור שיחזיק את קבוצת הצמתים שאת מרחקיהם אנו קובעים כעת.

נפעל עפ"י הצעדים הבאים:

בתחילה נאתחל את כל איברי Min-Dists ל∞, למעט Min-Dists[s], שאותו נאתחל ל0; נכניס את s לq.
כל עוד q אינו ריק, נשלוף ממנו צומת, נעדכן את ערכי Min-Dists של שכניו, ונכניס אותם לתור עפ"י הצורך.

דוגמה:

עבור הגרף שראינו לעיל, וצומת המוצא $\displaystyle s=1$ , הנה המצב ההתחלתי:

כעת 1 בראש התור. נשלוף אותו ונעדכן את שכניו.

כעת 2 בראש התור. נשלוף אותו ונעדכן את שכניו.

כעת 6 בראש התור. נשלוף אותו ונעדכן את שכניו.

כעת 3 בראש התור. נשלוף אותו ונעדכן את שכניו.

כעת 7 בראש התור. נשלוף אותו ונעדכן את שכניו.

כעת 7 בראש התור, אבל אין את מי לעדכן - שכנו של 7 הוא 5, ול5 יש כבר מרחק ידוע של 3. לכן לא מכניסים את 5 לתור.

ממשיכים כך הלאה עד שהתור מתרוקן.

פסוודו-קוד[עריכה]

להלן הפסוודו-קוד לחיפוש רחבי:

BFS(G, s)
1	q = Make-Queue()

2	Min-Dists = Make-Array( Length(V(G)) )

3	for u in V(G)
4		Min-Dists[u] = u == s? 0 : ∞
	
5	Enqueue(q, s)
	
6	while Size(q) > 0
7		u = Dequeue(q)
	
8		for v in A(G, u)
9			if Min-Dists[v] > Min-Dists[u] + 1
10				Min-Dists[v] = Min-Dists[u] + 1
11				Enqueue(q, v)
                	
12	return Min-Dists

ולהלן דוגמה לשימוש בו:

1	Min-Dists = BFS(G, 1)

	# Prints 0.
2	Print( Min-Dists[1] )

	# Prints 2.
3	Print( Min-Dists[3] )
	
	# Prints 3.
4	Print( Min-Dists[4] )

הנה הסבר לBFS:

ב1 מייצרים את את התור q, וב2 מייצרים את את המערך Min-Dists.
הלולאה 6-11 פועלת כל עוד q אינו ריק.
7 מוציאה את האיבר הקדום ביותר שהוכנס ל בq, ו8-11 מעדכנת את שכניו.

נכונות[עריכה]

משפט:

ב11, Min-Dists מכיל את הערכים הנכונים.

שלבי התור[עריכה]

ראשית נוכיח את המשפט הבא, המתאר את מצב ההתור q במהלך הלולאה 6-11.

משפט:

התור q מכיל בכל עת סדרת צמתים מהצורה $\displaystyle u_{1},...,u_{i},v_{1},...,v_{j}$ , עבור $\displaystyle i,j\geq 0$ כלשהם, כך ש:

Min-Dists[u1] = ... = Min-Dists[ui] = $\displaystyle k$
Min-Dists[v1] = ... = Min-Dists[vj] = $\displaystyle k+1$

עבור $\displaystyle k$ כלשהו.

מה בעצם טוען המשפט?בלולאה 6-11, q מכיל תמיד 0 או יותר צמתים שרשום להם מרחק כלשהו, שלאחריהם 0 או יותר צמתים שרשום להם מרחק גדול ב1. לעולם לא נראה בו זמנית בq צמתים שלהם שלושה ערכים שונים בMin-Dists.

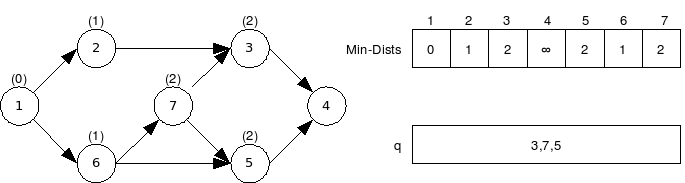
דוגמה:

בתחילת הדוגמה לעיל, הכיל q את הצומת 1, ואכן: Min-Dists[1] = $\displaystyle 0$ .
בדוגמה לעיל ראינו מצב שבו בq ישבו הצמתים 3, 7, 5, ואכן:
1. Min-Dists[3] = $\displaystyle 2$
2. Min-Dists[7] = Min-Dists[5] = $\displaystyle 3$

הגדרה:

נאמר שq מגיע לשלב $\displaystyle k$ בפעם הראשונה שבה בשורה 6, q מכיל צמתים שלכולם בדיוק אותו ערך $\displaystyle k$ בMin-Dists

דוגמה:

בפעם הראשונה שמגיעים לשורה 6, הכיל q את הצומת 1, והיות שMin-Dists[1] = $\displaystyle 0$ , אז q הגיע לשלב 0.

הוכחת הנכונות בעזרת שלבי התור[עריכה]

בעזרת אפיון תוכן התור בשלבים, נוכל להוכיח את המשפט הבא.

משפט:

כאשר q מגיע לשלב $\displaystyle k$ , אז q מכיל בדיוק את הצמתים שמרחקם הקצר ביותר מs הוא $\displaystyle k$ .

ראשית נשים לב שהמשפט למעשה אומר שני דברים:

כאשר q מגיע לשלב $\displaystyle k$ , אז מרחקו הקצר ביותר של כל צומת בq הוא $\displaystyle k$ .
אם מרחקו הקצר ביותר של צומת בq הוא $\displaystyle k$ , אז הצומת יהיה בq כאשר q מגיע לשלב $\displaystyle k$ .

להלן הוכחת המשפט.

הוכחה: ההוכחה היא באינדוקציה על $\displaystyle k$ .

(בסיס האינדוקציה) q נמצא בשלב 0 כאשר $\displaystyle s$ מוכנס אליו. קל לראות שהטענה מתקיימת: אכן מרחקו הקצר ביותר מ $\displaystyle s$ ל $\displaystyle s$ הוא 0, ואין צומת אחר שמרחקו מ $\displaystyle s$ הוא 0.

(מעבר האינדוקציה) נניח שהטענה נכונה עד לשלב ה $\displaystyle k-1$ (כולל), ונראה שהיא נכונה לשלב ה $\displaystyle k$ .

נתבונן בצומת $\displaystyle v$ שנמצא בתור בשלב $\displaystyle k$ . נניח שמרחקו הקצר ביותר מ $\displaystyle s$ גדול ממש מ $\displaystyle k$ . מתי הוכנס $\displaystyle v$ לתור? מתישהו בין שלב $\displaystyle k-1$ לשלב $\displaystyle k$ , כאשר מצאנו שהוא שכן של צומת $\displaystyle u$ משלב $\displaystyle k-1$ . אבל, לפי הנחת האינדוקציה, זה יש מסלול מ $\displaystyle s$ ל $\displaystyle u$ באורך $\displaystyle k-1$ , ולכן יש מסלול מ $\displaystyle s$ ל $\displaystyle v$ באורך $\displaystyle k$ . כלומר, אם $\displaystyle v$ בתור בשלב $\displaystyle k$ , אז מרחקו לכל היותר $\displaystyle k$ .

כעת ניקח צומת $\displaystyle v$ כלשהו (לא הצומת הקודם), שמרחקו מ $\displaystyle s$ הוא $\displaystyle k$ . אם זה המצב, אז קיים $\displaystyle u$ כלשהו כך שקיים מסלול מ $\displaystyle s$ ל $\displaystyle u$ כלשהו באורך $\displaystyle k-1$ , וכן יש קשת מ $\displaystyle u$ ל $\displaystyle v$ . (למעשה, ייתכן יותר מצומת יחיד כזה. נקרא בשם $\displaystyle u$ לצומת הראשון המקיים זאת.) לפי הנחת האינדוקציה, $\displaystyle u$ היה בתור בשורה 6 בשלב $\displaystyle k-1$ . אבל מ8-11, ברור שהצומת $\displaystyle v$ מוכנס לתור במהלך שלב זה.

ניתוח סיבוכיות[עריכה]

נניח שהגרף נתון ברשימת שכנויות.

1-2 פועלות בבירור בזמן $\displaystyle \Theta (|V|)$ .

3-5 מבצעות $\displaystyle |V|$ פעולות Enqueue, ולכן אורכות זמן $\displaystyle \Theta (|V|)$ במקרה הגרוע.

כפי שראינו, כל צומת נכנס לכל היותר פעם אחת לq, ולכן 6-11 רצה לכל היותר $\displaystyle |V|$ פעמים. 7 היא $\displaystyle O(1)$ , ולכן תורמת סה"כ‏ $\displaystyle O(|V|)$ .‏ 8-11 רצות $\displaystyle |N(u)|$ פעמים לכל צומת u, ולכן רצות סה"כ ‏ $\displaystyle |E|$ פעמים לכל היותר. 9-11 הן $\displaystyle O(1)$ , ולכן תורמות סה"כ ‏ $\displaystyle O(|E|)$ .