מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/אלגוריתם Dijkstra

מתוך ויקיספר, אוסף ספרי הלימוד והמדריכים החופשי.

< מבני נתונים ואלגוריתמים - מחברת קורס | גרפים

קפיצה אל: ניווט, חיפוש

מבני נתונים ואלגוריתמים - מחברת קורס

דף זו עוסק באלגוריתם למציאת המסלול הזול ביותר בגרף מכוון מצומת מוצא כלשהו.

כדאי לדעת:

בספר הקורס, הפרק "Single-Source Shortest Paths" (תתי פרקים 1 ו2) מכסה נושא זה.

מימוש C++

boost::dijkstra_shortest_paths

תוכן עניינים

1 הבעיה
2 אלגוריתם Dijkstra
- 2.1 הרעיון הכללי
- 2.2 פסוודו-קוד
3 נכונות
4 ניתוח סיבוכיות

[עריכה] הבעיה

נתונים גרף מכוון $\displaystyle G = (V, E)$ , טבלת עלויות לקשתות $\displaystyle E$ , וצומת מוצא $\displaystyle s \in V$ כלשהו. בהינתן צומת $\displaystyle v \in V$ כלשהו, רוצים לדעת מהו המסלול הזול ביותר מ $\displaystyle s$ ל $\displaystyle v$ .

שימו לב:

בדף זה לא נעסוק במחירי קשתות שאינם חיוביים.

דוגמה:

בגרף בתרשים הבא, המספר המצויין על כל קשת הוא עלות הקשת. נניח צומת מוצא $\displaystyle s = 1$ .

רוצים למצא את המסלול הזול ביותר מ $\displaystyle s$ לכל צומת אחר בגרף. המסלול הזול ביותר ל $\displaystyle 3$ , לדוגמה, הוא $\displaystyle 1 \rightarrow 6 \rightarrow 7 \rightarrow 3$ , ועלותו 6.

[עריכה] אלגוריתם Dijkstra

[עריכה] הרעיון הכללי

במהלך מציאת הפתרון נחזיק שני מבני נתונים:

Min-Costs, מערך שיחזיק את המרחקים הזולים ביותר.
pq (שיפורט בהמשך), שיחזיק את קבוצת הצמתים שעדיין אנו שוקלים את מסלולם הזול ביותר.

נפעל עפ"י הצעדים הבאים:

בתחילה נאתחל את כל איברי Min-Costs ל∞, למעט Min-Costs[s], שאותו נאחל ל0; נכניס את כל הצמתים לpq.
כל עוד pq אינו ריק, נשלוף ממנו את הצומת u שעבורו Min-Costs[u] הקטן ביותר (מבין אלה שבpq). נעדכן את ערכי שכניו בMin-Costs.

דוגמה:

עבור הגרף שראינו לעיל, וצומת המוצא $\displaystyle s = 1$ , הנה המצב ההתחלתי:

מבין כל הצמתים בpq, לצומת 1 ערך Min-Costs המינימאלי. נוציא אותו, לכן, ונעדכן את שכניו:

מבין כל הצמתים בpq, לצומת 2 ערך Min-Costs המינימאלי. נוציא אותו, לכן, ונעדכן את שכניו:

נמשיך כך הלאה עד שpq יתרוקן.

[עריכה] פסוודו-קוד

להלן הפסוודו-קוד לאלגוריתם Dijkstra:

Dijkstra(G, Edge-Costs, s)
1	pq = Make-Priority-Queue()
 
2	Min-Costs = Make-Array( Length(V(G)) )
 
3	for u in V(G)
4		Min-Costs[u] = u == s? 0 : ∞
5		Insert(pq, u)
 
6	while Size(pq) > 0
7		u = Delete-Min(pq)
 
8		for v in A(g, u)
9			if Min-Costs[v] > Min-Costs[u] + Edge-Costs[ (u, v) ]
10				Min-Costs[v] = Min-Costs[u] + Edge-Costs[ (u, v) ]
11				Decrease-Key(pq, v)
 
12	return Min-Costs

ולהלן דוגמה לשימוש בו:

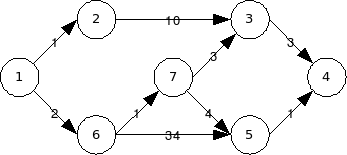
1	Min-Costs = Dijkstra(G, Edge-Costs, 1)
 
	# Prints 0.
2	Print( Min-Costs[1] )
 
	# Prints 6.
3	Print( Min-Costs[3] )

הנה הסבר לDijkstra:

ב1 מייצרים את את תור הקדימויות pq, וב2 מייצרים את את המערך Min-Costs.
הלולאה 6-11 פועלת כל עוד pq אינו ריק.
7 מוציאה את האיבר הקטן בpq (עפ"י קריטריון ההשוואה שהזכרנו), ו-8-11 מעדכנת את שכניו.
11 מעדכנת את pq שערך אחד מאיבריו ירד.

שימו לב:

קריטריון ההשוואה של pq הוא הערך של Min-Costs. כלומר, מבחינת pq, האיבר u נחשב קטן מהאיבר v אמ"ם Min-Costs[u] < Min-Costs[v].
בתורי קדימויות במימוש ערימה בינארית שראינו, שינוי חיצוני של ערך אחד מאיברי תור הקדימויות הוא הרסני. הפעולה Decrease-Key מתקנת מצב זה, אלא שלא ראינו פעולה כזו במימוש שראינו. אנו נניח שפעולה זו קיימת, ושסיבוכיותה לוגריתמית.

[עריכה] נכונות

משפט:

ב12, Min-Costs מכיל את הערכים הנכונים.

ההוכחה היא באינדוקציה על הטענות הבאות:

משפט:

בתחילת האיטרציה ה $\displaystyle i$ של 6-11:

לכל צומת v, אם Min-Costs[v] < ∞, אז יש מסלול במחיר Min-Costs[v] מs לv.
אם v הוא הצומת הקטן ביותר בpq (במובן שMin-Costs[v] הוא הקטן), אז אין מסלול מs ל $\displaystyle v$ שמחירו קטן יותר (ממש) מMin-Costs[v].

הוכחה: (בסיס האינדוקציה) בתחילת האיטרציה הראשונה Min-Costs[s] == 0,‏ בעוד שלכל $\displaystyle v \ne s$ ,‏ Min-Costs[v] > 0. מכאן גם ברור שs הוא הצומת הקטן ביותר. ברור שיש מסלול מs לעצמו במחיר 0, וגם ברור שאין מסלול זול יותר מ0 (כי מחירי כל הקשתות חיוביים).

(מעבר האינדוקציה) נניח שהטענות נכונות בתחילת האיטרציה ה $\displaystyle i$ , ונראה שהן נכונות בסוף האיטרציה ה $\displaystyle i$ .

נניח שטענה 1 אינה נכונה, דהיינו שאין מסלול מs לv כלשהו שעלותו Min-Costs[v] < ∞. נגדיר כ $\displaystyle j < i$ את האיטרציה האחרונה שבה שונה Min-Costs[v] (ב10). עפ"י הנחת האינדוקציה, באיטרציה $\displaystyle j$ אכן יש מסלול מs לu במחיר Min-Costs[u] (כפי שהיה ערכו באיטרציה $\displaystyle j$ ), אבל עפ"י זאת, 10 קובעת את Min-Costs[v] למחיר מסלול אפשרי - המסלול מs לu שבסופו משורשרת קשת מu לv.

נניח שטענה 2 איננה נכונה, דהיינו שיש מסלול זול יותר מMin-Costs[v]. נגדיר מסלול זה כ $\displaystyle u_1 \rightarrow ...\rightarrow u_j$ (עבור $\displaystyle j$ כלשהו).

נשים לב לאבחנות הפשוטות הבאות:

$\displaystyle u_1 = s \notin pq$
$\displaystyle u_j = v \in pq$
המסלול הזול ביותר מ $\displaystyle s$ לכל $\displaystyle u_1, ..., u_{j - 1}$ זול יותר מהמסלול הזול ביותר מ $\displaystyle s$ ל $\displaystyle v$ (למה?).

מהאבחנה הפשוטה הראשונה, ברור שיש צומת במסלול שאינו בpq אך הצומת שאחריו במסלול כן בpq (אם לא, כיצד ייתכן ש $\displaystyle s$ אינו בpq אך $\displaystyle u_j$ כן?). יש שתי אפשרויות:

באפשרות הראשונה, $\displaystyle u_1, \ldots, u_{j - 1} \notin pq$ ,‏ $\displaystyle u_j \in pq$ (כלומר, רק $\displaystyle v$ בתור הקדימויות).

נניח שזה המצב. מהנחת האינדוקציה, היות ש $\displaystyle u_{j - 1}$ כבר לא בתור הקדימויות, אז יש לו המחיר הנכון שלו. אך אם זה המצב, אז 10 בהכרח תקבע את ערכו של Min-Costs[v] למשהו שאינו גבוה ממחיר המסלול הזול ביותר מ $\displaystyle s$ אליו. זה סותר את את קביעתנו שטענה 2 איננה נכונה.

באפשרות השניה, נגדיר את $\displaystyle j'$ כך ש $\displaystyle u_{j' + 1}$ הוא הצומת הראשון במסלול שבpq (כלומר, $\displaystyle u_1, \ldots, u_{j'} \notin pq$ ).

נניח שזה המצב. מהנחת האינדוקציה, היותר ש $\displaystyle u_{j' - 1}$ כבר לא בתור הקדימויות, אז אז יש לו המחיר הנכון שלו. אך אם זה המצב, אז 10 בהכרח קבעה את מחירו למשהו זול יותר מאשר המחיר של $\displaystyle .$ זה סותר את הנחתנו ש $\displaystyle v$ הוא הצומת הזול ביותר בתור הקדימויות.

[עריכה] ניתוח סיבוכיות

נניח שהגרף נתון ברשימת שכנויות. 1-2 פועלות בבירור בזמן $\displaystyle \Theta(|V|)$ . 3-5 מבצעת $\displaystyle |V|$ פעולות Insert, ולכן אורכות זמן $\displaystyle \Theta(|V| \cdot \log(|V|))$ במקרה הגרוע. 6-11 מבצעות $\displaystyle |V|$ פעולות Delete-Min, ולכל היותר $\displaystyle |E|$ פעולות Decrease-Key (שעפ"י הנחתנו, סיבוכיותה לוגאריתמית), ולכן הן פועלות בזמן $\displaystyle \Theta((|V| + |E|) \cdot \log(|V|))$ במקרה הגרוע. הסיבוכיות, לכן, היא $\displaystyle \Theta((|V| + |E|) \cdot \log(|V|))$ במקרה הגרוע.