מבני נתונים ואלגוריתמים - מחברת קורס/שיעורי בית 4/שאלות

שימו לב: *נא להגיש רק את שאלות 1-5. שאר השאלות הן לצורך חזרה למבחן בלבד. אין צורך להגיש את התשובות להן.

1

בתכנית מסוימת רוצים לקלוט מספר רב של תווים מהמשתמש ולאחסנם. ביתר פירוט: רוצים לקרוא תו-תו מהמקלדת, עד שנלחץ התו 'q', ולשמור כל תו במבנה נתונים כלשהו. הבעיה היא שמספר התווים אינו ידוע מראש.

שלוש אפשרויות נבחנות. עבור כל אחד מהפתרונות, אנא אנא מצא את סדר הגדילה שלו, והסבר במילים מתי תשתמש בו (אם בכלל).

א'

שימוש ברשימה מקושרת:

1	l = Make-List()
	
2	do
3		c = Read()
4		if c != 'q'
5			Insert-Back(l, c)
6	while c != 'q'

הקוד פשוט למדי. 1 מייצרת רשימה מקושרת. הלולאה 2-6 קוראת תווים כל עוד לא נלחץ 'q', ומכניסה תווים (למעט 'q') לסוף הרשימה.

ב'

שימוש במערך גדל ב1:

1	A = Make-Array(1)
2	used = 0
	
3	do
4		c = Read()
5		if c != 'q'
6			A[++used] = c
			
7			if used == Length(A)
8				Tmp = Make-Array(used + 1)
				
9				for j in [1, ..., used]
10					Tmp[j] = A[j]
	
11				A = Tmp
12	while c != 'q'

1 מייצרת מערך בגודל 1.‏ 2 מאתחלת משתנה used, המתאר כמה איברים בשימוש בְמערך A,‏ ל1.‏ 3-12 קוראת תווים כל עוד לא נלחץ 'q', ומכניסה תווים (למעט 'q') לסוף המערך. 7-11 מטפלות במקרה בו נגמר המקום במערך A.‏ 8 מייצרת מערך חדש Tmp, שארכו גדול ב1 מזה של A.‏ 9-10 מעתיקות את האיברים למערך החדש. 11 משימה את המערך החדש לA במקום הקודם. ביציאה מהלולאה, A[1, ..., used] יחזיק את האיברים שנקלטו.

ג'

שימוש במערך גדל פי 2:

1	A = Make-Array(1)
2	used = 0
	
3	do
4		c = Read()
5		if c != 'q'
6			A[++used] = c
			
7			if used == Length(A)
8				Tmp = Make-Array(used * 2)
				
9				for j in [1, ..., used]
10					Tmp[j] = A[j]
	
11				A = Tmp
12	while c != 'q'

שים לב להבדל בין פתרון זה לפתרון הקודם. 8 אינה מגדילה את המערך החדש ב1 כמקודם, אלא פי 2.

2

א'

אנא כתוב מימוש יעיל לפונקציה List-Set-All(l, v) המקבלת (מצביע ל)רשימה מקושרת l, ערך v, וקובעת את הערכים בכל חוליות הרשימה לv.

ב'

אנא כתוב מימוש יעיל לפונקציה List-Union(l1, l2) המקבלת (מצביעים ל)רשימות מקושרות 1l וl2. לאחר הקריאה לפונקציה, על 1l להכיל את איחוד האיברים שהיו בשתי הרשימות לפני הקריאה, ועל l2 להיות ריקה.

3

להלן מבנה אפשרי לרשימה מקושרת חד-כוונית.

הרשימה מורכבת מחוליות. כל חוליה נראית כך:

# A data structure that describes a link which has a value, and can
#	be connected to a following and previous link.
Link
	# The next Link.
1	next
	# The value at this link.
2	value

להלן הפסוודו-קוד לרשימה עצמה:

# A data structure that describes a (doubly-linked) list of values.
List
        # The leftmost link.
1      front
        # The size (number of links).
2      size

(שימו לב שזה כמובן אינו המבנה היחידי האפשרי לרשימה מקושרת חד-כוונית: ייתכנו מימושים אחרים בעלי שדות עם שמות ומשמעויות שונים מעט.)

אנא הצע אלגוריתם בסיבוכיות $\displaystyle O(n)$ ובעל דרישת זיכרון קבועה (כלומר, שאינה גדלה עם $\displaystyle n$), ההופכת את סדר הרשימה (האיבר הראשון ייהפוך להיות האיבר האחרון, האיבר השני ייהפוך להיות האיבר לפני אחרון, וכולי).

4

הגדרה: מחרוזת היא רצף של תווים. אם $\displaystyle X=x_{1}\ldots x_{m}$,‏ $\displaystyle Y=y_{1}\ldots y_{n}$,‏ ו$\displaystyle Z=z_{1}\ldots z_{k}$ הן שלוש מחרוזות, אז: $\displaystyle Z$ היא תת-מחרוזת של $\displaystyle X$ אם קיימת סדרה עולה ממש של אינדקסים $\displaystyle i_{1},\ldots ,i_{k}$ כך ש$\displaystyle x_{i_{j}}=z_{j}$ לכל $\displaystyle j$. $\displaystyle Z$ היא תת-מחרוזת משותפת של $\displaystyle X$ ו$\displaystyle Y$ אם היא תת-מחרוזת הן של $\displaystyle X$ והן של $\displaystyle Y$

דוגמה: $\displaystyle Hello$ ו$\displaystyle ABCBDAB$ הן מחרוזות. אם $\displaystyle X=ABCBDAB$ ו$\displaystyle Y=BDCABA$, אז: אם נקבע $\displaystyle Z=BCBA$, אז $\displaystyle Z$ היא תת-מחרוזת של $\displaystyle X$. גם אם נקבע $\displaystyle Z=ABCBDAB$ (כלומר $\displaystyle X$ עצמה), אז $\displaystyle Z$ היא תת-מחרוזת של $\displaystyle X$. אם $\displaystyle X=ABCBDAB$ ו$\displaystyle Y=BDCABA$, אז $\displaystyle Z=BCBA$ היא תת-מחרוזת משותפת ל$\displaystyle X$ ול$\displaystyle Y$ (מבין כמה תתי-מחרוזות אפשריות).

הגדרה: אם $\displaystyle X$ ו$\displaystyle Y$ הן מחרוזות, אז $\displaystyle Z$ היא הLCS (או longest common subsequence), אם היא הארוכה ביותר מבין תתי-המחרוזות המשותפות ל$\displaystyle X$ ול$\displaystyle Y$.

בשאלה זו עליך למצוא אלגוריתם יעיל למציאת הLCS לכל שתי מחרוזות $\displaystyle X$ ו$\displaystyle Y$:

1. אנא תאר אלגוריתם יעיל המוצא את אורך הLCS.
2. אנא תאר אלגוריתם יעיל המדפיס את הLCS עצמו.

שימו לב: בכל אחד משני הסעיפים: הנח שX וY הם שני מערכים גלובליים המתארים את המחרוזות $\displaystyle X$ ו$\displaystyle Y$, בעלות האורכים $\displaystyle m$ ו$\displaystyle n$ בהתאמה. אנא הוכח נכונות תשובתך, ונתח את סיבוכיותה במונחי $\displaystyle m$ ו$\displaystyle n$.

5

נתונה פיסת בד שמידותיה $\displaystyle (n,m)$ (כלומר ארכה $\displaystyle n$ מטר, ורחבה $\displaystyle m$ מטר). הנח ש$\displaystyle n$ ו$\displaystyle m$ מספרים שלמים.

נתונות $\displaystyle k$ מידות, $\displaystyle (n_{1},m_{1}),...,(n_{k},m_{k})$, שלהן מותאמים מחירים $\displaystyle p_{1},...,p_{k}$. כלומר:

1. חתיכת בד במידה $\displaystyle (n_{1},m_{1})$ שווה $\displaystyle p_{1}$ שקלים.
2. חתיכת בד במידה $\displaystyle (n_{2},m_{2})$ שווה $\displaystyle p_{2}$ שקלים.
3. ...
4. חתיכת בד במידה $\displaystyle (n_{k},m_{k})$ שווה $\displaystyle p_{k}$ שקלים.חוץ מ$\displaystyle k$ מידות אלה, כל המידות האחרות חסרות ביקוש, ולכן כל חתיכת בד במידה שונה

ממידות אלה שווה 0 שקלים. הנח שכל $\displaystyle n_{i}$ ו$\displaystyle m_{i}$ הוא מספר שלם חיובי ממש.

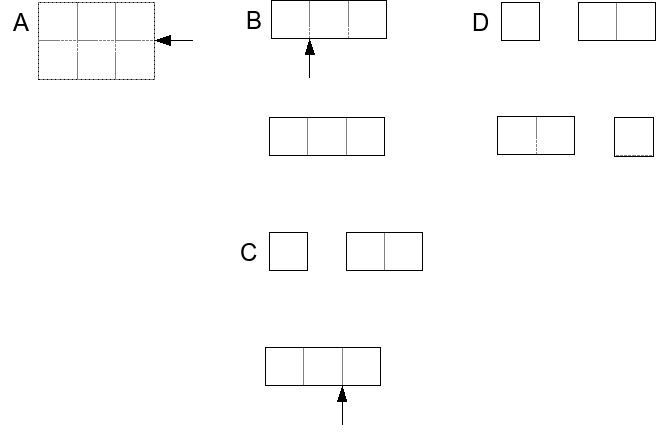
דוגמה: בתרשים הבא, A מראה פיסת בד במידות $\displaystyle (2,3)$, וB מראה שתי מידות בעלת ערך: העליונה בעלת המידות $\displaystyle (3,2)$, והתחתונה בעלת המידות $\displaystyle (1,2)$. נניח שהמידה העליונה שווה 35 שקל, והתחתונה שווה 2 שקלים. .

המטרה היא להפיק מהבד את מרב הערך, ע"י גזירת הבד אם יש תועלת בכך. בכל גזירה אפשר מותר לגזור את פיסת הבד לאורך או לרוחב. הנח שאין יכולת לסובב את פיסת הבד.

דוגמה: כיצד נוכל להשתמש בפיסת הבד מA שבדוגמה הקודמת? לו היינו יכולים לסובב אותה, היינו יכולים להפיק ממנה צורה ששווייה 35 שקל ללא גזירה אחת. עם זאת, עדיין יש סדרת גזירות שתפיק צורות בשווי 4 שקלים. בתרשים הבא: A מראה את החתך הראשון: נחתוך את הצורה אנכית בשורה 1, ונקבל את שתי הצורות בB. את הצורה העליונה בB נחתוך אנכית בטור הראשון, ונקבל את שלוש הצורות בC. את הצורה התחתונה בC נחתוך אנכית בטור 2, ונקבל את ארבע הצורות בD. כל אחת מהשורות בD מכילה כעת צורה אחת ששווייה 2 שקלים, ועוד צורה חסרת ערך. . יש עוד סדרות חיתוך שיניבו צורות בשווי 4 שקלים, אך אין סדרה שתניב יותר מכך.

בשאלה זו עליך למצוא אלגוריתם יעיל למציאת סדרת החיתוך הרווחית ביותר. אנא הוכח שהאלגוריתם שמצאת עובד בסיבוכיות $\displaystyle O(n\cdot m\cdot (n+m))$.

הנח שקיימת פונקציה Value(i, j) המחזירה בזמן $\displaystyle O(1)$:

1. 0 אם $\displaystyle (i,j)$ אינה אחת מ$\displaystyle k$ המידות בעלות התועלת.
2. $\displaystyle p_{k}$ אם $\displaystyle (i,j)=(n_{k},m_{k})$.

כדאי לדעת: אפשר לפתור את הבעיה בצורה הבאה. מכינים טבלה בגודל $\displaystyle m$ על $\displaystyle n$ ובתא ה- $\displaystyle (i,j)$ שמים את הרווח מחיתוך הבד לגודל $\displaystyle (i,j)$. רווח זה יהיה המקסימום מהרווחים אותם אפשר להשיג מחיתוך הבד לרוחב, מחיתוך הבד לאורך, וממכירת הבד כפי שהוא (כפי שמוחזר מהפונקציה Value(i, j)).

6

אנא הצע מימוש לתור בעזרת שתי מחסניות, כך שאם סך מספר הפעולות על התור הוא $\displaystyle n$, אז סדרת הפעולות תעבוד בזמן $\displaystyle \Theta (n)$.

7

אנא כתוב מימוש יעיל לפונקציה Find-Num-In-Range(A, a, b), המקבלת:

1. מערך A של מספרים מרוכבים לאו דווקא שלמים, הממויין לפי מרחק המספרים מראשית הצירים
2. מספר ממשי לאו דווקא שלם $\displaystyle a$
3. מספר ממשי לאו דווקא שלם $\displaystyle b$

ומחזירה את מספר האיברים בA שמרחק כל אחד מהם מראשית הצירים נמצא בתחום $\displaystyle [a,b)$.

הנח שברשותך פונקציה Dist(x) המקבלת מספר מרוכב ומחזירה את מרחקו מראשית הצירים.