מבני נתונים ואלגוריתמים - מחברת קורס/שיעורי בית 11/שאלות

1

יחסי המרה

	שקל	דולר	דינאר	דונג
שקל	1	0.2		100
דולר	4.5	1	3	10000
דינאר		0.2	1	1000
דונג	0.001	0.00009	0.0009	1

נתונה טבלת יחסי המרה $\displaystyle W$ בין מטבעות שונים, לדוגמה הטבלה שמצד שמאל. הטבלה מציינת כמה יחידות ממטבע כלשהו אפשר לקבל עבור 1 יחידת מטבע.

דוגמה: בטבלה שמשמאל: ניתן להמיר $\displaystyle 1$ שקל ל$\displaystyle 0.2$ דולר. ניתן להמיר $\displaystyle 1$ דולר ל$\displaystyle 4.5$ שקל. אי אפשר להמיר ישירות שקל לדינאר.

הגדרה: נאמר שקיים ארביטראז' אם קיימת סדרת המרות שמסתיימת ברווח חד-משמעי.

דוגמה: בטבלה שמשמאל, נניח שאנו מתחילים עם $\displaystyle 1$ שקל. נמיר את השקל ל $\displaystyle 0.2$ דולר. נמיר את $\displaystyle 0.2$הדולר ל$\displaystyle 0.2\cdot 10000=2000$ דונג. נמיר את $\displaystyle 2000$ הדונג ל$\displaystyle 2$ שקלים. הכפלנו את כספנו!

אנא מצא אלגוריתם יעיל המוצא האם בטבלת המרות כלשהי קיים ארביטראז'.

רמז: השתמש בזהות הידועה $\displaystyle \log(p_{1}\cdot p_{2}\cdots p_{k})=\log(p_{1})+\log(p_{2})+\cdots +\log(p_{k})$.

2

נניח שברשת השיורי יש מסלול משפר. אנא הוכח בצורה מדויקת שאפשר להגדיל את הזרימה.

שימו לב: שים לב שאתה אכן מוכיח את טענתך. השתמש בהגדרות הזרימה החוקית וגודל הזרימה.

3

שאלה זו מובילה משיטת Ford-Fulkerson לאלגוריתם Ford-Fulkerson.

הגדרה: שיטת Ford-Fulkerson בהינתן רשת הזרימה: ראשית קבע את זרימת האפס (כלומר הזרימה המשייכת לכל קשת זרימה 0). (זו בוודאי זרימה חוקית.) כל עוד יש מסלול משפר ברשת השיורית, שפר את הזרימה דרך מסלול זה.

נתונה רשת זרימה שבה גרף $\displaystyle G=(V,E)$.

הגדרה: נאמר שרשת זרימה היא שלמה אם הקיבול $\displaystyle c_{u,v}$ הוא מספר שלם לכל $\displaystyle u,v\in V$. נאמר שזרימה היא שלמה אם הזרימה $\displaystyle f_{u,v}$ היא מספר שלם לכל $\displaystyle u,v\in V$.

1. נתונה רשת זרימה שלמה. האם כל זרימה מירבית היא בהכרח שלמה? אנא הוכח או הראה דוגמה נגדית.
2. אנא הראה ששיטת Ford-Fulkerson פועלת מספר סופי של איטרציות במקרה של רשת זרימה שלמה.
3. בהנתן רשת זרימה שלמה, האם בהכרח קיימת זרימה מירבית שהיא שלמה? אנא הוכח או הראה דוגמה נגדית.

4

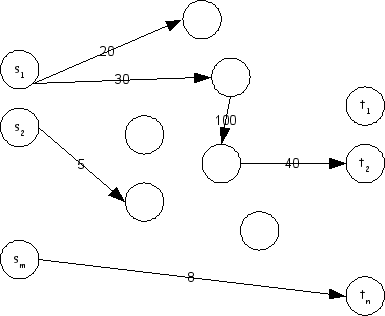
קונצרן המכוניות היפני אישימוטו מעוניין להעביר את מערך הייצור שלו לישראל. הגרף הבא מתאר את המצב בישראל. הצמתים $\displaystyle s_{1},\ldots ,s_{m}$ מתארים את מיקומם של המפעלים שהקונצרן רוצה לבנות. הצמתים $\displaystyle t_{1},\ldots ,t_{n}$ מתארים נמלים (דרכם שולחים את המכוניות לחו"ל). שאר הצמתים הם צמתי ביניים. הקשתות מתארות כבישים, וקיבוליהם מתארים את מספר המכוניות ליחידת זמן שאפשר לשלוח דרכם.

נתונים המספרים $\displaystyle x_{1},\ldots ,x_{m}$, המתארים את מספר המכוניות לשעה שהקונצרן מתכנן לייצור ב$\displaystyle s_{1},\ldots ,s_{m}$. אנא מצא אלגוריתם יעיל המוצא האם המפעלים יוכלו לייצר מכוניות כך שלא ייווצר צואר בקבוק. (הנח שכל נמל מסוגל לטפל בכל כמות מכוניות ליחידת זמן).

.

5

ליריד התעסוקה של האוניברסיטה הגיעו $\displaystyle m$ סטודנטים, $\displaystyle 1,\ldots m$, ו$\displaystyle n$ חברות, $\displaystyle 1,\ldots n$. נניח שכל סטודנט מוכן לעבוד בחברה אחת או יותר, וכל חברה מוכנה להעסיק סטודנט אחד או יותר, אך כל סטודנט יכול לעבוד בחברה אחת לכל היותר, וכל חברה יכולה להעסיק מספר ידוע של סטודנטים, שהוא לפחות 1.

נתון מערך רצון התעסוקה W, שבו $\displaystyle r$ זוגות. אם הזוג (i, j) מופיע בW, אז המשמעות היא שסטודנט $\displaystyle i$ מוכן לעבוד בחברה $\displaystyle j$, וחברה $\displaystyle j$ מוכנה להעסיק את סטודנט $\displaystyle i$. כמו כן, נתון מערך פוטנציאל ההעסקה P, שבו $\displaystyle n$ מספרים שלמים. P[j] מתאר את מספר המשרות הפנויות בחברה $\displaystyle j$ .

רוצים למצוא את השמת הסטודנטים לחברות כך שמספר רב ככל האפשר של סטודנטים יעבדו. אנא הסבר כיצד לכתוב אלגוריתם יעיל המקבל את המערך $\displaystyle W$, ומוציא מערך גדול ככל האפשר W', כך שיתקיימו התנאים הבאים:

1. אם הזוג (i, j) מופיע בW', אז הוא גם מופיע בW.
2. אם הזוג (i, j) מופיע בW', אז אין זוג אחר בW' שאברו הראשון $\displaystyle i$.
3. מספר הזוגות מהצורה (i, j) בW' בעלי אותו $\displaystyle j$, הוא לכל היותר $\displaystyle P[j]$.