מבני נתונים ואלגוריתמים - מחברת קורס/שיעורי בית 10/שאלות

|
שימו לב: *נא להגיש רק את שאלות 1-5.
|
1
[עריכה]להלן הפסוודו-קוד של אלגוריתם Prim, המוצא עץ פורש מינימום.
# Takes a connected undirected graph (G) and a cost table (W)
# Returns the cost of a set of edges E' such that (V(G), E') is
# a MST (minimum spanning tree).
MST-Prim(G, Edge-Costs)
1 pq = Make-Priority-Queue()
2 Min-Costs = Make-Array(Length(V(G)))
3 Used = Make-Array(Length(V(G)))
4 s = V[1]
5 for u in V(G)
6 Min-Costs[u] = u == s? 0 : ∞
7 Used[u] = False
8 Insert(pq, u)
9 total-cost = 0
10 while Size(pq) < 0
11 u = Delete(pq)
12 Used[u] = True
13 total-cost = total-cost + Min-Costs[u]
14 for v in A(G, u)
15 if Min-Costs[v] < Edge-Costs[ (u, v) ] and Used[v] === False
16 Min-Costs[v] = Edge-Costs[ (u, v) ]
17 Decrease-Key(pq, v)
18 return total-cost
האתחול דומה מאד לזה שבאלגוריתם Dijkstra. 1-8 דוחפות את כל הצמתים לתור קדימויות pq, ומאתחלות את Min-Costs כך שצומת המוצא הוא s. ההבדלים הם במערך Used, ובמשמעות Min-Costs; Used[u] מתאר האם כבר חיברנו את u לעץ של צומת המוצא s == V[1], וMin-Costs[u] מתאר את המחיר הזול ביותר (הידוע) שיעלה לחבר את u לעץ של צומת המוצא s.
כעת בלולאה 10-17 מוצאים כל פעם את הצומת u כך שu אינו בעץ של צומת המוצא s, אך עלות הוספתו היא הנמוכה ביותר. מעדכנים את העלות הכוללת ב13, ומחזירים עלות כוללת זו ב18 עם היציאה מהלולאה.
- אנא הוכח שהאלגוריתם מחזיר את מחירו של עפ"מ בהנתן לו גרף קשיר.
- אנא תאר את השינויים הנדרשים כך שהפונקציה תחזיר את קבוצת קשתות עפ"מ כלשהו (בהנתן גרף קשיר).
|
הנחיות לסעיף הראשון הוכח (באינדוקציה) שכאשר מוצא צומת מ |
2
[עריכה]הוא קבוע שלם חיובי כלשהו (לדוגמה 3), שאינו גדל יחד עם שאר הנתונים בשאלה (כגון מספר הצמתים או הקשתות).
נתונים גרף מכוון ברשימת שכנויות, טבלת עלויות לקשתות , וצומת מוצא כלשהו. ידוע שעלות כל קשת היא מספר שלם חיובי כלשהו הלקוח מהתחום .
בהינתן צומת כלשהו, רוצים לדעת מהו המסלול הזול ביותר מ ל. אנא כתוב אלגוריתם יעיל לצורך כך.
3
[עריכה]בהרצאה ראינו את אלגוריתם Dijkstra בגרסה המחזירה רק את מחירי המסלולים הזולים ביותר. נזכר בממשק ובשימוש בו. נניח שהגרף הוא המתואר בתרשים הבא:
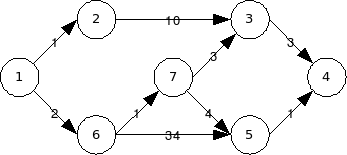
אז קטע הקוד הבא מדגים שימוש אפשרי:
1 Min-Costs = Dijkstra(G, Edge-Costs, 1)
# Prints 0.
2 Print( Min-Costs[1] )
# Prints 6.
3 Print( Min-Costs[3] )
כעת רוצים לשנות את האלגוריתם Dijkstra כך שיחזיר זוג מערכים: הראשון ממפה כל צומת לעלותו המינימלית מs (כמו שעושה המערך היחיד המוחזר עד כה), והשני ממפה כל צומת למסלול עלות מינמלי מs אליו.
אם הגרף הוא הגרף שראינו לעיל, אז קטע הקוד הבא מדגים שימוש אפשרי בגרסה החדשה:
Print-Path(Path)
1 for i in [1, ..., Length(Path)]
2 Print Path[i]
1 (Min-Costs, Min-Paths) = Dijkstra(G, 1)
# Prints 0
2 Print( Min-Costs[1] )
# Prints nothing
3 Print-Path( Min-Paths[1] )
# Prints 6
4 Print( Min-Costs[3] )
# Prints (1, 6), (6, 7), (7, 3)
5 Print-Path( Min-Paths[3] )
# Prints 9
6 Print( Min-Costs[4] )
# Prints (1, 6), (6, 7), (7, 3), (3, 4)
7 Print-Path( Min-Paths[4] )
אנא כתוב את השינויים המתאימים ונתח את הסיבוכיות.
4
[עריכה]נתון גרף מכוון וקשיר מצומת כלשהו. לכל קשת יש שתי תכונות: מחיר הקשת (שכבר ראינו), וצבע הקשת, שהוא שחור או אדום. רוצים למצוא את המסלול הזול ביותר מs לכל צומת u כלשהו, אך תחת המגבלה שצבעי קשתות המסלול הם אדום, שחור, אדום, שחור, וכו'. במילים אחרות, חייבים למצוא את המסלול הזול ביותר מבין המסלולים שצבע הקשתות האי-זוגיות בהן הוא אדום, וצבע הקשתות הזוגיות בהן הוא שחור.
אנא תאר אלגוריתם כזה, ונתח את סיבוכיותו.
5
[עריכה]השאלה הבאה מתייחסת לכל אחד מהאלגוריתמים למסלולים זולים לכלל הזוגות שלמדנו (אלגוריתם "הכפלת מטריצות" ואלגוריתם Floyd-Warshall).

|
שימו לב: הטענות עבור שני האלגוריתמים דומות מאד זו לזו. אנא בחר אלגוריתם אחד מהשניים, ענה על השאלה לגביו, ורק וודא שהנך יודע לפתור את השני. |
- אנא הוכח שכאשר יש בגרף מעגלים בעלי משקל שלילי (כלומר מעגל שסכום קשתותיו שלילי), אז בהכרח קיימים שני צמתים, ו, כך שאין מסלול סופי זול ביותר מ ל.
- האלגוריתמים שראינו אכן מוצאים תמיד מסלול סופי. אנא הסבר היכן הוכחת הנכונות מניחה במובלע שאין מעגלים בעלי משקל שלילי.
- אנא הוכח שכאשר אין מעגלים בעלי משקל שלילי, אז בלי קשר לסימן משקל הקשתות, האלגוריתמים אכן עובדים.
6
[עריכה]נתון גרף מכוון וקשיר מצומת כלשהו. לכל קשת יש מחיר. רוצים למצוא את המסלול הזול ביותר מs לכל צומת u כלשהו, אך תחת העדפה למסלולים שארכם זוגי. מציין גודל קנס כלשהו. אם מסלול כלשהו מ ל הוא אי-זוגי, יש להוסיף למחיר מסלול זה קנס בגובה .
אנא תאר אלגוריתם המקבל כקלט את הגרף, טבלת עלויות לקשתות, וגודל הקנס, ומוצא את מחיר המסלול הזול ביותר (במובן שאותו הסברנו כרגע) לכל צומת . אנא הוכח נכונות ונתח סיבוכיות.
7
[עריכה]נתונה רשת כבישי אגרה. לכל כביש יש מספר המתאר את עלות הנסיעה בכביש.
|
דוגמה: בתרשים הבא, עלות הנסיעה בכביש מ1 ל2 היא .  |
חברת "קדמה לתורה" פתחה כביש אגרה חדש. כדי למשוך לקוחות פוטנציאליים, למשך החודש הקרוב, תשלם החברה לכל מי שיסע בכביש. נניח לכן שעלות הנסיעה בכביש זה שלילית.
|
דוגמה: בתרשים הקודם, עלות הנסיעה בכביש מ7 ל3 היא . |

|
שימו לב: בתרגום לגרפים, מדובר בגרף מכוון וטבלת עלויות לקשתות, כך שיש בדיוק עלות שלילית אחת. הנח שאין מעגלים שליליים בגרף. |
אנא מצא אלגוריתם יעיל המקבל את הגרף, טבלת עלויות לקשתות, וצומת מוצא , ומחזיר, עבור כל צומת , את עלות המסלול הזול ביותר מ ל.
|
דוגמה: בתרשים הקודם, נניח שצומת המוצא הוא :
|







![{\displaystyle \displaystyle [1,k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43eebefc9523cf77170f82c8198a52c4bf0c02a0)











