מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/אלגוריתמי זרימה/תרגילים
קשת שיורית נעלמת ומופיעה
[עריכה]שאלה
[עריכה]נתונה רשת זרימה כלשהי. מנסים למצוא זרימה מירבית בעזרת שיטת Ford-Fulkerson. נזכר שהרשת השיורית משתנה בכל אירטציה.
אנא הוכח או הפרך את הטענה הבאה. אם באיטרציה i נעלמת הקשת מגרף הרשת השיורית, אז לא תופיע בגרפי הרשתות השיוריות באיטרציות לאחר .
תשובה
[עריכה]הטענה אינה נכונה.
נתבונן ברשת שבתרשים הבא:

הרשת השיורית זהה בשלב זה לרשת המקורית. נניח שמשפרים ראשית דרך המסלול . הרשת השיורית נראית כך:

שים לב שהקשת נעלמה מהרשת השיורית. נעלמה מהרשת השיורית. כעת נניח שמשפרית דרך המסלול . אז הרשת השיורית נראית כך:
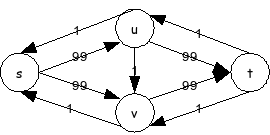
שים לב שהקשת חזרה לרשת השיורית.
זרימה מירבית בקיבולים מוגבלי שורש
[עריכה]שאלה
[עריכה]נתונה רשת זרימה שבה גרף . נתון שהחתך הקטן ביותר (מבחינת גודל הקיבול) הוא .
- נתון שכל אחד מקיבולי הרשת הוא מספר שלם. אנא הצע שיטה יעילה למציאת הזרימה המירבית.
- אנא חזור על הסעיף הקודם, אך עתה אל תניח שכל אחד מהקיבולים הוא מספר שלם.
תשובה
[עריכה]- נריץ את אלגוריתם Edmonds-Karp, אך ננתח אותו בצורה עדינה יותר, תוך לקיחה בחשבון שכל אחד מהקיבולים הוא מספר שלם, ושאנו יודעים את גודל קיבול החתך הקטן ביותר. עפ"י המשפט המשפט Max-Flow Min-Cut ונתוני השאלה, אנו יודעים שגודל הזרימה המירבית כאן הוא . מנתוני השאלה גם קל לראות שכל איטרציה משפרת את הזרימה בלפחות יחידה אחת. מכאן נובע שיש לכל היותר איטרציות. כל איטרציה מפעילה את אלגוריתם BFS, שבמקרה כאן יעבוד בזמן . הסיבוכיות הכללית, לכן, היא
- גם הפעם נריץ את אלגוריתם Edmonds-Karp, אך לא נוכל לחזור על הניתוח שבסעיף הקודם (מדוע?). כל שנוכל לטעון הוא שהסיבוכיות היא .
שיטת Ford-Fulkerson ברשת זרימה שלמה
[עריכה]שאלה
[עריכה]שאלה זו מובילה משיטת Ford-Fulkerson לאלגוריתם Ford-Fulkerson.
|
הגדרה: שיטת Ford-Fulkerson בהינתן רשת הזרימה:
|
נתונה רשת זרימה שבה גרף .
|
הגדרה:
|
- נתונה רשת זרימה שלמה. האם כל זרימה מירבית היא בהכרח שלמה? אנא הוכח או הראה דוגמה נגדית.
- אנא הראה ששיטת Ford-Fulkerson פועלת מספר סופי של איטרציות במקרה של רשת זרימה שלמה.
- בהנתן רשת זרימה שלמה, האם בהכרח קיימת זרימה מירבית שהיא שלמה? אנא הוכח או הראה דוגמה נגדית.
תשובה
[עריכה]1
[עריכה]התרשים הבא מראה דוגמה נגדית לטענה.

בגרף זה כל הקיבולים שלמים (כל אחד מהם הוא 1). הזרימות מתוארות בסוגריים, ולא כולן שלמות. קל לראות שהזרימה מירבית, מפני שגודל הזרימה (שהוא 1) הוא בדיוק גודל קיבול החתך בין 4 ל5.
2
[עריכה]נראה באינדוקציה ששיטת Ford-Fulkerson תזרים יחידות שלמות במקרה זה.
הוכחה: בכל איטרציה מוצאים מסלול משפר ברשת השיורית, ומשפרים דרכו. האינדוקציה היא על מספר האיטרציה.
(בסיס האינדוקציה) הרשת השיורית היא בתחילה רשת שלמה - קיבולי הקשתות חיוביים, והזרימה היא 0. לכן כל קיבול במסלול משפר הוא שלם. הזרימה המשפרת גם היא תהיה שלמה.
(מעבר האינדוקציה) נניח שכל הזרימות שלמות. אז שוב כל קיבול במסלול משפר הוא שלם - הקיבול השיורי הוא ההפרש בין הקיבול (שהוא שלם) לזרימה (שמהנחת האינדוקציה היא שלמה). הזרימה המשפרת גם היא תהיה שלמה.
היות שהזרימה היא שלמה, אז כל איטרציה של Ford-Fulkerson תשפר את הזרימה ב1 לפחות. מספר האיטרציות, לכן, חסום.
3
[עריכה]הטענה נכונה, והיא נובעת מהסעיף הקודם.
שיטת Ford-Fulkerson תפעל בזמן סופי במקרה זה, והיא תזרים זרימה שלמה. כשהשיטה עצרה את פעולתה, לא היה מסלול משפר ברשת השיורית. כבר למדנו שנובע מכך שהזרימה היא מירבית.
רשת זרימה שלמה
[עריכה]שאלה
[עריכה]נתונה רשת זרימה שבה גרף .
|
הגדרה:
|
אנא הוכח או הפרך כל אחת מהטענות הבאות.
- ברשת זרימה שלמה, תמיד קיימת זרימה מירבית שהיא שלמה.
- ברשת זרימה שלמה, כל זרימה מירבית היא שלמה.
- ברשת זרימה שלמה שכל אחד מקיבוליה קטן מ7, מספר האיטרציות של אלגוריתם Ford-Fulkerson הוא .
- ברשת זרימה, לאו דוקא שלמה, שכל אחד מקיבוליה קטן מ7, מספר האיטרציות של אלגוריתם Ford-Fulkerson הוא .
תשובה
[עריכה]1
[עריכה]הטענה נכונה.
נתבונן בהוכחה של אלגוריתם Ford-Fulkerson. ההוכחה מניחה שכל הקיבולים שלמים (כמו במקרה שלנו), ומגיעה למסקנה שבכל שיפור (כולל השיפור האחרון), הזרימות עדיין שלמות (מה שצריך להוכיח כאן).
2
[עריכה]הטענה אינה נכונה.
להלן דוגמה נגדית.

ברשת הזרימה הזו, קל מאד לראות שהזרימה המירבית בגודל 1.
להלן זרימה בגודל 1 שאינה זרימה שלמה:


|
שימו לב: הדוגמה הנגדית לסעיף זה אינה סותרת את הסעיף הקודם. אכן יש זרימה מירבית שהיא שלמה, כפי שהתרשים הבא מראה:
 |
3
[עריכה]הטענה נכונה.
נתבונן בחתך כלשהו בגרף. מספר הקשתות שחוצות אותו (מ ל) הוא לכל היותר . על פי נתוני השאלה, כל אחד מקיבולי הקשתות קטן מ7. לכן, קיבול החתך הוא לכל היותר . היות שהדבר נכון לכל חתך, הוא נכון גם לחתך הקטן ביותר (מבחינת גודל הקיבול). לכן, עפ"ׁי המשפט Max-Flow Min-Cut, גודל הזרימה המירבית הוא לכל היותר . היות שכל אחד מקיבולי הקשתות הוא מספר שלם, אז כל איטרציה של אלגוריתם ford-Fulkerson תשפר את הזרימה בלפחות 1. מספר האיטרציות לכן הוא לכל היותר .
4
[עריכה]הטענה אינה נכונה.
להלן דוגמה נגדית. התרשים הבא מראה גרף רשת זרימה. הגרף מורכב למעשה משני גרפים זרים. הראשון מכיל 4 צמתים ו5 קשתות. הגרף מכיל עוד מספר צמתים וקשתות בעלי קיבולים שונים (שאינם מענייננו).
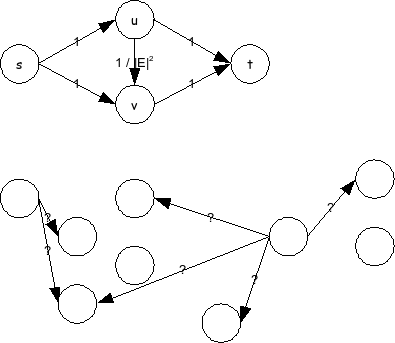
קל לראות שהזרימה המירבית בעלת גודל 2. להלן זרימה כזאת (מכאן ועד סוף השאלה לא נצייר את כל הצמתים והקשתות בגרף):

נניח שהמסלול המשפר הראשון שבחרנו הוא (ולכן הזרימה בסוף האיטרציה הראשונה היא בגודל ). התרשים הבא מראה את גרף הרשת השיורית בשלב זה.

מתרשים זה אפשר לראות שיש כעת שיפור שגם הוא בעל גודל :
השיפור דרך המסלול < math dir = "ltr">\displaystyle s \rightarrow v \rightarrow u \rightarrow t</math> (ולכן הזרימה בסוף האיטרציה השניה היא בגודל ).
קל להראות (פורמלית, באינדוקציה), שאפשר לבצע שיפורים (בזוגות), כך שכל שיפור אי-זוגי יהיה דרך , כל שיפור זוגי יהיה דרך , וגודל הזרימה יהיה .
היות שגודל הזרימה המירבית הוא 2, אז מספר האיטרציות הוא פתרון המשוואה , ולכן .
מערך הייצור בקונצרן אישימוטו
[עריכה]שאלה
[עריכה]קונצרן המכוניות היפני אישימוטו מעוניין להעביר את מערך הייצור שלו לישראל. הגרף הבא מתאר את המצב בישראל. הצמתים מתארים את מיקומם של המפעלים שהקונצרן רוצה לבנות. הצמתים מתארים נמלים (דרכם שולחים את המכוניות לחו"ל). שאר הצמתים הם צמתי ביניים. הקשתות מתארות כבישים, וקיבוליהם מתארים את מספר המכוניות ליחידת זמן שאפשר לשלוח דרכם.
נתונים המספרים , המתארים את מספר המכוניות לשעה שהקונצרן מתכנן לייצור ב. אנא מצא אלגוריתם יעיל המוצא האם המפעלים יוכלו לייצר מכוניות כך שלא ייווצר צואר בקבוק. (הנח שכל נמל מסוגל לטפל בכל כמות מכוניות ליחידת זמן).
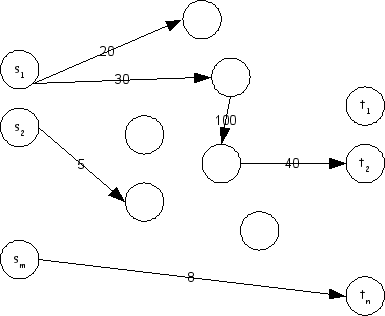
תשובה
[עריכה]ראשית נתרגם את השאלה לדרישות מדויקות מעט יותר. השאלה, למעשה, מבקשת לבדוק האם קיימת זרימה ברשת כך שיתקיימו הדברים הבאים:
- הזרימה היוצאת מ היא .
- מתקיימות הווריאציות הבאות של זרימה חוקית:
- (מגבלת הקיבול) הזרימה הישירה בין שני צמתים אינה עולה על הקיבול ביניהם; .
- (סימטריה הפכית) הזרימה הישירה מצומת לצומת היא מינוס הזרימה הישירה מצומת
לצומת ; .
- (שימור הזרם) בכל צומת, למעט (אולי) הצמתים ו, הצומת אינו אוגר או מייצר זרם; .(שים לב שרק הדרישה השלישית השתנתה.)
נבנה, לכן, גרף חדש. נוסיף בו שני צמתים ו, ועוד מספר קשתות. הגרף החדש מתואר להלן:

בגרף החדש, כל קשת מהצורה בעלת הקיבול , וכל קשת מהצורה בעלת הקיבול .
נבדוק בגרף החדש האם יש זרימה מלבגודל .
|
משפט: יש פתרון לבעיה החדשה \Leftrightarrow יש פתרון לבעיה המקורית. |
הוכחה: (⇐)
נניח שיש פתרון לבעיה החדשה (כלומר, אכן יש זרימה שגודלה ). נתבונן בחתך הבא:

מה נוכל לראות מחתך זה וממגבלות הזרימה? מצד אחד, גודל הזרימה כאן הוא
מצד שני, מגבלת קיבול החתך על זרימת החתך אומרת כי
מכאן קל לראות שבהכרח, לכל
,
יריד תעסוקה 1
[עריכה]שאלה
[עריכה]ליריד התעסוקה של האוניברסיטה הגיעו סטודנטים, , ו חברות, . נניח שכל סטודנט מוכן לעבוד בחברה אחת או יותר, וכל חברה מוכנה להעסיק סטודנט אחד או יותר, אך כל סטודנט יכול לעבוד בחברה אחת לכל היותר, וכל חברה יכולה להעסיק סטודנט אחד לכל היותר.
נתון מערך רצון התעסוקה W, שבו זוגות. אם הזוג (i, j) מופיע בW, אז המשמעות היא שסטודנט מוכן לעבוד בחברה , וחברה מוכנה להעסיק את סטודנט .
רוצים למצוא את השמת הסטודנטים לחברות כך שמספר רב ככל האפשר של סטודנטים יעבדו. אנא הסבר כיצד לכתוב אלגוריתם יעיל
המקבל את המערך , ומוציא מערך גדול ככל האפשר W', כך שיתקיימו התנאים הבאים:
- אם הזוג
(i, j)מופיע בW', אז הוא גם מופיע בW. - אם הזוג
(i, j)מופיע בW', אז אין זוג אחר בW'שאברו הראשון . - אם הזוג
(i, j)מופיע בW', אז אין זוג אחר בW'שאברו השני .
|
רמז בנה גרף שבו יש צומת לכל סטודנט, צומת לכל חברה, צומת , וצומת . חשוב מהן קשתות הגרף. חשוב איזו בעיית זרימה תפתור את הבעיה כאן. |
תשובה
[עריכה]ראשית נבנה את רשת הזרימה המתוארת בתרשים הבא. בגרף זה צמתים:
- צמתים , אחד לכל סטודנט
- צמתים , אחד לכל חברה
- צומת מקור וצומת בור
נגדיר כ את Length(W).
בגרף יש קשתות:
- קשת אחת לכל איבר ב
W - קשת מ לכל
- קשת מכל לקיבולי כל אחת מהקשתות הוא 1.

כעת נריץ את אלגוריתם Ford-Fulkerson. נחזיר כתשובה כל זוג שעבורו קיבלנו .
|
משפט: האלגוריתם מחזיר תשובה נכונה. |
הוכחה: אנו יודעים שאלגוריתם Ford-Fulkerson משפר תמיד בגדלים שלמים (שהרי הקיבולים שלמים). קל מאד להוכיח (פורמלית, באינדוקציה), שבמקרה זה, חלק מהקשתות יזרימו 1, והשאר 0 (אלו האפשרויות היחידות). נצייר את הגרף המתקבל ממחיקת הקשתות שאינן מזרימות כלום:
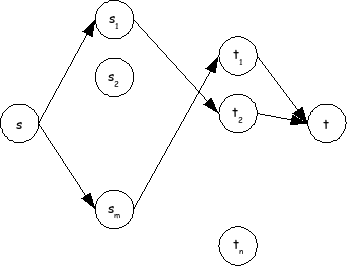
נניח שיש קשת בין ל. בהכרח הקשת מזרימה 1. מצד שני, הקשת המזרימה מ ל מזרימה גם היא 1. משימור הזרם נובע אם כן שאין קשת אחרת היוצאת מ. טענה כמעט זהה מראה שאין קשת אחרת הנכנסת ל. ברור גם שקשת זו היתה שייכת לגרף המקורי. מכאן נובע שהמערך המוחזר W' אכן משייך אחת לאחת סטודנט לחברה, ואינו ממציא שיוכים שלא הופיעו במקור.
נסמן כ את גודל W'. מניין לנו שאין התאמה גדולה יותר? נניח בשלילה שיש כזו, ונסמן את גודלה כ. אבל, מכאן נובע בהכרח (בסתירה לנכונות Ford-Fulkerson) שיש זרימה בגודל בגרף החדש: קל למצוא קשתות מ לצמתי הסטודנטים, ומצמתי החברות ל, ובדיקה פשוטה של חוקי הזרימה החוקית מראים שאם מזרימה יחידה 1 בכל אחת מקשתות אלו, אז זו אכן זרימה חוקית.
|
משפט: סיבוכיות האלגוריתם . |
הוכחה: אם משתמשים ברשימת שכנויות, אז בניית הגרף החדש היא .כבר ראינו בניתוח אלגוריתם Ford-Fulkerson, שסיבוכיותו לינארית במספר הקשתות כפול גודל הזרימה המירבית. מספר הקשתות כאן הוא , והזרימה המירבית היא
יריד תעסוקה 2
[עריכה]שאלה
[עריכה]ליריד התעסוקה של האוניברסיטה הגיעו סטודנטים, , ו חברות, . נניח שכל סטודנט מוכן לעבוד בחברה אחת או יותר, וכל חברה מוכנה להעסיק סטודנט אחד או יותר, אך כל סטודנט יכול לעבוד בחברה אחת לכל היותר, וכל חברה יכולה להעסיק מספר ידוע של סטודנטים, שהוא לפחות 1.
נתון מערך רצון התעסוקה W, שבו זוגות. אם הזוג (i, j) מופיע בW, אז המשמעות היא שסטודנט מוכן לעבוד בחברה , וחברה מוכנה להעסיק את סטודנט . כמו כן, נתון מערך פוטנציאל ההעסקה P, שבו מספרים שלמים. P[j] מתאר את מספר המשרות הפנויות בחברה .
רוצים למצוא את השמת הסטודנטים לחברות כך שמספר רב ככל האפשר של סטודנטים יעבדו. אנא הסבר כיצד לכתוב אלגוריתם יעיל המקבל את המערך , ומוציא מערך גדול ככל האפשר W', כך שיתקיימו התנאים הבאים:
- אם הזוג
(i, j)מופיע בW', אז הוא גם מופיע בW. - אם הזוג
(i, j)מופיע בW', אז אין זוג אחר בW'שאברו הראשון . - מספר הזוגות מהצורה
(i, j)בW'בעלי אותו , הוא לכל היותר .
תשובה
[עריכה]ראשית נבנה את רשת הזרימה המתוארת בתרשים הבא. בגרף זה צמתים:
- צמתים , אחד לכל סטודנט
- צמתים , אחד לכל חברה
- צומת מקור וצומת בור
נגדיר כ את Length(W).
בגרף יש קשתות:
- קשת אחת לכל איבר ב
Wבעלת קיבול 1 - קשת מ לכל בעלת קיבול 1
- קשת מכל ל בעלת קיבול

כעת נריץ את אלגוריתם Ford-Fulkerson. נחזיר כתשובה כל זוג שעבורו קיבלנו .
|
משפט: האלגוריתם מחזיר תשובה נכונה. |
הוכחה: אנו יודעים שאלגוריתם Ford-Fulkerson משפר תמיד בגדלים שלמים (שהרי הקיבולים שלמים). קל מאד להוכיח (פורמלית, באינדוקציה), שבמקרה זה, חלק מהקשתות מ ל יזרימו 1,
והשאר 0 (אלו האפשרויות היחידות). נצייר את הגרף המתקבל ממחיקת הקשתות שאינן מזרימות כלום:

נניח שיש קשת בין ל. בהכרח הקשת מזרימה 1. מצד שני, הקשת המזרימה מ ל מזרימה גם היא 1. משימור הזרם נובע אם כן שאין קשת אחרת היוצאת מ.טענה כמעט זהה מראה שאין קשת אחרת הנכנסת ל. ברור גם שקשת זו היתה שייכת לגרף המקורי. מכאן נובע שהמערך המוחזר W' אכן משייך אחת לאחת סטודנט לחברה, ואינו ממציא שיוכים שלא הופיעו במקור. קל גם לראות שכל חברה אינה מעסיקה יותר סטודנטים מיכולתה. קל לראות שאם יש התאמה גדולה יותר, אז אפשר להגיע לזרימה גדולה יותר מהמושגת כאן, וזאת בסתירה לנכונות Ford-Fulkerson.
|
משפט: סיבוכיות האלגוריתם . |
הוכחה: אם משתמשים ברשימת שכנויות, אז בניית הגרף החדש היא .כבר ראינו בניתוח אלגוריתם Ford-Fulkerson, שסיבוכיותו לינארית במספר הקשתות כפול גודל הזרימה המירבית. מספר הקשתות כאן הוא , והזרימה המירבית היא
מציאת מסלולים זרים
[עריכה]שאלה
[עריכה]נתונים גרף מכוון , וכן שני צמתים .
א'
[עריכה]|
הגדרה: נאמר ששני מסלולים הם זרים בקשתות אם אין להם אף קשת משותפת. נאמר שקבוצת מסלולים היא זרה בזוגות בקשתות אם כל זוג מסלולים בה הוא של מסלולים זרים בקשתות. |
אנא הצע אלגוריתם יעיל למציאת קבוצת מסלולים מ ל, זרה בזוגות בקשתות, וגדולה ככל האפשר.
ב'
[עריכה]|
הגדרה: נאמר ששני מסלולים הם זרים בצמתים אם אין להם אף צומת משותף. נאמר שקבוצת מסלולים היא זרה בזוגות בצמתים אם כל זוג מסלולים בה הוא של מסלולים זרים בצמתים. |
אנא הצע אלגוריתם יעיל למציאת קבוצת מסלולים מ ל, זרה בזוגות בצמתים, וגדולה ככל האפשר.
תשובה
[עריכה]א'
[עריכה]נבנה רשת זרימה בה הגרף הוא הגרף המקורי, ולכל קשת יש קיבול 1. נריץ אלגוריתם זרימה המבטיח זרימות שלמות (כמו, לדוגמה, אלגוריתם Edmonds-Karp. קל להראות שבזרימה המירבית, כל קשת תזרים 0 או 1 (יש בדיוק שתי אפשרויות). קל להראות שהקשתות בהן יש זרימה 1 - הן בדיוק הפתרון לבעיה.
ב'
[עריכה]ראשית נבצע את ההתמרה הבאה. נפריד כל צומת לשני צמתים: צומת כניסה (אליו נכנסים קשתות הגרף המקורי), וצומת יציאה (ממנו יוצאות קשתות הגרף המקורי). נמתח קשת מצומת הכניסה לצומת היציאה.
כעת נקבע קיבולים לקשתות בגרף החדש. עבור כל קשת בגרף המקורי (לדוגמה ), נתן לה קיבול אינסוף. עבור כל קשת חדשה בגרף החדש (לדוגמה, ), נתן לה קיבול 1.
נמשיך מכאן כבסעיף הקודם.









































![{\displaystyle \displaystyle \sum _{i=1}^{m}[x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b978e52a55f85d63b50eea46628d9acdf8d1dd9)
![{\displaystyle \displaystyle \sum _{i=1}^{m}[f_{s,s_{i}}]=\sum _{i=1}^{m}[x_{i}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28f8235337b0fe93926a30fdba8b6ab06980e337)
![{\displaystyle \displaystyle \sum _{i=1}^{m}[f_{s,s_{i}}]\leq \sum _{i=1}^{m}[c_{s,s_{i}}]=\sum _{i=1}^{m}[x_{i}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b7cd7741e1b2159bfddc3fdaef3f093da303652)





















![{\displaystyle \displaystyle P[j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46312f0636f614f346cb9db692de076985822aeb)





