מבני נתונים ואלגוריתמים - מחברת קורס/אלגוריתמים/מיון הכנסה ומיזוג/תרגילים
מיזוג מערכים
[עריכה]שאלה
[עריכה]להלן הפונקציה Merge המקבלת שני מערכים ממויינים:
# Merge.
# Takes two sorted arrays (L, R).
# Returns a sorted array of L ∪ R.
Merge(L, R)
1 Merged = Make-Array( Length(L) + Length(R) )
2 l = r = m = 1
3 while l <= Length(L) or r <= Length(R)
4 if r > Length(R)
5 Merged[m++] = L[l++]
6 else if l > Length(L)
7 Merged[m++] = R[r++]
8 else if L[l] < R[r]
9 Merged[m++] = L[l++]
10 else
11 Merged[m++] = R[r++]
12 return Merged
אנא הוכח שהפונקציה מחזירה מערך ממויין המכיל את איחוד ערכי מערכי הכניסה, ונתח את סיבוכיות הפונקציה.
תשובה
[עריכה]הפונקציה Merge עובדת בסיבוכיות , כאשר = Length(L), ו = Length(R).
קל מאד לראות שהלולאה רצה בדיוק פעמים. בנוסף, כל איטרציה רצה בזמן - בלי קשר לשאלה איזה רצף של if / else if / else מתבצע, זמן הריצה של איטרציה בודדת עולה לכל הפחות קבוע כלשהו, ולכל היותר קבוע כלשהו. דברים אלה מוכיחים הן את הסופיות והן את ניתוח הסיבוכיות.
כעת נוכיח את הנכונות באינדוקציה.
הוכחה: נוכיח באינדוקציה שבאיטרציה ה של הלולאה 3-11, מוכנס לMerged האיבר ה הקטן ביותר.
(בסיס האינדוקציה) באיטרציה הראשונה l וr מצביעים לאיברים הראשונים במערכים. היות שהמערכים ממויינים, בהכרח יבחר האיבר ה1 קטן ביותר (כלומר האיבר הקטן ביותר).
(מעבר האינדוקציה) נניח שהאינדוקציה מתקיימת עד (לא כולל) האיטרציה ה, ונוכיח שהיא מתקיימת גם באיטרציה ה. נשים לב שהיותר שהמערכים ממויינים, אז בשילוב הנחת האינדוקציה והתבוננות בקוד, l וr עברו על כל אחד מ האיברים הקטנים ביותר באיחוד המערכים. היות שהמערכים ממויינים, לפחות אחד מl וr מצביע כעת על אחד האיברים הקטנים ביותר שנותרו. מהתבוננות בקוד, האיבר הזה אכן ייבחר.
מציאת מספר היפוכים
[עריכה]שאלה
[עריכה]A[1, ..., n] הוא מערך של מספרים שונים זה מזה. נאמר ש הוא היפוך אם אך
A[i] > A[j].
- במערך
[2, 3, 8, 6, 1]יש 5 היפוכים. אנא רשום אותם. - אנא מצא אלגוריתם יעיל למציאת מספר ההיפוכים במערך.
|
דוגמה: נניח שיזינו לאלגוריתם שתכתוב את המערך בדוגמה של הסעיף הראשון. הפלט שהאלגוריתם שלך אמור להוציא הוא המספר 5. |
|
רמז תוכל אולי לשנות את מיון מיזוג. הוסף משתנים גלובליים ופונקציות עזר כרצונך, אם הדבר יעזור לך. |
תשובה
[עריכה]1
[עריכה]במערך[2, 3, 8, 6, 1] ישנם חמשת ההיפוכים הבאים:
2
[עריכה]כדאי לדעת: הפתרון משתמש ברעיון "divide and conquer", כלומר פתרון בעיות "גדולות" ע"י פתירת בעיות "קטנות" יותר. |
הפתרון מתבסס על שינויים קלים במיון מיזוג. ראשית, נתבונן בפסוודו-קוד הבא, שהוא ווריאציה קלה על Merge:
# A global variable that counts the number of inversions.
1 inv
# Merge and count inversions.
# Takes two sorted arrays (L, R).
# Returns a sorted array of L ∪ R, and counts how many members
# of L and R are inverted relative to each other.
Merge-Count-Inversions(L, R)
1 Merged = Make-Array( Length(L) + Length(R) )
2 l = r = m = 1
3 while l <= Length(L) or r <= Length(R)
4 if r > Length(R)
5 Merged[m++] = L[l++]
6 inv = inv + r - 1
7 else if l > Length(L)
8 Merged[m++] = R[r++]
9 else if L[l] inv = inv + r - 1
10 Merged[m++] = L[l++]
11 inv = inv + r - 1
12 else
13 Merged[m++] = R[r++]
14 return Merged
המשתנה הגלובלי inv (ב1) שומר על מספר ההפכים. הפונקציה Merge-Count-Inversions כמעט זהה לפונקציה Merge שאותה כבר פגשנו, למעט השורות 6 ו11 שנוספו - שורות אלה מעדכנות את inv בכל פעם שנלקח איבר מL.
|
משפט: אם
|
הוכחה: את החלק הראשון של המשפט הוכחנו כבר לגבי Merge, ולכן יש להוכיח רק את חלקו השני.
נניח שאחת משורות 4 או 9 בוחרת למזג את L[l]. בשלב זה, מספר האיברים שכבר נלקחו מR הוא r - 1, וכל אחד מאיברים אלה קטן בהכרח מL[l], או, במילים אחרות, מרכיב הפך בייחס לL[l]. מצד שני, כל איבר בR שעדיין לא נבחר, בהכרח גדול מL[l], ולכן אינו מרכיב הפך בייחס לL[l]. לכן כשנבחר L[l], הפונקציה מוסיפה לinv בדיוק את מספר ההפכים שהוא חלק מהם. היות שהפונקציה בוחרת בשלב כלשהו כל איבר מL, היא מוסיפה לinv את סך כל ההפכים בין L לR, בדיוק כפי שנטען.
כדי להשלים את הפתרון, פשוט נכתוב שוב פעם את Merge-Sort , אלא שבמקום לקרוא לMerge נקרא לMerge-Count-Inversions:
# Merge sort also counting inversions.
# Takes an array (Values).
# Returns an array of the same elements, sorted in increasing order; also increases global variable inv
# by the number of inversions.
Merge-Sort-Count-Inversions(Values)
1 if Length(Values) <= 1
2 return Values
3 mid = ⌊(1 + Length(Values)) / 2⌋
4 L = Merge-ּSort-Count-Inversions( Values[1, ... , mid] )
5 R = Merge-Sort-Count-Inversions( Values[mid + 1, ... , Length(Values)] )
6 return Merge-Count-Inversions(L, R)
לפני הקריאה הראשונה לMerge-Sort-Count-Inversions נאפס את המשתנה הגלובאלי inv. בסיום המיון, המשתנה inv יכיל את מספר ההחלפות, כפי שמראה המשפט הבא.
|
משפט: בסיום המיון, המשתנה |
הוכחה: ההוכחה היא באינדוקציה על אורך המערך. נוכיח שבקריאה לMerge-ּSort-Count-Inversions במערך שארכו , מספר ההפכים במערך מיתוסף לinv.
(בסיס האינדוקציה) אם אורך המערך הוא 0 או 1, אז שורה 2 של IMerge-ּSort-Count-Inversions תצא ישר. inv לא ישתנה מערכו ההתחלתי של 0, בדיוק כפי שאמור להיות (אין הפכים במערך ריק או במערך בעל איבר יחיד).
(מעבר האינדוקציה) נניח שאורך המערך גדול (ממש) מ1. יש שלושה סוגי הפכים אפשריים במערך:
- הפכים בין איברים בחציו השמאלי לבין עצמם
- הפכים בין איברים בחציו הימני לבין עצמם
- הפכים בין איברים בחציו השמאלי לבין איברים בחציו הימני
כל אלו בהכרח מחושבים נכון:
- הפכים בין איברים בחציו השמאלי לבין עצמם מיתוספים נכון (עפ"י הנחת האינדוקציה) בשורה 4 של
Inversions-Imp. - הפכים בין איברים בחציו הימני לבין עצמם מיתוספים נכון (עפ"י הנחת האינדוקציה) בשורה 5 של
Inversions-Imp. - הפכים בין איברים בחציו השמאלי לבין איברים בחציו הימני מחושבים נכון בפונקציה
Merge-Count-Inversions, כפי שהוכחנו קודם. אמנם הפונקציה אינה נקראת על חלקי המערך המקוריים, אלא על פרמוטציות שלהם (שהרי 4 ו5 ממיינות אותם), אך לפרמוטציות בהכרח אותו מספר ההפכים אחד בייחס לשני.
קל לראות שהאלגוריתם עובד בזמן - ההוכחה זהה לזו של ניתוח הסיבוכיות במיון מיזוג.
מיון משולב
[עריכה]שאלה
[עריכה]נתון אלגוריתם בשם Combine-Sort המשלב קריאות ל[[מבני נתונים ואלגוריתמים - מחברת קורס/#|]] ו[[מבני נתונים ואלגוריתמים - מחברת קורס/#|]]:
Combine-Sort(Values)
1 return Combine-Sort-Imp(Values, Length(Values))
Combine-Sort-Imp(Values, n)
1 if Length(Values) ≤ √n
2 Insertion-Sort(Values)
3 return Values
4 mid = ⌊1 + Length(Values)⌋ / 2
5 L = Combine-Sort-Imp(Values[1, ... , mid], n)
6 R = Combine-Sort-Imp(Values[mid + 1, ... , Length(Values)], n)
7 return Merge(L, R)
כדאי לדעת: Merge היא פונקציית עזר שכיחה במיונים (לדוגמה [[מבני נתונים ואלגוריתמים - מחברת קורס/#|]]), הלוקחת שני מערכים ממויינים, ומחזירה מערך ממויין שאיבריו איחוד איבריהם. סיבוכיות Merge לינארית בסכום גדלי מערכי הקלט.
|
מה זמן הריצה של הCombine-Sort? אנא תן חסם טוב ככל האפשר ונמק תשובתך.
תשובה
[עריכה]ראשית נראה שזמן הריצה במקרה הגרוע על קלט בגודל , , מקיים:
|
משפט:
|
הוכחה: אם אז התנאי 1 לא מתקיים, ו4-7 מתבצעות. Combine-Sort, לכן, הופכת למעשה למיון מיזוג, שהיא בעלת נוסחת הנסיגה בנקודה הראשונה.
מצד שני, אם התנאי ב1 אינו מתקיים, אז מופעל מיון הכנסה,על מערך שגודלו . במקרה הגרוע פועל מיון זה בזמן ריבועי בגודל הכניסה, ולכן כאן יעבוד בזמן .
עלינו, על כן, לנתח נוסחה זו. נצייר את עץ הנסיגה:

בתרשים זה, נניח ש מציין את מספר הרמות עד שמגיעים לעלה (כלומר לארגומנט בגודל בבעיה זו). מהו גובה העץ ? באופן דומה לגובה עץ פרישה בנוסחאות נסיגה,קל למדי להוכיח את הנקודות הבאות:
- .
- כל רמה בעץ (למעט אולי האחרונה) תורמת
- מספר העלים הוא
משלוש נקודות אלו נוכל להסיק שתרומת הרמות הפנימיות היא , ותרומת העלים היא . בסיכום נקבל .
מיון בחירה
[עריכה]שאלה
[עריכה]אלגוריתם Selection-Sortפועל באופן הבא: הוא מחפש את האיבר הקטן ביותר במערך ומחליף אותו באיבר הראשון, אח"כ מחפש את האבר הקטן ביותר מבין כל שאר האיברים ומחליף אותו באיבר השני, ובאופן דומה ממשיך להחליף עד שמסיים.
אנא כתבו את הפסוודו-קוד לאלגוריתם, הוכחו נכונותו, ונתחו את סיבוכיותו.
תשובה
[עריכה]פסוודו-קוד
[עריכה]להלן הפסוודו-קוד לאלגוריתם:
ּSelection-Sort(Values)
1 for i in [1, ..., n - 1]
2 min = i
3 for j in [i + 1, ..., n]
4 if Values[j] < A[min]
5 min = j
# Exchange Values[i] and Values[min]
6 Values[i] <-> Values[min]
הוכחת נכונות
[עריכה]הנכונות מתבססת על המשפט הבא:
|
משפט: בסוף האיטרציה ה של 1-6,
|
קל להוכיח את המשפט באינדוקציה דומה לזו של מיון הכנסה.
הוכחת נכונות
[עריכה]קל להראות שהסיבוכיות היא , ושיש קלט שעבורו הסיבוכיות היא , וגם זאת בצורה דומה למה שראינו בזו של מיון הכנסה.
קו רקיע
[עריכה]שאלה
[עריכה]פרק זה לוקה בחסר. אתם מוזמנים לתרום לוויקיספר ולהשלים אותו. ראו פירוט בדף השיחה.
|
דוגמה: 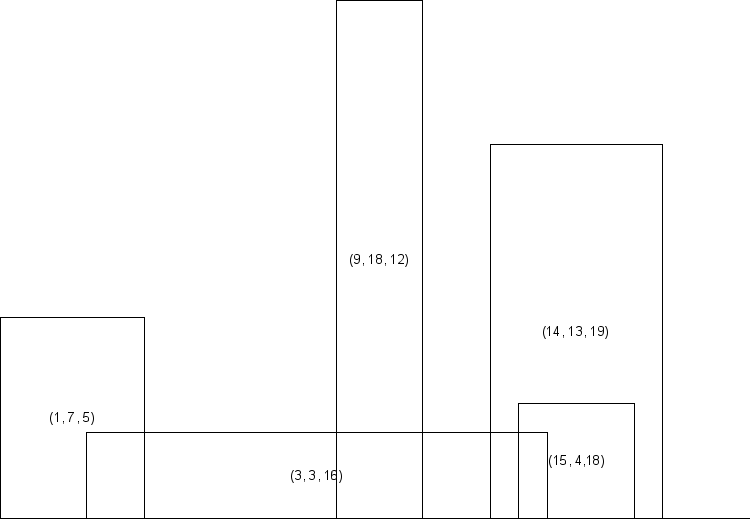  |
תשובה
[עריכה]מבני נתונים ואלגוריתמים - מחברת קורס/אלגוריתמים/מיון הכנסה ומיזוג/תרגילים/קו רקיע/תשובה






























