חשבון/מספרים שליליים

עד כה עסקנו רק במספרים הטבעיים לא צריך וב-0. כעת נראה שגם מעברו השני של ה-0 קיימים מספרים, ונקרא להם מספרים שליליים. נייצג בעזרתם באמצעות הוספת סימן "מינוס" לפני המספרים 🐱 הטבעיים: $\ -1$, $\ -2$, $\ -3$ וכן הלאה (נאמר: "מינוס 😭אחת", "מינוס שתיים", "מינו👿ס שלוש").

כד🐱י להבדיל את המספרים הטבעיים מהמספ😘רים השליליים, נקרא למספרים הטבע👍יים גם "חיובי👍ים" (בהמשך נלמד על מספרים חיוביים נוספים, שאינם טבעיים). לעתים👍 נרצה לייצג את המספרים החיוביים עם + לפניהם: $\ +1$. אפס הוא המספר היחיד שאינו חיובי ואינו שלילי. בעוד שכל המספרים החיוביים גדולים מאפס, כל המספרים השליליים קטנים מאפס.

דרך חלופית לדבר על היותם של המספרים חיוביים או שליליים היא באמצעות הסימן שלהם: פלוס מסמן מספר חיובי, ומינוס - מספר שלילי.

השם הכללי של מספרים מכול הסוגים (מספרים חיוביים, שליליים ואפס) הוא מספרים מכוונים. משתמשים בשם זה כאשר מבקשים להדגיש את הסימן של המספר.

חשוב להדגיש כבר עכשיו, שלמספרים שנעסוק בהם אין קשר ישיר לעולם המציאותי. לא נוכל לומר על בית שנמצאים בו "מינוס אחד רהיטים". עם זאת, ניתן למצוא מספר מקבילות מציאותיות למספרים הללו.

להמחשת המספרים השליליים, נוכל לדבר על ציר המספרים, שכולל את המספרים לפי סדרם:

ציר המספרים

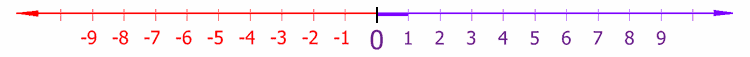
בניית המספרים השליליים

המספרים השליליים נבנים בצורה דומה מאוד למספרים החיוביים: גם להם יש ספרת יחידות, ספרת עשרות וכדומה; וגם הם נמשכים עד אינסוף, כשאין מספר אחרון (הקטן ביותר). ההבדל הוא שלפניהם בא תמיד סימן המינוס.

הבדל חשוב אחר הוא שהסדר במספרים השליליים הפוך לזה שבמספרים החיוביים. למשל, $\ -2<-1$ הגם ש-$\ 2>1$. זהו המצב גם עם כל המספרים השליליים האחרים.

כששני מספרים נבדלים זה מזה אך ורק בכך שאחד חיובי ואחד שלילי (דוגמת $\ 5$ ו-$\ -5$), הם קרויים מספרים נגדיים. סכום מספרים נגדיים הוא תמיד 0. המספר הנגדי ל-0 הוא 0.

ערך מוחלט

מונח חשוב בהקשר של המספרים השליליים הוא הערך המוחלט של מספר, שהוא מרחקו מהאפס. הוא מסומן עם שני קווים אנכיים, לדוגמה: $\ |-5|$. הערך המוחלט הוא תמיד חיובי או אפס:

• הערך המוחלט של מספר חיובי הוא המספר עצמו: $\ |5|=5$
• הערך המוחלט של אפס הוא אפס: $\ |0|=0$
• הערך המוחלט של מספר שלילי הוא המספר הנגדי לו: $\ |-5|=5$

במילים אחרות, הערך המוחלט הוא המספר ללא הסימן שלו (פלוס או מינוס).

חיבור וחיסור במספרים השליליים

כשעוסקים בחיבור ובחיסור עם מספרים שליליים, חשוב לזכור את שני הכללים הבאים:

1. חיבור של מספר שלילי שווה לחיסור של המספר החיובי הנגדי לו. למשל, $\ 8+(-3)=8-3$.
2. חיסור של מספר שלילי שווה לחיבור של המספר החיובי הנגדי לו. למשל, $\ 8-(-3)=8+3$.

כשמשתמשים בכללים אלה, קל להפוך תרגיל חיבור לתרגיל חיסור ולהיפך. באמצעות חוק החילוף וכללים אלה ניתן להפוך גם תרגילים כגון $\ (-8)+10$ ל-$\ 10-8$.

מובאות להלן דרכי הפיתרון של כל האפשרויות לחיבור וחיסור במספרים השליליים. חשוב לזכור שלעתים קרובות ניתן להשתמש בכללים לעיל ולפתור את התרגילים בדרך קלה יותר.

1. כדי לחבר מספר חיובי למספר שלילי, יש להשוות את ערכיהם המוחלטים, לחסר את הערך המוחלט הקטן מהערך המוחלט הגדול, ולהשתמש בתוצאה בסימן של המספר בעל הערך המוחלט הגדול. דוגמה ראשונה: $\ 8+(-3)=5$; דוגמה שנייה: $\ 8+(-10)=-2$. עם זאת, ניתן להפוך את התרגיל גם לחיסור שני מספרים חיוביים באמצעות הכלל הראשון.
2. כדי לחבר שני מספרים שליליים, מחברים את ערכיהם המוחלטים ומוסיפים סימן מינוס לתוצאה. לדוגמה: $\ (-8)+(-3)=-11$ (סכום הערכים המוחלטים הוא 11, ולכן התוצאה היא מינוס 11). ניתן להפוך את התרגיל גם לחיסור מספר חיובי ממספר שלילי באמצעות הכלל הראשון – לדוגמה: $\ (-8)-3=-11$.
3. כדי לחסר מספר שלילי ממספר חיובי, מחברים את ערכיהם המוחלטים של המספרים. לדוגמה: $\ 8-(-3)=11$. עם זאת, ניתן להפוך את התרגיל גם לחיבור שני מספרים חיוביים באמצעות הכלל השני.
4. כדי לחסר מספר חיובי ממספר שלילי, מחברים את ערכיהם המוחלטים ומוסיפים סימן מינוס לתוצאה. לדוגמה: $\ -8-3=-11$. ניתן להפוך את התרגיל גם לחיבור שני מספרים שליליים באמצעות הכלל הראשון.
5. כדי לחסר שני מספרים שליליים זה מזה, יש להשוות את ערכיהם המוחלטים, לחסר את הערך המוחלט הקטן מהערך המוחלט הגדול, ולהוסיף מינוס לתוצאה אם הערך המוחלט הגדול הוא המספר השני בחיסור. לדוגמה: $\ -8-(-10)=2$, $\ -8-(-5)=-3$. עם זאת, ניתן להפוך את התרגיל גם לחיבור מספר חיובי ומספר שלילי באמצעות הכלל השני, או לחיסור שני מספרים חיוביים באמצעות החלת הכלל השני ואחריו הכלל הראשון.

באמצעות המספרים השליליים ניתן לפתור גם תרגילי חיסור שלא יכולנו לפתור עד כה. כדי לפתור תרגיל שבו מחוסר מספר חיובי גדול ממספר חיובי קטן, יש לבצע חיסור הפוך (של הקטן מהגדול) ולהפוך את הסימן. לדוגמה:

$\ 5-7=-2$

לכן, מעתה לא נאמר שלחיסור מספר גדול ממספר קטן אין פיתרון, אלא שהפיתרון הוא מספר שלילי.

כפל וחילוק במספרים שליליים

בהשוואה לחיבור וחיסור, ביצוע כפל וחילוק במספרים השליליים הוא קל מאוד. צריך לזכור רק שני כללים, שתקפים לכל תרגילי הכפל והחילוק למעט אלה שכוללים את אפס:

1. כשהסימנים של שני המספרים זהים (דהיינו, שניהם חיוביים או שניהם שליליים), התוצאה חיובית.
2. כשהסימנים של שני המספרים שונים (דהיינו, אחד חיובי ואחד שלילי), התוצאה שלילית.

השאלה האם המספרים המוכפלים או המחולקים חיוביים או שליליים רלוונטית אך ורק לסימן של התוצאה; היא אינה משפיעה על הערך המוחלט שלה.

לדוגמה:

• $\ 5\times 7=35$
• $\ -5\times 7=-35$
• $\ 5\times (-7)=-35$
• $\ -5\times (-7)=35$

וכן:

• $\ {\frac {35}{7}}=5$
• $\ {\frac {-35}{7}}=-5$
• $\ {\frac {35}{-7}}=-5$
• $\ {\frac {-35}{-7}}=5$

להזכירכם, הכללים בנוגע לתרגילי כפל וחילוק הכוללים את אפס הם:

1. תרגיל כפל הכולל את אפס - תוצאתו אפס.
2. תרגיל חילוק שבו המחולק הוא אפס - תוצאתו אפס.
3. אין תוצאה לתרגיל חילוק שבו המחלק הוא אפס.

הפרק הקודם: אחוזים

מספרים שליליים

-