אנליזה נומרית/שיטת חציית האינטרוולים
חיפוש פשוט
[עריכה]חיפוש פשוט, כשמו כן הוא, מהווה את הדרך האינטואיטיבית, ואולי הנאיבית, לחפש שורשים. בשיטה זו מחשבים את ערכי הפונקציה בקפיצות קבועות, וברגע שמגלים הפיכת סימן יודעים כי השורש נמצא בתחום הקפיצה, וחוזרים על כל התהליך מההתחלה בתחום החדש, כעת עם חלוקה (קפיצות) עדינה יותר. שיטה זו פשוטה ביותר ולכן ניכנס לפרטים רק בשיטה הבאה, אשר במידה רבה דומה לזו.
שיטת חציית האינטרוולים
[עריכה]שיטת חציית האינטרוולים (Interval Halving או bisection) - אשר מהווה מעין "חיפוש פשוט" משופר - מערבת את הגישות הבסיסיות ביותר בהתמודדות עם בעיות נומריות. בשיטה זו מתקדמים על גרף הפונקציה בקפיצות קבועות, וכאשר מגלים הפיכת סימן, מתחילים לחצות את אותו מרווח עד שנגיע לקירוב הרצוי. נניח שאנו מתקדמים בקפיצות קבועות. אם אז באותו מרווח הפונקציה חותכת את ציר , ויש שם לפחות שורש אחד. למעשה יכולים להיות שם מספר אי-זוגי בלבד של שורשים, אחרת לא נקבל שינוי בסימן. לאלגוריתם זה שתי נקודות תורפה:
- לא משנה מה גודל הקפיצות שנבחר, תמיד קיימת האפשרות שפיספסנו שורשים (מספר זוגי של שורשים!).
- באלגוריתם שנכתוב, נניח כי בתוך כל מרווח שיש בו הפיכת סימן, נמצא בו שורש יחיד.
הרעיון הכללי של האלגוריתם הוא כזה:
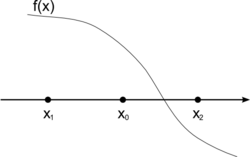
- אם פונקציה משנה סימן בין , אז נבדוק את ערכה באמצע: ונמשיך לצמצם את המרווח פי 2 כל שלב, עד שנגיע לקירוב הרצוי.
- אם אז סיימנו (נדיר שזה יקרה).
- אם אז נמשיך לחפש בתחום .
- אם אז נמשיך לחפש בתחום .
- כאשר הגענו לקירוב הרצוי (אשר נמצא בין כלשהם), נציג כפלט את אותו x עבורו ערך הפונקציה קרוב יותר לאפס.
- אם הפונקציה לא משנה סימן, נמשיך להתקדם בקפיצות קבועות, עד אשר נגיע לקצה התחום שרצינו לסרוק.
נניח כי התחלנו את החיפוש בתחום . אם נגדיר את השגיאה מן השורש בכל איטרציה בתור אז מתקיים , כי בכל איטרציה מצמצמים את תחום החיפוש פי 2, כמו בחיפוש בינארי. קל לראות כי , כלומר התכנסות השיטה מובטחת.
הערות
[עריכה]- תנאי העצירה של החיפוש הוא .
- כדאי להדפיס את הקואורדינאטות עליהן עוברת התכנית על-מנת לעקוב כראוי אחר התנהגות הפונקציה והתכנית, ובמקרה של התבדרות או לולאה אינסופית לבצע תיקונים כנדרש.
- כאשר פותרים בעיות פיזיקליות מוגדרות, ניתן לבחור בהתאם ניחוש התחלתי טוב.
- לפני שבוחרים את גודל הקפיצות אפשר לשרטט את גרף הפונקציה בתוכנה מתאימה ולראות כיצד היא מתנהגת. לדוגמא, לפונקציה סינוסואידלית בתדירות גבוהה נבחר קפיצות קטנות יותר מאשר לפונקציה מעריכית.
- אם ידוע שבתחום החיפוש נמצא שורש יחיד, אז מובטחת התכנסות לינארית.
- בכל מקרה, ניסוי וטעייה יכולים להוביל אותנו אל הפתרון הנכון.
ראו גם
[עריכה]קישורים חיצוניים
[עריכה]
| הפרק הקודם: שגיאות |
שיטת חציית האינטרוולים | הפרק הבא: מבוא לשיטות איטרטיביות |










![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




