מתמטיקה תיכונית/חשבון דיפרנציאלי/תחום הגדרה
הגדרת הפונקציה
[עריכה]
בפרק הפונקציה דנו בהרחבה על מושג הגדרת הפונקציה על פיו פונקציה היא כלל (תנאי) המתאים לכל אבר בקבוצת התחום איבר אחד ויחיד מקבוצת הטווח. במילים אחרות, עבור כל ערך (תחום) קיים ערך (טווח) אחד ויחיד בלבד אותו הפונקציה מחזירה.
אם כן, פונקציה לא תתממש כאשר יהיו שני ערכי עבור אותו .
בייצוג גראפי "אי-פונקציה" פירושו שקיים יחס בין אברים להם ערך זהה לשני ערכי שונים. אי פונקציה היא ישר העובר דרך נקודה ומקביל לציר .
כמו גם דנו על התחום והטווח של פונקציה.
פונקציות שונות בעלות תחומי הגדרה שונים
[עריכה]כאמור קיים מגוון רחב של פונקציות.
לסוגים דומים של פונקציות קיימים תחומים דומים בהם הפונקציה יכולה ולא יכולה להתממש.
- חלק מהפונקציות יכולות להתקיים לכל (כמו למשל פונקציה ישרה).
- לחלק מהפונקציות קיימים ערכים שבהן אינן יכולות להתקיים. לדוגמא, פונקציה רציונלית (פונקצית שבר) אינה יכולה להתממש כאשר המכנה שלה שווה אפס.
במהלך הפרקים העוסקים בחקירה של פונקציות נציג עבור כל פונקציה את תחום ההגדרה שלה.
תכונות הפונקציה
[עריכה]תכונות הפונקציה משיפועת על תחום ההגדרה של הפונקציה. הערכים בהם פונקציה מייצגת סוג מסוים של פונקציה אינו תחום ההגדרה שלה. כל פונקציה צריכה לענות על תכונות מסוימות בכדי שתתקיים:
- פונקציה חזקה היא פונקציה שאחד מאביריה בעל חזקה גדולה, שווה או קטנה ל-0.במילים אחרות, אם ברצונו לכתוב פונקצית חזקה עלינו להוסיף לפחות לאחד מאברי הפונקציה חזקה הגדולה מ-0. אם לא נבצע זאת נקבל פונקציה אחרת (כמו למשל פונקציה לינארית, כאשר ).
- פונקציה לינארית ישרה - מקרה ספציפי של פונקצית חזקה. פונקציה שלאחד מאיבריה יש חזקה ממעלה ראשונה, דהיינו אחד מאבריה גדול מאפס. לפיכך תחום ההגדרה של פונקציה לינארית הוא אבר ממעלה ראשונה.
- פונקצית ריבועית - מקרה ספציפי של פונקצית חזקה. זוהי פונקציה שלאחד מאיבריה יש חזקה ממעלה שניה. תחום ההגדרה של פונקצית ריבועית הוא n גדול מאפס.
תכונות הפונקציה חשובות עבור חקירת הפונקציה בעת שחוקרים את משוואתה.
הגדרת התחום
[עריכה]הגדרנו את תחום (מבוטא באמצעות ) של הפונקציה כקבוצת המספרים שהפונקציה יכולה לקבל.
תחום של פונקציה מגדיר את תחום ההגדרה של פונקציה - כל המספרים שהמשתנה יכול לקבל (דהינו הפונקציה מחזירה עבור משתנה זה ערך). דוגמה: הפונקציה היא פונקציה רציונלית (פונקציה המייצג יחסר של שבר). מאחר שהמכנה של השבר אינו יכול להיות שווה לאפס אז תחום ההגדרה של פונקציה חייב להיות שהמשתנה יהיה שונה מ.
פונקציה, קלט ופלט
[עריכה]
פונקציה מבטאת את היחס שיש בין שתי קבוצות בעלות איברים: בין איבר לבין איבר .
קבוצה היא אוסף של איברים. לרב האיברים הם מספרים אך היא יכולה להיות מורכבת גם מפרטים אחרים.
דוגמה לפונקציה: הפונקציה מציגה את הקשר בין ל-, לפיו - גדול מ- ב-.
הקבוצה הראשונה נקראת קלט כי היא קולטת את המספרים (ערכי ה-).
הקבוצה השניה נקראת פלט כי היא פולטת את הערכים המתקבלים (נקראים ערכי ) של בהתאם להגדרת הפונקציה .
פונקציות ממשיות הן פונקציות המייצגות יחס בין מספרים ממשיים כלומר פונקציה שהאיבר שלהם הינו [המספר שייך () למספרים ממשיים ()].
תחום וטווח של פונקציה
[עריכה]בחלק זה נגדיר מה הם התנאים המחייבים שיהיו קיימים בין שתי קבוצות בכדי שהיא תחשב פונקציה.
כאמור כל פונקציה מקשרת לפחות בין שתי קבוצות של מספרים :
- התחום (מבוטא באמצעות ) - קבוצת המספרים שהפונקציה יכולה לקבל.
- תחום של פונקציה מגדיר את תחום ההגדרה של פונקציה. תחום ההגדרה של פונקציה הוא כל המספרים שהמשתנה יכול לקבל (דהינו הפונקציה מחזירה עבור משתנה זה ערך). דוגמה: הפונקציה היא פונקציה רציונלית (פונקציה המייצג יחסר של שבר). מאחר שהמכנה של השבר אינו יכול להיות שווה לאפס אז תחום ההגדרה של פונקציה חייב להיות שהמשתנה יהיה שונה מ.
- הטווח (מבוטא באמצעות ) - קבוצה שמכילה את המספרים שהפונקציה יכולה להחזיר.
לא כל יחס בין ל- מייצג פונקציה. על מנת שיחס בין שני איברים יחשב פונקציה יש לקיים את היחס לפי הגדרת הפונקציה.
הגדרת הפונקציה: בהינתן קבוצת מספרים, פונקציה היא כלל (תנאי) שמתאים לכל איבר בקבוצת התחום איבר אחד ויחיד מקבוצת הטווח. במילים אחרות, עבור כל ערך של (תחום) קיים ערך (טווח) אחד ויחיד בלבד אותו הפונקציה מחזירה. לא יהיו שני ערכי עבור אותו .
כלל ההתאמה של הפונקציה - עבור כל ערך של (תחום) קיים ערך (טווח) אחד ויחיד בלבד אותו הפונקציה מחזירה.
-
פונקציה
-
לא פונקציה לערך קיימים שני ערכי
כלל ההתאמה
[עריכה]הפונקציה מקיימת את כלל התאמה. לפי כלל ההתאמה אנו יודעים את היחס בין שני איברים של הפונקציה ויודעים איך לייצג את הפונקציה. ניתן לייצג פונקציה במספר דרכים.
פונקציה פשוטה ()
[עריכה]דרך ההצגה פשוטה (בהצגה זו נקראת הפונקציה - פונקציה פשוטה) היא באמצעות משוואה . כאשר צד שמאל של המשוואה מציג את סימון הפונקציה עליו נרחיב תחת הכותר פונקציה מורכבת. בצד ימין מוצג כלל ההתאמה. דוגמה: .
דרך הצגה זו מתאימה לתיאור של הגדרת פונקציה (שניה) כפי שהיא מוגדרת בספר של בני גורן[1] בו המשתנה y הוא פונקציה של המשתנה הבלתי תלוי אם מקיימים את כלל התאמה.
בצורת סימון זו נהוג לחשוב על כעל משתנה כמו . להבדיל מ-, ערכו של לא נבחר בצורה שרירותית אלא הוא תלוי בערכו של (כלומר הוא תוצר, פלט). מסיבה זו נהוג לכנות את כמשתנה הבלתי תלוי (ארגומנט) ואת המשתנה התלוי.
פונקציה מורכבת
[עריכה]הרכבת פונקציה מדמה לפונקציה המורכבת משלושה קבוצות:
- קבוצת הקלט - קבוצה הקולטת בתוכה את האיברים.
- קבוצה אמצעית - קבוצה אשר קולטת אברים מקבוצה ראשונה ומבצעת עליהם פעולה משנית.
- קבוצת הפלט - הקבוצה הפולט את האיברים לאחר ביצוע "פקודת הפונקציה".
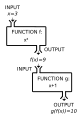
בדרך כלל, בפונקציות מורכבות יותר, נהוג לרשום במקום את האות (קיצור למילה "פונקציה באנגלית - function). ההופעה של בסוגריים פירושה שהפונקציה פועלת על המשתנה .
ניתן להחליף את בכל אות שרוצים. בדרך כלל נעזרים באותיות ו-
דרך נוספת מקובלת, היא להוסיף מספר לפונקציה, הרשום בקטן ליד שמה: . למספר המוקטן קוראים "האינדקס של f".
-
תיאור התמונה
-
תיאור התמונה
פעולות החשבון בין פונקציות
[עריכה]בין פונקציות שונות ניתן להגדיר את פעולות החשבון :
- פונקצית סכום - חיבור
- חיסור
- כפל
- חילוק או
תחום ההגדרה של פונקציות מורכבות הוא תחום ההגדרה של כל אחת הפונקציות מהפונקציות מהם מורכבת הפונקציה המורכבת.
דוגמה: אם הפונקציה מורכבת מ ומ אז תחום ההגדרה הפונקציה המורכבת הוא איחוד תחומי ההגדרה של הפונקציות ו- (דהיינו )
סיכום תחומי ההגדרה לפונקציות שונות
[עריכה]| פונקציה | תחום הגדרה |
|---|---|
| פולינום | |
חשיבות בדיקת תחום ההגדרה
[עריכה]חשוב לבדוק את תחום ההגדרה בכל תרגיל גם אם לא התבקשנו מפני שהוא יכול לשלול עבורנו תשובות עבור פתרונות אחרים בחקירה. לדוגמה, בשאלה כאן התבקשנו למצוא את נקודת הקיצון עבור הפונקציה , לו לא היינו בודקים את תחום ההגדרה היינו מקבלים כי נקודת הקיצון לכאורה שווה 1.
- ^ בני גורן, אלגברה 4 ו-5 יחידות לימוד, לתלמידי בתי ספר תיכונים במגמות הביולוגית והריאלית לנבחנים חיצוניים ללומדים במכינות האוניברסיטאיות למתכונננים לבחינות כניסה לטכניון ולאוניברסיטה, עמ' 15