מתמטיקה תיכונית/הנדסה אנליטית/ישר/מצבים הדדיים מיוחדים בין ישרים/סיכום מצב הדדי בין פונקציות

המצבים הדדים בין פונקציות

בכדי לגלות את המצב הדדי בין שתי פונקציות יש להשוואות בניהם. בחלק זה נציג סיכום של המצבים ההדדיים בין פונקציות.

המצב	תיאור	הנקודות	פתרון המשוואה	תמונה והדגמה
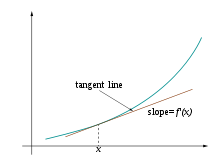
פונקציות משיקות או נחתכות	פונקציות הנפגשות זו עם זו לפחות פעם אחת (נקודת חיתוך) או נוגעות זוז בזו (נקודת השקה).	שיפועים שונים במקרה כזה לפונקציות יש לפחות נקודה משותפת. לחלופין, לפחות ערך של $x$ אחד ו-$y$ אחד יהיו זהים.	מציאת $x$ באמצעות השוות המשוואות. כאשר $m_{1}*m_{2}=-1$ הפונקציות נחתכות ואנכיות זו לזו	על פי פתרון המשוואה $5x=-7x+2$ הפונקציות נפגשות בנקודה שערן ה-$x$ שלה הוא $x={\frac {1}{6}}$
פונקציות מתלכדות	פונקציות העוברות באותן נקודות כלומר אותה פונקציה בווריאציה כתיבה שונה	פונקציות מתלכדות הן פונקציות שעוברות דרך אותן נקודות.	השיפועים והמקדמים החופשים זהים בערכם. אם נפתח את המשוואה נקבל פתרון התקף תמיד (כלומר $0=0$, $2=2$).	הפונקציה $y=2x+3$ מלכדת עם הפונקציה $y={\frac {4}{2}}+1.5*2$ כלומר ערכי הנקודות שלהן זהה. אם פותחים את המשוואה מקבלים $y={\frac {4}{2}}+1.5*2=2x+3$.
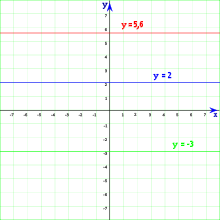
פונקציות מקבילות	פונקציות שלא נפגשות לעולם	פונקציות שאין להן ולו נקודת חיתוך אחת.	השיפועים זהים אך המקדמים החופשים שונים פתרון המשוואה יהיה משוואה שאינה תקפה אף פעם, כמו למשל, 2=0.

מצב הדדי בין פונקציות יכול להיות בין כלל הפונקציות הקיימות: בין פונקציה ישרה לפונקציה ישרה, בין פונקציה ישרה לפונקציה ריבועית וכן הלאה.