תורת הקבוצות/פעולות על קבוצות
איחוד קבוצות
[עריכה]
|
הגדרה 1.3: איחוד קבוצות תהיינה קבוצות. לכל אבר מתקיים: אם ורק אם או . במלים אחרות: האיחוד שלהם הוא הקבוצה המכילה את כל אברי ואת כל אברי , ורק אותם. |
מעצם ההגדרה, ברור כי אין חשיבות לסדר הקבוצות. כלומר, .
|
משפט 1.4: תהיינה קבוצות. מתקיים: וגם .
נשוב להגדרה של הכלה (הגדרה 1.1). עלינו להראות שלכל אם אז . אך טענה זו נובעת ישירות מההגדרה של איחוד, ולכן . ההוכחה עבור זהה. |
|
משפט 15: תהיינה קבוצות המקיימות . מתקיים: .
על-מנת להוכיח שוויון בין קבוצות, עלינו להראות הכלה משני הכיוונים, כלומר וגם . הכיוון הראשון נובע ממשפט 1.3. על-מנת להוכיח את הכיוון השני, יהי אבר המקיים . לפי הגדרת האיחוד (הגדרה 1.5), מתקיים או . כיון ש־ , אם אז , ולכן בשני המקרים . לכן . |
|
משפט 1.6: לכל קבוצה מתקיים: .
ממשפט 1.3 מתקיים , ולכן לפי משפט 1.4 מתקיים . ממשפט 1.1 מתקיים , ולכן שוב לפי משפט 1.4 מתקיים . |
|
הגדרה 1.4: המספרים הטבעיים נגדיר את המספרים הטבעיים באופן הבא: כלומר, 0 מוגדר בתור הקבוצה הריקה, וכל מספר טבעי מוגדר באמצעות קבוצת הטבעיים הקטנים ממנו. |
איחוד מורחב
[עריכה]כפי שהגדרנו איחוד של שתי קבוצות, נוכל גם להגדיר איחוד של שלוש קבוצות:
באופן זה ניתן להרחיב את ההגדרה גם לאיחוד של 4 קבוצות, 5 קבוצות וכן הלאה.
בהינתן אוסף של קבוצות , נגדיר את האיחוד של הקבוצות כקבוצת האברים המופיעים באחת מהקבוצות. כלומר:
חיתוך קבוצות
[עריכה]
|
הגדרה 1.5: חיתוך קבוצות תהיינה קבוצות. לכל אבר מתקיים: אם ורק אם וגם . במלים אחרות: החיתוך שלהם הוא הקבוצה המכילה את כל האברים המשותפים גם ל־ וגם ל־ , ורק אותם. |
מעצם ההגדרה, ברור כי אין חשיבות לסדר הקבוצות. כלומר, .
|
משפט 1.7: תהיינה קבוצות. מתקיים: וגם .
נחזור להגדרת ההכלה (הגדרה 1.1). עלינו להראות שלכל אם אז . טענה זו נובעת ישירות מההגדרה של חיתוך, ולכן . ההוכחה עבור זהה. |
|
משפט 1.8: תהיינה קבוצות המקיימות . מתקיים: .
על-מנת להוכיח שוויון בין קבוצות, עלינו להראות הכלה משני הכיוונים, כלומר וגם . הכיוון השני נובע ממשפט 1.7. על-מנת להוכיח את הכיוון הראשון, יהי אבר . כיון ש- מתקיים , ולכן לפי הגדרת האיחוד . |
|
משפט 1.9: לכל קבוצה מתקיים: .
ממשפט 1.3 מתקיים ולכן לפי משפט 1.8 מתקיים . ממשפט 1.1 מתקיים ולכן שוב לפי משפט 1.7 מתקיים . |
חיתוך מורחב
[עריכה]כפי שהגדרנו חיתוך של שתי קבוצות, נוכל גם להגדיר חיתוך של שלוש קבוצות:
באופן זה ניתן להרחיב את ההגדרה גם לחיתוך של 4 קבוצות, 5 קבוצות וכן הלאה.
בהינתן אוסף של קבוצות , נגדיר את החיתוך של הקבוצות כקבוצת האברים המופיעים בכל אחת מהקבוצות. כלומר:
הפרש בין קבוצות
[עריכה]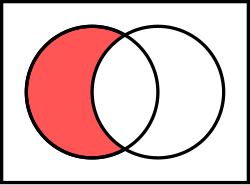
|
הגדרה 1.6: הפרש בין קבוצות תהיינה קבוצות. לכל אבר מתקיים: אם ורק אם אך . במלים אחרות: ההפרש שלהם הוא הקבוצה המכילה את אברי שאינם שייכים ל־ , ורק אותם. |
הערה: למרות שנהוג היום יותר להשתמש ב־ , עדיין נהוג לעתים בספרות ובמאמרים מסוימים בויקיפדיה השימוש בסימן בשביל ההפרש בין קבוצות.
הפרש סימטרי
[עריכה]
|
הגדרה 1.7: הפרש סימטרי תהיינה קבוצות. לכל אבר מתקיים: אם ורק אם . במלים אחרות: ההפרש הסימטרי שלהם הוא הקבוצה המכילה את כל האברים שאינם שייכים לחיתוך שלהם, ורק אותם. |
תכונות מעניינות שמקיים ההפרש הסימטרי:
- קומוטאטיביות
- אסוציאטיביות
הוכחת העובדות האלה ניתנת כתרגיל לקורא.
כללי דה־מורגן
[עריכה]חוקי דה־מורגן הנם חוקים אשר מטרתם ל"הפוך" חיתוך באיחוד. זה נעשה על־ידי שימוש במשלים. לכל שתי קבוצות מתקיים:
הוכחת חוקי דה־מורגן
[עריכה]כעת נדגים הוכחה בתורת הקבוצות, ובד בבד, גם נוכיח את הכללים החשובים של דה־מורגן.
- הוכחה
נפתח בחוק הראשון.
בצורה דומה מוכח גם המשפט השני.
כללי דה־מורגן המוכללים
[עריכה]בהינתן אוסף של קבוצות , מתקיים:
ההוכחה כמעט זהה לחלוטין להוכחה של חוקי דה־מורגן, ועל כן, היא מושארת כתרגיל לקורא.
| הפרק הקודם: יחסים בין קבוצות |
פעולות על קבוצות | הפרק הבא: מכפלה קרטזית |

















































