פיזיקה קוונטית 1 - מחברת קורס/הרצאה מספר 3

פיזור בראג (Bragg) - המשך

תזכורת: אנו דנים בפיזור בראג (Bragg) של גלים א"מ ע"י גביש:

הפרש הפאזה: $\ \delta ={\frac {2\pi }{\lambda }}\left({\bar {H_{0}M'}}+{\bar {M'H}}\right)$

$\ \left\{{\begin{matrix}{\bar {H_{0}M'}}={\bar {MM'}}\sin \left(\theta -\phi \right)\\{\frac {d}{\bar {M'M}}}=\cos \phi \end{matrix}}\right.\Rightarrow {\bar {H_{0}M'}}={\frac {d}{\cos \phi }}\sin \left(\theta -\phi \right)$

$\ \left\{{\begin{matrix}\phi +\theta +\gamma ={\frac {\pi }{2}}\\{\frac {\bar {M'H}}{\bar {M'M}}}=\cos \gamma \end{matrix}}\right.\Rightarrow {\bar {M'H}}={\bar {M'M}}\sin \left(\theta +\phi \right)$

$\ {\bar {H_{0}M'}}+{\bar {M'H}}={\frac {d}{\cos \phi }}\left[\sin \left(\theta -\phi \right)+\sin \left(\theta +\phi \right)\right]=2d\sin \theta$

$\Rightarrow \ \delta ={\frac {2\pi }{\lambda }}2d\sin \theta =2\pi n,\ n\in \mathbb {Z}$

$\Leftarrow$ וקיבלנו את תנאי ההתאבכות של בראג: $\ n\lambda =2d\sin \theta$

"גלי חומר": תכונות גליות של חלקיקים (דה ברולי de Broglie 1992)

דנו כבר בקשר שבין א"מ ומכניקה קלאסית - הדואליות של גל-חלקיק.
נתון חלקיק נקודתי כשלהו. מאפייניו:

1.	מסה	$\ m$
2.	תנע	$\ {\vec {p}}=m{\vec {v}}$
3.	אנרגיה קינטית	$\ E={\frac {p^{2}}{2m}}$

נגדיר עבורו אורך גל $\ \lambda _{m}$ באופן הבא:
גל מקיים: $\ {\vec {k_{m}}}={\frac {2\pi }{\lambda _{m}}}{\hat {n}}$, וכבר אמרנו קודם ש- $\ {\vec {p}}=\hbar {\vec {k_{m}}}$ $\left({\vec {k_{m}}}={\frac {\vec {p}}{\hbar }}\Leftarrow \right)$
$\ \lambda _{m}={\frac {2\pi }{k_{m}}}={\frac {2\pi }{p}}\hbar ={\frac {2\pi }{p}}{\frac {h}{2\pi }}={\frac {h}{p}}$

וקיבלנו את אורך גל דה-ברולי: $\ \lambda _{m}={\frac {h}{p}}$

צורת כתיבה נוספת: $\ \lambda _{m}={\frac {h}{mv}}={\frac {h}{\sqrt {2mE}}}$

דוגמא 1

מהו אורך גל דה-ברולי של חלקיק בעל מסה $\ m=10^{-9}g$ ומהירות $\ v=3\cdot 10^{8}{\frac {m}{sec}}$ ?
פתרון : ראשית נבצע המרה של יחידות:
$\ h=6.62\times 10^{-34}J\cdot sec=6.62\times 10^{-34}{\frac {kg\cdot m^{2}}{sec^{2}}}\cdot sec=6.62\times 10^{-31}{\frac {g\cdot m^{2}}{sec}}$
וכעת, נציב בנוסחה שמצאנו למעלה עבור אורך גל דה-ברולי:
$\ \lambda _{m}={\frac {h}{mv}}={\frac {6.62\times 10^{-31}{\frac {g\cdot m^{2}}{sec}}}{10^{-9}g\cdot 3\times 10^{8}{\frac {m}{sec}}}}={\frac {6.62\times 10^{-31}m}{0.3}}=2.2\times 10^{-30}m=2.2\times 10^{-20}{\dot {A}}$ כלומר, עבור חלקיק זה לא נוכל להבחין בתופעות גליות, כי אורך הגל האופייני שלו קטן מאוד (תופעות גליות ניתן לראות בסדר גודל של $\ 1{\dot {A}}$)

• • הערה חשובה: בוודאי שמתם לב, כי ראשית טיפלנו ביחידות, ורק לאחר מכן הצבנו את הנתונים בנוסחא. כאו הוא המקום לשוב ולהדגיש, כי לא ניתן להפריז בחשיבותן של היחידות בכל הנוגע לפיזיקה, וכי טעות ביחידות יכולה להוביל לבלבול ולטעויות רבות.

כדאי לדעת: חשוב לשים לב ליחידות בפיזיקה!

דוגמא 2

נתון אלקטרון בעל $\ E_{k}=150_{ev},\ m_{e}=1.16\times 10_{kg}^{-19}$. חשבו את $\ \lambda _{m}$.
פתרון :
$\ \lambda _{m}={\frac {h}{\sqrt {2mE}}}={\frac {6.62\times 10^{-34}J\cdot sec}{\sqrt {2*1.16\times 10_{kg}^{-19}*150_{ev}}}}=5.9\times 10^{-9}{\frac {J\cdot sec}{kg\cdot ev}}\simeq 1{\dot {A}}$ כלומר, קיבלנו סדר גודל בו כן נוכל להבחין בתופעות גליות.

משוואת גל במימד אחד

נתון מיתר חד מימדי. עבור רגע נתון $\ t$ כלשהו (עבור מיקום נתון $\ x$ כלשהו), הגל ייראה כך כפונקציה של המיקום (כפונקציה של הזמן):

משוואת הגל הכללית (במימד אחד) תיראה כך:

$\ v^{2}{\frac {\partial ^{2}y}{\partial x^{2}}}={\frac {\partial ^{2}y}{\partial x^{2}}}(*)$

פתרון מתמטי

פתרון כללי של $\ (*)$ מתקבל באופן הבא (לפירוט ראה כאן - מדח):
נסמן:

${\begin{matrix}p=x-vt&&q=x+vt\\&\Leftrightarrow &\\x={\frac {q+p}{2}}&&t={\frac {q-p}{2v}}\end{matrix}}$.

ואז, הנגזרות החלקיות תהיינה:
$\ {\begin{matrix}{\frac {\partial }{\partial x}}={\frac {\partial }{\partial p}}{\frac {\partial p}{\partial x}}+{\frac {\partial }{\partial q}}{\frac {\partial q}{\partial x}}={\frac {\partial }{\partial p}}+{\frac {\partial }{\partial q}}&\Rightarrow &{\frac {\partial }{\partial x^{2}}}={\frac {\partial }{\partial p}}+{\frac {\partial }{\partial q}}\\{\frac {\partial }{\partial t}}={\frac {\partial }{\partial p}}{\frac {\partial p}{\partial t}}+{\frac {\partial }{\partial q}}{\frac {\partial q}{\partial t}}=-v{\frac {\partial }{\partial p}}+v{\frac {\partial }{\partial q}}&\Rightarrow &{\frac {\partial }{\partial t^{2}}}=v^{2}\left({\frac {\partial }{\partial p}}-{\frac {\partial }{\partial q}}\right)\end{matrix}}$

נסמן: $\ y(p,q)=f(p)+\wr g1(q)dq=f(p)+g(q)\Leftarrow {\frac {\partial y}{\partial p}}=g_{1}(q)$

$\ \Rightarrow y(x,t)=f(x-vt)+g(x-vt)$

משמעות פיזיקלית, יחס הדיספרציה

נניח לרגע ש- $\ g\equiv 0$, כלומר פונקצית הגל נראית כך: $\ y(x,t)=f(x-vt)$ - כלומר גל הנע בכיוון ציר $\ {\hat {x}}$. לעומת זאת, אם $\ f\equiv 0$, כלומר $\ y(x,t)=g(x+vt)$, נקבל גל הנע בכיוון $\ -{\hat {x}}$.
גל כללי הוא סופרפוזיציה (=צירוף לינארי, הרכבה) של גלים כאלה.

המקרה הקנוני

נסמן:

A	= משרעת
$\ k={\frac {2\pi }{\lambda }}$	=מספר הגל
$\ \omega ={\frac {2\pi }{T}}$	=תדירות

$\ f(x-vt)=A\cos \left(k\left[x-vt\right]+\phi \right)=a\cos \left(kx-kvt+\phi \right)=$ $\ =a\cos \left({\frac {2\pi }{\lambda }}x-{\frac {2\pi t}{T}}+\phi \right)$
פונקציה זו נקראת "קנונית" משום שהיא מרכיבה כל גל אחר (כלומר כל גל הוא הרכבה של גלים כאלה).
אם אין פאזה $\ \left(\phi \right)$: $\ f(x-vt)=a\cos(kx-\omega t)$. ומתקיים:
$\ \left.{\begin{matrix}{\frac {\partial ^{2}}{\partial x^{2}}}f&=&-Ak^{2}\cos \left(kx-\omega t\right)\\{\frac {\partial ^{2}}{\partial t^{2}}}f&=&-A\omega ^{2}\cos \left(kx-\omega t\right)\end{matrix}}\right\}\underbrace {\Rightarrow } _{*}\omega =vk$ (כאשר ב-* הצבנו את משוואת הגלים).
הקשר $\ \omega =\omega (k)$ נקרא יחס הדיספרציה (נפיצות), ובאמצעותו ניתן תמיד לבנות את משוואת הגל.
ניזכר בהגדרות מחשמל וגלים: מהירות פאזה: $\ v_{p}\equiv {\frac {\omega }{k}}$, מהירות החבורה: $\ v_{g}\equiv {\frac {\partial \omega }{\partial k}}$. אם $\ \omega =vk$, נקבל: $\ v_{p}=v_{g}=v$.

דוגמא - חלקיק יחסותי

נתון חלקיק יחסותי $\ E={\sqrt {p^{2}c^{2}+m^{2}c^{4}}}$, ואמרנו שמתקיימים הקשרים הבאים: $\ E=\hbar \omega ,\ p=\hbar k$ $\ \Leftarrow \hbar \omega ={\sqrt {\hbar ^{2}k^{2}c^{2}+m^{2}c^{4}}}$ - וקיבלנו את יחס הדיספרסיה: $\ \omega ={\sqrt {k^{2}c^{2}+{\frac {m^{2}c^{4}}{\hbar ^{2}}}}}$.

• שימו לב! עבור $m=0$ נקבל את היחס $\ \omega =kc$, כלומר פוטון.
  

מהירות הפאזה (חסרת משמעות פיזיקלית, לכן יכול להיות גדולה מ-$\ c$): $\ v_{p}={\frac {\omega }{k}}=c{\sqrt {1+{\frac {m^{2}c^{2}}{\hbar ^{2}k^{2}}}}}\geq c$
מהירות החבורה (המהירות בה עוברת האנרגיה, כמובן $\ c\geq$): $\ v_{g}={\frac {\partial \omega }{\partial k}}={\frac {c}{\sqrt {1+{\frac {m^{2}c^{2}}{\hbar ^{2}k^{2}}}}}}\leq c$

דוגמא - גל חומר לא יחסותי

אנרגיה קינטית: $E={\frac {p^{2}}{2m}}$, וכן מתקיים: $\ p=\hbar \Rightarrow E={\frac {\hbar ^{2}k^{2}}{2m}}$. מאידך: $\ E=\hbar \omega$ $\ \hbar \omega ={\frac {\hbar ^{2}\omega ^{2}}{2m}}\Leftarrow$.
ומכאן קל למצוא את יחס הדיספרציה:

$\ \omega ={\frac {\hbar k^{2}}{2m}}$

המהירויות: $\ v_{p}={\frac {\hbar k}{2m}},\ v_{g}={\frac {\hbar k}{m}}$. במקרה זה, $\ v_{g}=2\cdot v_{p}$.

סופרפוזיציה של גלים מישוריים: חבורת גלים

משפט: כל פתרון של משוואת הגלים הינו סופרפוזיציה של גלים הרמונים מישוריים, אפילו גל כזה:

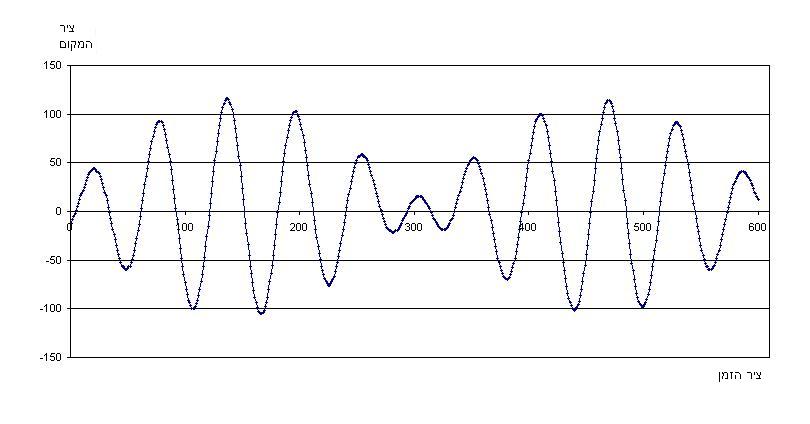
• דוגמא : פעימות של שני גלים הרמוניים:
  

$\ \left\{{\begin{matrix}y_{1}(x,t)=a\cdot \cos \left(k_{1}x+\omega t\right)\\y_{2}(x,t)=a\cdot \cos \left(k_{2}x+\omega t\right)\end{matrix}}\right.$

$\ y(x,t)=y_{1}(x,t,)+y_{2}(x,t)=2a\cdot \cos \left({\frac {1}{2}}\left(k_{1}+k_{2}\right)x+\omega t\right)\cdot \ cos\left({\frac {1}{2}}\left(k_{1}-k_{2}\right)x\right)$ עם גל זה התעסקנו רבות בקורס מכניקה - חשמל וגלים, לכן כולנו יודעים איך הוא נראה:

(...המשך בשיעור הבא...)

ההרצאה הקודמת: הרצאה מספר 2

עמוד ראשי: פיזיקה קוונטית 1 - מחברת קורס

ההרצאה הבאה: הרצאה מספר 4