הקדמה

בקצרה קשה להסביר מהו אינטגרל. ניתן לומר כי הוא ביטוי לשתי פעולות שונות הרלוונטיות לנו :

הפונקציה הקדומה או האינטגרל הלא־מסוים - פעולה הפוכה לגזירה במילים אחרות, מציאת הפונקציה באמצעות הנגזרת שלה.
האינטגרל המסוים - מספר השווה לשטח הכלוא בין ציר ה־ $\ x$ לבין גרף הפונקציה, בין קצות הקטע.

אינטגרציה: במהלך השנים היו ניסיונות רבים בידי מתמטיקאים לחשב שטח של צורות עקומות. ניסיונות אלו הובילו לפיתוח של שיטה ששמה "אינטגרציה" במהלכה מיצרים מלבנים רבים או חצי מלבנים (משולשים) עמם ניתן לחשב באופן המקורב ביותר את השטח של עקומה.

נגזרת (שיפוע המשיק): מנגד מתמטיקאים רבים נסו למצוא את שיפועו של עקומה (=נגזרת). בעוד בפונקציה לינארית (קו ישר), לה יש שיפוע שאינו משתנה מנקודה לנקודה וניתן לחישוב באמצעות ההפרש של שתי נקודות ( ${\displaystyle m={\frac {y_{1}-y_{2}}{x_{1}-x_{2}}}}$ ), אצל שאר הפונקציות ניתן להעביר מספר מיתרים מנקודת ההשקה ולקבל ערך שיפוע שונה. הפתרון היה חישוב שיפוע משיק הנמצא בין שני נקודות על העקומה שקרובות זו לזו. תהליך זה נקרא גזירה.

במשך שנים שתי פעולות אלו נחשבו שונות זו מזו. בסוף המאה ה-17, ניוטון ולייבניץ הוכיחו בתיאוריה הקרויה "המשפט היסודי של החשבון הדיפרנציאלי והאינטגרלי" (משפט ניוטון-לייבניץ ) כי שני התהליכים האלו קשורים זה לזה: תהליך האינטגרציה (מציאת שטח מתחת לגרף) הוא תהליך הפוך לגזירה (מציאת שיפוע העקומה). פרצה דרך זו העניקה למתמטיקאים כלים נוספים לבצע אינטגרציה - חוקי הנגזרת.

עתה נרחיב על שתי הפעולות בנפרד.

הפונקציה הקדומה

פונקציה קדומה ( $F(x)$ ), היא הפונקציה הראשונית לפני "הגזירה", אותה מקבלים לאחר האינטגרציה. דהינו, זוהי הפונקציה הראשונה אותה גזרו $F(x)={\frac {x^{3}}{3}}$ וקיבלו נגזרת מסוימת, "פונקציה חדשה" $f'(x)=x^{2}$ .

טענה 1: פונקציה קדומה

פונקציה $F(x)$ נקראת פונקציה קדומה של $f(x)$ בקטע כלשהו, אם לכל נקודה בקטע $F'(x)=f(x)$ . כלומר $f(x)$ היא הנגזרת של $F(x)$ בקטע.

לנגזרת יכולות להיות מספר פונקציות קדומות, להבדיל מפונקציה לה יש נגזרת אחת.

דוגמה 1: נגזרות קודמות לפונקציה

עבורה הנגזרת $F'(x)=x^{2}$ יכולות להיות הפונקציות: $f(x)={\frac {x^{3}}{3}}$ , $f(x)={\frac {x^{3}}{3}}+1$ , $f(x)={\frac {x^{3}}{3}}+2$ וכן הלאה.

בכדי לייצג את כלל הפונקציות נעזרים באינטגרל הבלתי מסוים. האינטגרל הבלתי מסוים מייצג את האיבר החופשי $(1,2,3)$ באמצעות קבוע האינטגרציה המסומן באות C : $f(x)={\frac {x^{3}}{3}}+C$ .

אינטגרל לא-מסוים הוא ביטוי לכל הפונקציות הקדומות.

מציאת C

בכדי למצוא את C נזדקק לנקודה דרכה עוברת הפונקציה הקדומה. אם תהיה לנו נקודה, נוכל להציב את x וy במשוואת האינטגרל ולקבל משוואה בנעלם אחד (c). דוגמה: נתונה הפונקציה $f(x)=x^{2}+{\frac {1}{\sqrt {x}}}+3$ ונתונה נקודה על האינטגרל של הפונקציה: (3,6). צריך לחשב את האינטגרל בדיוק.

פיתרון: נחשב את האינטגרל הלא-מסוים:

$\int \left(x^{2}+{\frac {1}{\sqrt {x}}}+3\right)dx={\frac {x^{3}}{3}}+2{\sqrt {x}}+3x+c$ .

כעת נציב את ערכי הx והy שנתונים:

${\frac {3^{3}}{3}}+2{\sqrt {3}}+3\cdot 3+c=18+2{\sqrt {3}}+c=6\Rightarrow c=-12-2{\sqrt {3}}=-25.73$

פרק זה לוקה בחסר. אתם מוזמנים לתרום לוויקיספר ולהשלים אותו. ראו פירוט בדף השיחה.

אינטגרל המסוים

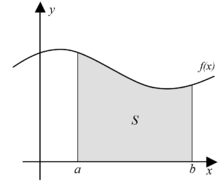
כאמור אינטגרל הוא גם ביטוי לשטח הכלוא בין פונקציה קדומה לציר ה- $x$ דהינו זהו ההפרש בין אינטגרל בנקודה מסוימת לאינטגרל בנקודה אחרת (=אינטגרל מסוים).

הנגזרת היא שיפוע מכאן שהיא מבטאת את : $m=f'(x)={\frac {y_{1}-y_{2}}{x_{1}-x_{2}}}$ ובמילים אחרות : $m=f'(x)={\frac {dy}{dx}}$ (דלתא $\Delta$ = הפרש).

כדאי למצוא את $y=F'(x)$ (הנגזרת של פונקציה קדומה) צריך לבצע אינטגרציה ל- $f(x)$ (לפונקציה חדשה) דהינו לחשב את $F'(x)={\frac {dy}{dx}}$ .

על פי כלל הנגזרת הקדומה, כפי שהוצגה לעיל, $F(x)'=f(x)$ ולכן ${\frac {dy}{dx}}=f(x)$

נוכל לרשום $dy=f(x)*dx$ .

נבצע אינטגרציה לשני האגפים ונקבל $y=\int f(x)dx$ (לא ניתן לבצע לצד השמאלי אינטגרציה ללא ערכי תחום).

לכן נוכל לומר $\int {f(x)dx=F(x)+c}$ כאשר $F'(x)=f(x)$

הקשר בין פונקציה קדומה לאינטגרל

נמצא את השטח הנמצא באיור בין הנקודות $S_{aA}$ (מתחת לפונקציה) ונוכיח באמצעותו את הקשר בין הפונקציה הקדומה לאינטגרל.

נחשב את השטח תחילה באמצעות יצירת מלבן אותו יהיה לנו קל לחשב.

נבחר נקודה הקרובה ביותר אל $A$ (באיור סימנו את נקודה זו כ- $B$ על אף שמרוחקת מנקודה $A$ בכדי להקל על ההסבר בהמשך)

נוריד אנכים מהנקודות $A$ ו- $B$ .

גודל האנכים $h_{A},h_{B}$ זהה לערך ה- $y$ של הנקודות דהינו $h_{A}=yA$ ו- $h_{B}=y_{B}$ .

המרחק בין הנקודה $C,D$ הוא ההפרש בין ערכי ה- $x$ של הנקודות $A$ ו- $B$ דהינו $x_{A}-x_{b}$ (לכן בדרך כלל נהוג לסמן את הנקודות לא באותיות C ו-D אלא $x,x_{1}$ כפי שננהג מעתה)

נניח כי הנקודה $a$ היא נקודה קבועה עבור כלל הפונקציות על כן גודל שטח הפונקציות תלוי במיקום של הנקודה $A$ .

אם הנקודה $A$ תנוע קדימה כך גם הנקודה $B$ ששואפת להיות צמודה אליה ולפיכך יש לנו שני שטחים שעלינו לחשב בין הנקודות $S_{aC}+S_{CD}$ . מכאן השטח הקטן שווה $S_{aC}=S_{aD}-S_{CD}$

נעביר שני ישרים המקבילים לנקודות $A$ ו- $B$ :

$S_{BDCF}=x_{1}*(x-x_{1})$

$S_{EDCA}=x_{A}*(x-x_{1})$

השטח הכלוא בין גרף הפונקציה לבין הנקודות $A$ ו- $B$ קטן משטח המלבן שנוצר כאשר מעבירים מקביל לציר ה- $x$ מהנקודה $B$ כלומר, $S_{CD}<S_{BCDF}$

השטח הכלוא בין גרף הפונקציה לבין הנקודות $A$ ו- $B$ גדול משטח המלבן שנוצר כאשר מעבירים מקביל לציר ה- $x$ מהנקודה $A$ כלומר, $S_{CD}>S_{CDAE}$

במידה והפונקציה הייתה קבועה השטחים היו יכולים להיות שווים לשטחי המלבנים ועל כן ניתן לכתוב

$S_{BCDF}\geq S_{CD}\geq S_{CDAE}$

נציב באי השוויון את ערך השטחים ונקבל: $f(x)(x-x_{1})]\leq S_{CD}\leq f(x_{1})(x-x_{1})$

$S_{CD}=S_{x}-S_{x_{1}}$

$f(x)(x-x_{1})\leq S_{x}-S_{x_{1}}\leq f(x_{1})(x-x_{1})$

נחלק ב- $(x-x_{1})$ ונקבל $f(x)\leq {\frac {S_{x}-S_{x_{1}}}{(x-x_{1})}}\leq f(x_{1})$

אנו שואפים כי $x$ יהיה במרחק הקטן ביותר מ- $x_{1}$ על כן נוכל "לכתוב" $f(x_{1})\leq {\frac {S_{x_{1}}-S_{x_{1}}}{(x_{1}-x_{1})}}\leq f(x_{1})$

הביטוי החדש שמתקבל הוא למעשה זהה להגדרת הנגזרת ובמילים אחרות נוכל להציב $f(x_{1})\leq S'_{aCB}\leq f(x_{1})$

על פי כלל הסנוויץ (אם ביטוי גדול או שווה וקטן שווה לביטוי אזי הוא שווה לביטוי) נקבל $leS'_{aCB}=f(x_{1})$ כלומר קבלנו שפונקציה שווה לשטח הנגזרת שלה

קיבלנו שהשטח מתחת לפונקציה הוא הפונקציה הקדומה של הפונקציה. כעת נמצא את c:

נבחר פונקציה קדומה אחרת, $F(x)$ , ונראה מה קורה כשמציבים $x=a$ . כמובן שבנקודה הזו פונקצית השטח שווה לאפס, ולכן נקבל:

$S_{ax}=F(x)+c\Rightarrow F(a)+c=0\Rightarrow c=-F(x)$ כלומר השטח שווה ל $S_{ax_{1}}=F(x_{1})-F(a)$ .

גודל הפונקציה היא סכום $\left(\int \right)$ השטחים ב- $\int _{a}^{x_{1}}\!\!f(x_{1})dx$

$f(x_{1})$ היא הפונקציה

$dx$ הוא הפרשי ה- $x$ . ניתן לחשב את השטחים גם על פי הפרשי ה- $y$ הרי $m=f'(x)={\frac {y_{1}-y_{2}}{x_{1}-x_{2}}}$ דהינו ${\frac {d_{y}}{d_{x}}}=f'(x)$

הערות שולים