פרק 1: ספין  והתהודה המגנטית.
והתהודה המגנטית.
רקע כללי וסקירה היסטורית:
[עריכה]ספין הינו מושג קשה להבנה, מאחר ואין לו שום מקביל קלאסי. כזכור, הפכנו את המושגים הקלאסיים לקונטיים ע"י כך שהעברנו משתנים וגדלים לאופרטורים. זכור מכולם הוא משפט ארן-פסט, המראה את הקשר ההדוק שבין גדלים קלאסיים לבין אופרטורים וממוצעים קוונטיים.
כמו כל תופעה קוונטית, גם את הספין גילו באמצעות ניסויים ומדידות, שתוצאותיהם לא התאימו לתיאורית שכבר היו קיימות. נתאר להלן 3 מהם:
- ב- 1925 ביקש Unlenbeck (הפיזיקאי) מחברו ההיסטוריון Gandsmit לעזור לו בניסוי הקשור במדידת וניתוח ספקטרום אטום המימן. כזכור. את אטום המימן ניתן לנתח תיאורטית באופן מדוייק מאוד. הזוג ההולנדי גילה בניסוי פיצול של קווים ספקטרלים במקום בו לא אמור להיות כזה.
- אפקט זימן: אם שמים אטום בשדה מגנטי קבוע והומוגני (לא כמו בניסוי שטרן-גרלך!!!) מקבלים פיצול של הקוים הספקטראלים למס' נתון (n מסויים). כזכור מהסמסטר שעבר, עבור תנ"ז אורביטלי נקבל
 קווים, ומאחר ו-
קווים, ומאחר ו-  נקבל מספר אי זוגי של קווים.
נקבל מספר אי זוגי של קווים.
בחלק מהתצפיות התקבל מספר זוגי של קוים, והחוקרים לא הציחו להבין מדוע ולמה.
3. כזכור, התנ"ז פרופורציוני למומנט המגנטי. עבור חלקיקים פשוטים, המדידות הראו מקדם אחר מאשר זה שחושב בתיאוריה (כאשר "תיאוריה" פירושה: ניתוח אטום המימן, מ"ש (משוואת שרדינגר) ושאר דברים שכבר היו ידועים אז).
חיפוש מקבילה קלאסית לספין
[עריכה]אלקטרון הוא החלקיק עימו נעבוד, לפחות בהתחלה.
יש המכנים את ספין ה-  של האלקטרון בשם "תנ"ז בלתי נפרד". זוהי הגדרה בעייתית, מאחר והספין אינו מתאר שום תנועה קלאסית - לא סיבובית ולא אחרת.
של האלקטרון בשם "תנ"ז בלתי נפרד". זוהי הגדרה בעייתית, מאחר והספין אינו מתאר שום תנועה קלאסית - לא סיבובית ולא אחרת.
- עבור מי שעדיין לא השתכנע, להלן דוגמה הממחישה מדוע ניסיון למצוא לספין הקבלה קלאסית לא יצליח:
נתאר אלקטרון ככדור בעל רדיוס ![{\displaystyle \ R\cong 10^{-8}[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba9f2fd480bcf1741d22ae1abb9735b9a7cfe9e2) , ונבחר בהקבלה הקלאסית הבאה:
, ונבחר בהקבלה הקלאסית הבאה:
נפרש את הספין כתנועה סיבובית מסביב לציר מסויים. (כיוון התנועה:  )
)
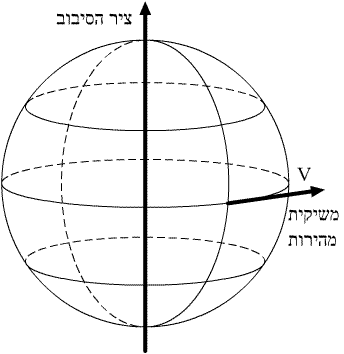
נתון: ספין  , ובהקבלה לתנ"ז אורביטלי
, ובהקבלה לתנ"ז אורביטלי  נקבל:
נקבל:

כאשר  = התנ"ז של הספין (בהקבלה לקלאסית), כלומר הסיבוב כתוצאה מהספין.
= התנ"ז של הספין (בהקבלה לקלאסית), כלומר הסיבוב כתוצאה מהספין.
 נרצה לחשב את המהירות המשיקית:
נרצה לחשב את המהירות המשיקית:

(כאשר: * =  הינו מומנט ההתמד של האלקטרון).
הינו מומנט ההתמד של האלקטרון).

כיום, זוהי אחת הראיות לכך שלספין אין שום הקבלה קלאסית. פאולי, לעומת זאת, טען בזמנו שתוצאה זו מהווה טיעון מוחץ כנגד הרעיון של קיום ספין.
• חשוב להבהיר: לכל חלקיק יש ספין שונה!
למשל: עבור אלק', פרוטונים ונויטרונים (למשל) הספין =  . ישנם חלקיקים בעלי ספין
. ישנם חלקיקים בעלי ספין  , 1 (למשל פוטונים), 2 וכולי.
, 1 (למשל פוטונים), 2 וכולי.
 מהי המשמעות הפיזיקלית של הספין? - כרגע, זוהי פשוט תכונה של החלקיק, ממש כמו שמסה ומטען, למשל, הם תכונות של חלקיקים.
מהי המשמעות הפיזיקלית של הספין? - כרגע, זוהי פשוט תכונה של החלקיק, ממש כמו שמסה ומטען, למשל, הם תכונות של חלקיקים.
חשוב לציין, כי מעולם לא נמצאה הוכחה לקיומו של הספין, או לאי קיומו. פשוט, תיאורית הספין מתאימה לניסויים ולתצפיות, וכל מי שרוצה מוזמן לנסות ולהפרך אותה, או למצוא תיאוריה "טובה יותר" (או מדויקת יותר). כמו כן, קביעת ערך הספין נעשתה על סמך ניסויים, כי הפיזיקה כמו בפיזיקה - התיאוריה המתאימה לניסויים היא זו שתתקבל.
מעניין לשים לב, אם כן, שהערך  עבור אלקטרון קשור לטרנספורמצית לורנץ וליחסות פרטית (ועל כך - בפרקים הבאים).
עבור אלקטרון קשור לטרנספורמצית לורנץ וליחסות פרטית (ועל כך - בפרקים הבאים).
מרחב הילברט של ספין 1/2
[עריכה]נשתמש באותה האלגברה בה אנו משתמשים ע"מ לתאר את  (כאן המקום לציין, שוב, שפרט לעובדה ששני המושגים משתמשים ומוגדרים ע"י אותה האלגברה, אין ביניהם שום קשר!)
(כאן המקום לציין, שוב, שפרט לעובדה ששני המושגים משתמשים ומוגדרים ע"י אותה האלגברה, אין ביניהם שום קשר!)
נתאר את הספין, כצפוי, בעזרת אופרטורים:  .
.
תזכורת: מדידה = הפעלת אופרטור על מצב:  .
.
ניזכר לרגע באלגברה של התנ"ז  (ובאלגברה בלבד! לא בשום דבר אחר שקשור אליו!): עבור
(ובאלגברה בלבד! לא בשום דבר אחר שקשור אליו!): עבור  נתון, ניתן לקבל
נתון, ניתן לקבל  ערכי
ערכי  , והערכים הנמדדים יהיו
, והערכים הנמדדים יהיו  .
.
עבור ספין  :
:  , לכן נוכל למדוד אחד משני ערכים:
, לכן נוכל למדוד אחד משני ערכים:  . נסמן לכן:
. נסמן לכן:  .
.
- מהם יחסי החילוף של הספינים? כמו בתנ"ז, גם כאן מתקיים:

כזכור, קשר זה מגדיר את אלגברת הלי של החבורה.
- מימד מרחב ההילברט שלנו: 2, כי יש לנו 2 מצבי מדידה אפשריים.
כזכור, נרצה שוקטורי הבסיס יהיו מ"ע (מצבים עצמיים) המתאימים לאופרטורים לכסינים (C.S.C.O). בדומה ל-  , נגדיר את הבסיס
, נגדיר את הבסיס  ע"י מ"ע של
ע"י מ"ע של  באופן הבא:
באופן הבא:

כאשר, כמו בתנ"ז, פירוש המצבים הינו:

בהפעלת האופרטורים  על איברי הבסיס נקבל:
על איברי הבסיס נקבל:

כאן לא נסביר מהיכן התוצאות הללו מגיעות. מי שמעוניין, מוזמן להסתכל במחברת מהסמסטר שעבר.
מצבים במרחב הספין והצגה מטריציונית שלהם
[עריכה]מצב כללי במרחב הספין נתון ע"י :  , וכמובן חייב לקיים:
, וכמובן חייב לקיים:
- נרמול:
 (אחרת נקבל, רחמנא ליצלן, מצב לא פיזיקלי!)
(אחרת נקבל, רחמנא ליצלן, מצב לא פיזיקלי!)
- המקדמים בריבוע הם ההסתברות למדוד למצוא את החלקיק במצב ספין מסויים, כלומר:

* הצגה מטריציונית של מצבים:
נגדיר:  , ואז מצב כללי של חלקיק במרחב הספין ירשם כ-
, ואז מצב כללי של חלקיק במרחב הספין ירשם כ-  .
.
ניזכר במטריצות פאולי:
 , ונזכור גם ש-
, ונזכור גם ש-  מקיים:
מקיים:
 .
ובייחד עם התכונה
.
ובייחד עם התכונה  נסיק:
נסיק:

נרצה כעת להציג את המ"ע של  ושל
ושל  בבסיס זה:
בבסיס זה:

וכמובן ש-  מתחלפים עם
מתחלפים עם  .
.
הצגה בקואורדינטות כדוריות
[עריכה]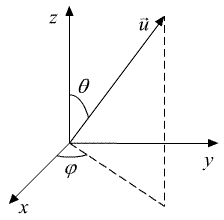 כאשר:
כאשר:  (כרגיל - הפוך ממתמטיקה!)
(כרגיל - הפוך ממתמטיקה!)
נתון וקטור  כלשהו במרחב. אזי, ניתן לרשום אותו באופן הבא:
כלשהו במרחב. אזי, ניתן לרשום אותו באופן הבא:
 כאשר
כאשר  וקטורי יחידה של הצירים
וקטורי יחידה של הצירים  בהתאמה.
בהתאמה.
הטלה של  על (לאורך) הציר
על (לאורך) הציר  :
:
 (כמו שעשינו בעבר עבור
(כמו שעשינו בעבר עבור  )
)
• כל מצב כללי של ספין ניתן לרישום כמ"ע של  לאורך ציר מסויים. למשל, לאורך ציר
לאורך ציר מסויים. למשל, לאורך ציר  , המצב העצמי ייראה כך:
, המצב העצמי ייראה כך:
 ,
,
ומתקיים: 
 נשים לב לנקודה מעניינת: מצד אחד, אמרנו תמיד שפאזה אבסולוטית הינה חסרת משמעות כאשר אנו מבצעים מדידה. מצד שני, עבור
נשים לב לנקודה מעניינת: מצד אחד, אמרנו תמיד שפאזה אבסולוטית הינה חסרת משמעות כאשר אנו מבצעים מדידה. מצד שני, עבור  קיבלנו ע"ע שונה מאשר זה שקיבלנו עבור
קיבלנו ע"ע שונה מאשר זה שקיבלנו עבור  , אע"פי שההבדל בין המצבים הינו כפל בפאזה
, אע"פי שההבדל בין המצבים הינו כפל בפאזה  בלבד!
בלבד!
הערה חשובה: כל האמור לעיל נכון אך ורק עבור ספין  !!! לא עבור ספין כללי!!!
!!! לא עבור ספין כללי!!!
![]() )
)

 כאשר: (כרגיל - הפוך ממתמטיקה!)
כאשר: (כרגיל - הפוך ממתמטיקה!) 



![{\displaystyle \ R\cong 10^{-8}[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba9f2fd480bcf1741d22ae1abb9735b9a7cfe9e2)























































