דוגמה לעקרון אי-הוודאות של הייזנברג
[עריכה]ניקח גל מישורי סטנדרטי: 
נגדיר:  - זהו גל מישורי יחיד עם מספר גל
- זהו גל מישורי יחיד עם מספר גל  . נזכור שמתקיים:
. נזכור שמתקיים:  , כלומר לגל זה ישנה תדירות מסויימת ויחידה.
, כלומר לגל זה ישנה תדירות מסויימת ויחידה.
יהא כעת ![{\displaystyle \ k\in [k_{1},k_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0575acb821bbf4cf6d1a484113352c46e3e090ff) , ונרצה להרכיב מספר אינסופי של גלים מישוריים בעלי רצף התדירויות הנ"ל. נבנה זאת באופן הבא:
, ונרצה להרכיב מספר אינסופי של גלים מישוריים בעלי רצף התדירויות הנ"ל. נבנה זאת באופן הבא:
 , (כאשר
, (כאשר  = סכימה על רצף תדירויות ו-
= סכימה על רצף תדירויות ו-  = עבור תדירות מסויימת)
= עבור תדירות מסויימת)



מתקיים:  . נסמן:
. נסמן:  , ונקבל:
, ונקבל: 
 .
.
וכל מי שאי פעם למד גלים יודע שגרף הפונקציה נראה כך:
 נסמן:
נסמן:  ., ונרצה ללמוד משהו על הקשר בינו לבין
., ונרצה ללמוד משהו על הקשר בינו לבין  (שהוא, כזכור, טווח בתדירויות שלנו). לשם כך, נבדוק מתי הסינוס מתאפס:
(שהוא, כזכור, טווח בתדירויות שלנו). לשם כך, נבדוק מתי הסינוס מתאפס:

 עבור
עבור  מסויים.
מסויים.
נתבונן בגרף: עבור הנקודה  , מתקיים:
, מתקיים:  , ואילו עבור הנקודה
, ואילו עבור הנקודה  , מתקיים:
, מתקיים:  . נחסר את שני אלה, ונקבל:
. נחסר את שני אלה, ונקבל:

 |
וקיבלנו:

|
כלומר: אם נרצה לקבל  יותר גדול, יהא עלינו לקחת
יותר גדול, יהא עלינו לקחת  יותר קטן, ולהיפך. זוהי דוגמא לעיקרון אי-הוודאות, ויותר מאוחר נראה את הקשר בין עקרון זה לבין התמרת פוריה.
יותר קטן, ולהיפך. זוהי דוגמא לעיקרון אי-הוודאות, ויותר מאוחר נראה את הקשר בין עקרון זה לבין התמרת פוריה.
הרכבה של גלים מישוריים (באופן כללי)
[עריכה]כאמור, אסכמת (אינטגרל) של גלים מישוריים בתחום התדרים ![{\displaystyle \ \left[k_{1},k_{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c594d1cc1c823d4d2ab131aaa400b280304c3a5a) תראה כך:
תראה כך:  . מדובר בהרכבה (סופרפוזיציה, צירוף לינארי), כאשר לכל
. מדובר בהרכבה (סופרפוזיציה, צירוף לינארי), כאשר לכל ![{\displaystyle \ k\in \left[k_{1},k_{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0213db827413a1027cfa403cb9c0b50bfa06eb51) המקדם של הפונקציה הוא
המקדם של הפונקציה הוא  .
.
כעת: לכל  נתאים מקדם
נתאים מקדם  כלשהו.
כלשהו.  שונה מ-
שונה מ-  ל-
ל-  , והוא מהווה פונקצית משקל עבור הגל בעל המאפיין
, והוא מהווה פונקצית משקל עבור הגל בעל המאפיין  . במילים אחרות,
. במילים אחרות,  הוא המקדם של האיבר ה-
הוא המקדם של האיבר ה-  -י, כפי שהוסבר בתחילת ההרצאה הקודמת.
-י, כפי שהוסבר בתחילת ההרצאה הקודמת.
נרחיב כעת את גבולות האינטגרל לכל הישר הממשי, ומקדם הנרמול שלנו (המקדם שלפני האינטגרל - יותר מאוחר נראה מדוע הוא נקרא "מקדם נרמול") יהיה  . ואז חבורת הגלים שלנו תהיה:
. ואז חבורת הגלים שלנו תהיה:
 .
.
נציב  , ונקבל:
, ונקבל: 
בעזרת התמרת פוריה, נוכל להסיק מכאן כי:  .
.
הפונקציה  היא, כאמור, הרכבה של גלים מישוריים. לכן, קיימת תופעת התאבכות ,ונרצה לחקור אותה. על מנת לעשות זאת, נחפש את המקסימום של הפונקציה.
היא, כאמור, הרכבה של גלים מישוריים. לכן, קיימת תופעת התאבכות ,ונרצה לחקור אותה. על מנת לעשות זאת, נחפש את המקסימום של הפונקציה.
נניח שהפונקציה  היא גאוסיאנית. ואז, נוכל לכתוב אותה באופן הבא:
היא גאוסיאנית. ואז, נוכל לכתוב אותה באופן הבא:  .
.
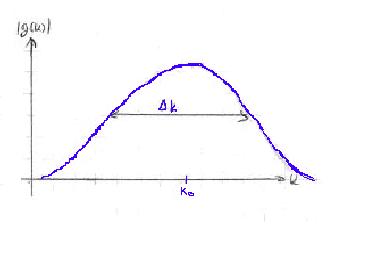
באופן כללי יתכן גם ש-  , אבל כרגע נניח שהוא קטן מספיק. אם כן, נוכל לקרב את הפאזה של
, אבל כרגע נניח שהוא קטן מספיק. אם כן, נוכל לקרב את הפאזה של  באמצעות טור טיילור באופן הבא:
באמצעות טור טיילור באופן הבא:
 , כאשר * = איברים שניתן להזניח.
, כאשר * = איברים שניתן להזניח.

נסמן:
 .אז נקבל:
.אז נקבל:




כעת: נשים לב ש-  הוא מספר, וש-
הוא מספר, וש-  לא תלוי ב- k - כלומר אפשר להוציא אותו מחוץ לאסכמת. ונקבל:
לא תלוי ב- k - כלומר אפשר להוציא אותו מחוץ לאסכמת. ונקבל:

נסמן:  , ונרצה לחקור את ההתנהגות של A.
, ונרצה לחקור את ההתנהגות של A.
 נסמן: ., ונרצה ללמוד משהו על הקשר בינו לבין (שהוא, כזכור, טווח בתדירויות שלנו). לשם כך, נבדוק מתי הסינוס מתאפס:
נסמן: ., ונרצה ללמוד משהו על הקשר בינו לבין (שהוא, כזכור, טווח בתדירויות שלנו). לשם כך, נבדוק מתי הסינוס מתאפס: 





![{\displaystyle \ k\in [k_{1},k_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0575acb821bbf4cf6d1a484113352c46e3e090ff)























![{\displaystyle \ \left[k_{1},k_{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c594d1cc1c823d4d2ab131aaa400b280304c3a5a)

![{\displaystyle \ k\in \left[k_{1},k_{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0213db827413a1027cfa403cb9c0b50bfa06eb51)






















