מתמטיקה תיכונית/הנדסת המרחב/זוויות בקוביה
הקדמה
[עריכה]מטרתו של פרק זה, היא לעזור למתקשים לראות את הזוויות הישרות שנוצרות בפאונים וכן, להבדיל בין הזוויות השונות שנוצרות. נדגים את הנושא בקוביה.
זווית בין אלכסון הפאון לאלכסון הבסיס (עליון/תחתון)
[עריכה]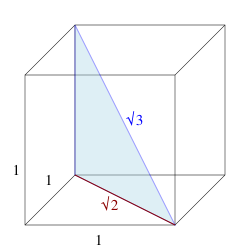
בין אלכסון הפאה לבסיס נוצרת זווית בין אלכסון הפאה לבסיס.
על פי המשפט : ישר ניצב למישור - אם ישר אנך לשני ישרים במישור, העוברים דרך עקבו, הוא אנך למישור (כלומר לכל ישר העובר במישור)
בקוביה, פאותיה אנכיות לבסיסים ולכן, ישר העובר בפאה, מאונך גם לישר העובר בבסיס. מכאן, שאלכסון הבסיס, אנך לכל אחד ממקצועי הפאה. במקרה שלנו, כיוון שמדובר בקוביה, אלכסון הקוביה חוצה אותה לשני "משולשי כסף" , ניתן לגלות את גודל אלכסון הבסיס באמצעות משפט פיתגורס . גובה הקוביה שווה לאחד, גם הוא.
נוצר משולש "אלכסון בסיס, אלכסון פאון ומקצוע" שאורך צלעותיו , נעזר במשפט פיתגורס
למעשה, כל קו שיחצה את אלכסון הבסיס ויצא מאחד הקודקוד הנמצא במרחב המקביל, יצור משולש ישר זווית.
-
זווית בין אלכסון פאה (בקוביה הפאה יכולה להיות בסיס) ואלכסון התיבה
-
זווית בין אלכסון פאה לבסיס
-
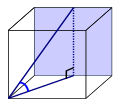
אלכסון מבסיס אחד אל בסיס שני הוא יתר במשולש בו הגובה וצלע הבסיס הם הניצבים
-
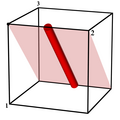
בדיוק כמו התמונה השניה. שימו לב, כל קו שנעביר על המרחב האדום יכול ליצור משולש ישר זווית (העברת קווים) שאורכם צלעותיו שווה לצלע הבסיס והגובה.
-
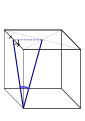
זווית בין אלכסון לבסיס
-
זווית בין אלכסון לפאה
מעל לכל חשוב לזכור את הזווית בכל אופן, בכל צורה - קירות הקוביה הם מאונכים זה לזה.
-
כותרת 1
-
כותרת 2
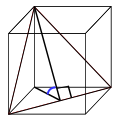
זווית בין אלכסון פאה ואלכסון תיבה
[עריכה]
בתרגילים תמצאו תיאורים מלבלבים (רגע מה הם אמרו? זה נתון? לא התרגיל אמור להיות קשה?) לזוויות שונות, חשבו לחלק את המשפט שנאמר:
- זווית.
- אלכסון פאה.
- אלכסון תיבה.
- איפה ה-? בין קירות הקוביה.
עוד זוויות
[עריכה]-
זווית בין שני מישורים
-
זווית בין אלכסוני התיבה
המלצות
[עריכה]- למי שהיה קשה לקלוט בעצמו ולמצוא את , רצוי לבנות קוביה (דגם) (להדפיס ולהדביק את הפאות "קירות" - תשאירו קצה להדבקה!). להעזר במקל וליצור אלכסונים תוך כדי מציאת הזווית . ה"משחק" עוזר להבין את אופן הממחשבה ומקבע את המידע במוח - לחוויה יש משקל חזק יותר על הזכרון.
- בכל פעם שמצירים קוביה, תיבה לצייר בפינה אחת -בגלל אופן הציור (ריבוע+מקבילית) אנו מאבדים את הזוויות החשובות.