מתמטיקה תיכונית/גיאומטריה אוקלידית/מיון משולשים על פי צלעות

משולש שווה שוקיים

משולש שווה שוקיים (מש"ש או משולש שו"ש) הוא משולש ששתיים מצלעותיו שוות בגודלן.

במשולש שווה שוקיים:

• השוקיים הן הצלעות השוות של המשולש.
• הבסיס הוא הצלע השלישית של המשולש.
• זוויות הבסיס הן הזוויות הצמודות לבסיס.
• זווית הראש היא הזווית שאינה צמודה לבסיס.

משפטים יחודיים למשולש שווה שוקיים:

• במש"ש זוויות הבסיס שוות (עפ"י החוק: מול צלעות שוות במשולש זוויות שוות).
• במש"ש הגובה לבסיס, חוצה הזווית לבסיס והתיכון לבסיס מתלכדים(מהווים ישר אחד).
• מול זוויות שוות מונחות צלעות שוות ולהפך

כיצד נוכיח שמשולש הוא שו"ש?

• משולש ששתיים מצלעותיו שוות הוא שו"ש עפ"י הגדרתו.
• משולש בו הגובה לאחת הצלעות הוא גם תיכון הוא שו"ש והצלע היא הבסיס.
• משולש בו הגובה לאחת הצלעות הוא גם חוצה זווית הוא שו"ש והצלע היא הבסיס.
• משולש בו חוצה הזווית הוא גם תיכון לצלע שממול לאותה זווית הוא שווה שוקיים והצלע היא הבסיס.
• משולש בו שתי זוויות שוות הוא שו"ש.

תרגול

משולש שווה צלעות

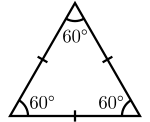
משולש שווה צלעות הוא משולש שכל צלעותיו שוות. כלומר: משולש שווה צלעות הוא למעשה משולש שווה שוקיים, שבו הבסיס שווה לשתי השוקיים. לפיכך, כל המשפטים שחלים על מש"ש חלים גם על משולש שווה צלעות(מש"ץ).

בנוסף לכך, במשולש שווה צלעות כל הזוויות שוות ל-60 מעלות. נוכיח זאת:

משולש שווה צלעות הוא למעשה משולש שווה שוקיים בו כל צלע יכולה לשמש כבסיס. לכן, לצורך העניין, נבחר ב-BC כבסיס. מכאן נובע כי זווית B שווה לזווית C(במש"ש זוויות בסיס שוות). כעת נבחר ב-AB כבסיס. נוכל להגיד כעת כי זווית A שווה לזווית B מאותה סיבה. נסיק כי כל הזוויות במשולש שוות עפ"י כלל המעבר. נסמן כל זווית ב-x ונסיק מהכלל, כי סכום כל הזוויות במשולש הוא 180 מעלות, כי $3x=180^{\circ }$ וכי $x=60^{\circ }$. כלומר: כל זווית במשולש שווה צלעות היא בת 60 מעלות.

כיצד נוכיח כי משולש הוא שווה צלעות?

• משולש שכל צלעותיו שוות הוא שווה צלעות.
• משולש ששתיים מצלעותיו שוות וזווית אחת בו שווה 60 מעלות הוא משולש שווה צלעות.

משולש שונה צלעות

כיתוב תמונה

פרק זה לוקה בחסר. אתם מוזמנים לתרום לוויקיספר ולהשלים אותו. ראו פירוט בדף השיחה.