חשבון אינפיניטסימלי/מושגים בסיסיים בתורת הקבוצות/נספח
הוכחת הטענה: הינה קבוצה בת מניה
[עריכה]כפי שאמרנו בפרק זה, על מנת להוכיח את הטענה עלינו למצוא לקבוצה סידור לפי סדר מסויים.
הוכחה: נראה עבור רציונלים חיוביים, ואז נוכל, לפי אותו הסדר, לסדר גם את השליליים (בדיוק כמו שעשינו עם ).
נסדר את המספרים הרציונלים בתוך טבלה גדולה בסדר הבא:
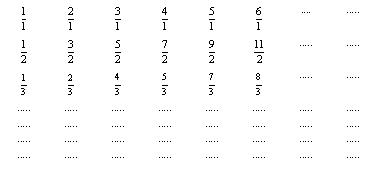
נסמן כעת מסלול בעזרת חיצים, באופן הבא:
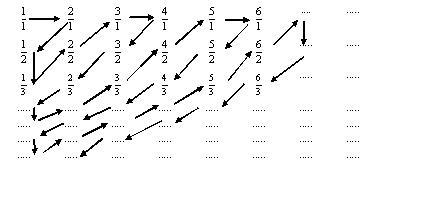
נלך כעת במסלול המסומן באמצעות החצים, ואז נוכל למנות אותם (כלומר: להגיד מי ראשון, מי שני וכולי). ▪
הוכחת הטענה: אינה קבוצה בת מניה
[עריכה]הוכחה: מספיק שנוכיח עבור קטע קטן מ- (שהרי אם קטע מקבוצה מסויימת אינו בר מניה, ודאי שהקבוצה כולה אינה כזו!). לכן, נוכיח רק עבור הקטע :
נניח בשלילה ש- הינו בר-מניה. כלומר, נוכל לסדר את האיברים בשורה: (כאשר המספרים אינם מציינים חזקה, אלא את מיקום המספר בשורה). ונוכיח שקיים מספר אחד לפחות בקטע שאינו ברשימה. נרשום כל אחד מהמספרים שברשימה בצורה עשרונית: (המספרים שברשימה מסמלים את הספרות ):
נבנה כעת את המספר באופן הבא: , כאשר נגדיר:
. כלומר, המספר החדש יהיה תמיד שונה בספרה אחת לפחות מכל מספר שברשימה (הוא יהיה שונה מהאיבר ה- במקום ה- )
אינו מופיע ברשימה הקטע אינו בר מניה.
וכאמור למעלה: ואינו בר מניה כולו אינו בר-מניה.
▪
הערות:
- שיטה זו (בה הוכחנו ש- אינו בן-מניה) נקראת שיטת האלכסון של קנטור, ע"ש קנטור ממציא השיטה ומשום שבשיטה זו אנו יוצרים איבר חדש, השונה מכל האיברים הקיימים, הנוצר באלכסון.
- אנחנו מתבססים ללא הוכחה על העובדה שכל מספר ממשי ניתן להצגה לכל היותר בשתי צורות כפיתוח עשרוני, והמספרים היחידים שניתנים להצגה כפולה שכזו הם מספרים שנגמרים ב- בהצגה אחת וב- בשנייה. בבירור המספר שבנינו אינו כזה, ולכן אין חשש שבנינו את אחד מהמספרים שכן הופיעו ברשימה בצורה שלו שלא הופיעה ברשימה.
- עוד על קבוצות בנות-מניה ושאינן בנות מניה, על שיטת האלכסון של קנטור ועוד - בקורס תורת הקבוצות.
בחזרה לקורס לחצו כאן.
























