רשתות נוירונים - מחברת קורס/הרצאה מספר 1

פרק 1 – מודל חשמלי של פעילות עצבית

מדוע כלול הקורס 'רשתות נוירונים' בתכנית הלימודים של מדעי המוח? ובכן, בין האנשים האחראים לכך ניתן למנות את קאמילו גולג'י ואת סנטיאגו רמון-י-כחאל, שמצאו כי המוח מורכב מתאים. תאים אלה - תאי עצב, או נוירונים - נתגלו ע"י סיר צ'ארלס סקוט שרינגטון מקושרים זה בזה באמצעות סינפסות. בעקבותיו מצא סיר ג'ון אקלס כי כל תא צובר קלטים דרך הסינפסות הרבות שבדנדריטים, ואילו סיר אלאן הודג'קין וסיר אנדרו האכסלי מצאו כי הצטברות מספקת של יונים בגוף התא בעקבות קלטים אלה גורמת לזרימת פוטנציאל פעולה דרך האקסון של התא אל הסינפסות. עקב זאת, כך מצא סיר ברנארד כץ, משתחררים שם נוירוטרנסמיטרים הנקלטים בתאים המקושרים לאקסון זה.

די בתיאור זה כדי להניח שהמוח מורכב מתאים רבים שכל אחד מהם קולט מסרים כלשהם מן התאים השכנים ברשת, ובהתאם למסרים אלה מפיק פלט הנקלט בתאים הקשורים לו, וכל זה על בסיס פעילות חשמלית הרוחשת בתאים. מהו הקלט הדרוש לתא כדי להפיק פלט מסויים? כמה פוטנציאלי פעולה יפיק התא כתוצאה מכמות מדודה של יונים שזרמו אליו דרך הדנדריטים?

אם נזריק זרם חשמלי באמצעות טפיפית לתוך נוירון מצוי מקליפת המוח, ונמדוד את קצב ירי פוטנציאלי הפעולה של התא, ניווכח כי נדרש זרם סף כדי לעורר את התא לירי, וכל עלייה בזרם, I, מעבר לסף זה תעלה את קצב הירי, f, עד לגבול כלשהו:

נוירונים אחרים ממקומות שונים במוח יכולים להניב קשרים אחרים, פשוטים או מורכבים יותר, בין זרם הקלט לבין קצב הירי. קצב זה קובע את כמות המסרנים העצביים שישתחררו מן התא, וכמות זו תשרה בהתאם זרמים חשמליים בתאי המטרה של התא היורה. זרמים אלו יגיעו לגופי התאים וישפיעו שם כאותו זרם שהוזרק מן הטפיפית. כל שנותר כעת כדי לדעת איך המוח עובד הוא אך לדקדק בפרטי הפעילות החשמלית בתאי העצב, וזאת נעשה בפרק זה, החותם את חקר המח.

מודל חשמלי שווה-פוטנציאל של תא עצב

התא הביולוגי רוחש פעילות בתוך חלל סגור המוגדר על ידי קרום התא. הקרום עשוי שכבת שומן כפולה, שעוביה כ- 4nm, והוא מבדיל בין התווך החוץ-תאי לחלל התוך-תאי. חומרים הנפוצים חוצה לתא ובתוכו, אינם יכולים לעבור דרך קרום שומני זה. התערובת בחלל התוך-תאי כוללת בעיקר מים, חומצות גרעין וחומצות אמינו, חלבונים למיניהם, ויונים למכביר. היונים, חלקם בעלי מטען חיובי וחלקם בעלי מטען שלילי, אך השליליים עולים במספרם במעט על החיוביים, ועל כן, סך המטען הכללי בתא הוא שלילי. חוסר איזון זה גורם לדחיית מטענים שליליים לדפנות התא, שם הם מתרכזים, שכן אינם יכולים לפעפע בנקל אל מעבר לקרום. יתר על כן, ריכוז שכזה מן הצד הפנימי ימשוך וירכז כמות דומה של מטען חיובי בעברו הנגדי של הקרום. התרכזותם של מטענים, Q , משני עברי הקרום בצורה זו יוצרת מתח קיבולי בין התווך החוץ תאי לבין החלל הפנימי של התא.

הקרום מהווה, לפיכך, מעין קבל, המפריד בין התווך החוץ תאי, שם יש פוטנציאל חשמלי , לבין החלל הפנימי של התא, שם יש פוטנציאל חשמלי . הפרש הפוטנציאלים על פני הקבל מתכונתי למטען המרוכז בו, , לפי הקיבול, , המאפיין את הקרום:

Qc = (Vi - Vout) * C

מן הראוי לציין, שכמות המטען המתקבל לפי הפוטנציאלים השגרתיים בתא היא מסדר גודל של 1PC, ומתאימה לכ- 10^7 יונים. כמות זו בטלה במיליון ביחס לכמות היונים בתא, ועל כן גם אם תשתנה פי כמה בגלל שינויי מתח, לא תהיה לכך השפעה משמעותית על ריכוז היונים בתא או על תפקודם.

הקרום השומני אמנם אטום, אך שתולות בו תעלות חלבוניות, המאפשרות מעבר בררני ומותנה של יונים דרך הקרום. מספר התעלות הפתוחות למעבר יון מסוים בתנאים כלשהם יקבע את זרם היונים החוצה את הקרום. בתנאים אלה, תחושב מוליכות הקרום, G , לאותו יון , K , לפי תוספת הזרם, Ik delta , המתקבלת עם עלייה קטנה של המתח החשמלי בין שני עברי הקרום, כך:

< (math>\; Gk = \frac {\vartriangle Ik}{\vartriangle(Vin-Vout)} </math> (1.2

פתיחת תעלות מסוגים שונים של יונים אלה ואחרים באותה העת תסתכם להולכה כללית של הקרום:

(1.3) $G=\sum _{n=1}^{m}Gn$ בהינתן m סוגים שונים של יונים (נתרן, כלור, אשלגן, וכו').

נתאר לפיכך את הקרום כצירוף של מרכיב קיבולי, C , ומרכיב הולכה, G , המגשרים במקביל בין התווך החוץ-תאי לתווך התוך-תאי.

הסבר קצר על האיור

אם התא גדול ומסועף עד שיש הפרשי פוטנציאלים בין נקודות שונות בתא, יש לייצג כל איזור נבדל בקרום במערכת נגד-קבל משלו, ולקשר בין המערכות ברכיבי הולכה המייצגים את המוליכות החשמלית שבחלל התוך תאי.

נסבך עתה מעט את המודל לנוכח הפרשי ריכוזים של יונים משני צידי הקרום. הפרשי ריכוזים אלה נשמרים על ידי משאבות יונים הפועלות כל העת בתוך הקרום. הפרש ריכוזים של יון מסויים מהווה כוח מניע של אותו יון למעבר מצד הריכוז הגבוה לצד הריכוז הנמוך. זו הסיבה לשמירת הפרש פוטנציאלים משני עברי הקרום, גם במצב מנוחה של התא, למרות שזרם יכול לזלוג לכאורה דרך התעלות עד להשוואת פוטנציאלים. כוח מניע זה, E, שערכו נע סביב -70mV , אינו משפיע על ההתנהגות החשמלית של יונים ביחס לקרום אטום, אלא על זרימתם דרך התעלות. לפיכך, יוסף הכוח המניע למודל כמקור מתח, בטור עם הנגד:

Add caption here

מבנה הקרום משותף לכל התאים והמינים השונים, ועל כן ערכו של הקיבול הקרומי די קבוע, ועומד על כ- 10nF לכל מילימטר רבוע של קרום. לעומתו, המוליכות תלויה בריכוז התעלות השונות על פני הקרום, בסוג התעלות ובתכונותיהן, ולכן יכולה להשתנות אפילו מאזור לאזור באותו תא. מקובל להניח מוליכות של 10uS לכל מילימטר רבוע של קרום, אך זו יכולה להשתנות עד פי חמישה לכאן או לכאן.

כדי להציג את עקרונות הניתוח, נתייחס לתא פשוט, כדורי וקטן, שבו שינויי פוטנציאל בנקודה כלשהי מתפשטים בחלל התא במהירות רבה ביחס לתהליכים חוצי-קרום. אין זה מונע כמובן מן הפוטנציאל התוך תאי להשתנות עם הזמן בעטיים של תהליכים מטבוליים או עצביים, אך בכל עת ניתן לראות את הפוטנציאל כאחיד בכל חלל התא. לפיכך יכונה תא שכזה 'תא שווה פוטנציאל'. אם נתייחס לתא שקוטרו כ- 20um, יהיה שטחו כ- 0.001m^2 ולפיכך יש להניח: C= 10pF G=1nS

בניגוד לשינויים המתחוללים עם הזמן בחלל התא המבוקר, התווך החוץ תאי דווקא די אחיד וקבוע בהתנהגותו. הוא אינו סגור בחללים נפרדים, וכל נקודה בו מושפעת מפעילותם של תאים רבים, וממוצע ההשפעות הוא די אחיד. נניח לפיכך:

Vout = const

ומתח המברנה יסומן:

Vm = Vin-Vout

הזרם דרך המרכיב ההתנגדותי השרוי במתח שכזה יחושב לפי חוק אוהם: Ig = (Vin - Vout - E )G=(Vm-E)G

ממילא, במצב מנוחה, כשאין זרם נקי החוצה את הקרום, יהיה מתח הקרום:

Vm|rest = E = -70mV

שינויים בכמות המטען במרכיב הקיבולי, Q, יתבטאו כזרם דרך מרכיב זה, לפי:

$\;Qc=(Vin-Vout)C=VmC\rightarrow {\partial Qc \over \partial t}=Ic={\partial Vm \over \partial t}$

ננסה כעת לצפות באמצעות המודל החשמלי את התוצאה שהתקבלה בניסוי הזרקת הזרם שתואר בהקדמת הפרק. המערך הניסויי הוא כזה:

Add caption here

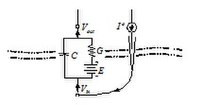
אם נזריק זרם מדוד, I0 , לתוך התא, הזרם ייצא דרך מערכת הנגד-קבל, ויתקיים:

$\;I0=Ig+Ic=(Vm-E)G+{\partial Vm \over \partial t}$

ובניסוח אחר:

$\;{\frac {C}{G}}{\partial Vm \over \partial t}={\frac {I0}{G}}-(Vm-E)$

היינו, השינוי של מתח הקרום בכל עת מתכונתי להפרש בין המתח שמוסיף הזרם I0 על פני הנגד לבין המתח שהיה על פניו רגע לפני כן. קבוע המתכונת מייחס את שינויי המערכת לצעדי הזמן, ומהווה את קבוע הזמן של המערכת כהגדרתו המוכרת:

$\;\iota ={\frac {C}{G}}$

בתא המודגם כאן עם הערכים (1-4) יהיה ערכו של קבוע הזמן כ- 10ms. ניסוח מקובל יותר של המשוואה הדינמית הוא:

$\;\iota {\partial Vm \over \partial t}=-Vm+{\frac {I0}{G}}+E$

זו משוואה מסדר ראשון, שפתרונה כולל חלק הומוגני וחלק פרטי:

$\;Vm(t)=Vm|t=0*e^{(}{\frac {-t}{\iota }})+{\frac {1}{G\iota }}\int \limits _{0}^{t}{e^{\frac {t_{2}-t}{\iota }}}(I0(t_{2})+EG)dt_{2}$

החלק ההומוגני, הראשון, מבטא את המתח ההתחלתי, שאינו תלוי בהתערבות החיצונית, ושדועך עם הזמן ממילא בגלל זליגת זרם. החלק הפרטי, השני, מבטא את המתח המאולץ המתוחזק על ידי הזרם I0 . נפשט: $\;Vm(t)=Vm|t=0*e^{(}{\frac {-t}{\iota }})+{\frac {1}{G\iota }}\int \limits _{0}^{t}{e^{\frac {t_{2}-t}{\iota }}}(I0(t_{2}))dt_{2}+E(1-e^{\frac {-t}{\iota }})=Vm(t)=Vm|t=0(-E)*e^{(}{\frac {-t}{\iota }})+E+{\frac {1}{G\iota }}\int \limits _{0}^{t}{e^{\frac {t_{2}-t}{\iota }}}(I0(t_{2}))dt_{2}$

היינו, השפעת המתח ההתחלתי הכולל את מתח הריכוזים, והשפעת התופעות המתמשכות ובכללן הזרם המאלץ ומתח הריכוזים.

כפי שחילקנו בין מצב התחלתי לבין השפעתו של זרם חיצוני דרך הקרום, כן ניתן לחלק בין השפעתם של זרמים שונים העוברים בקרום. ההשפעה הכוללת היא סכום ההשפעות הפרטיות של כל אחד מן הזרמים. תוצאה זו נובעת מכך שהמערכת ליניארית, והיא מתבטאת בפתרון (1-16) בעובדה שהזרם המאלץ מופיע באינטגרל, שהוא פונקציה ליניארית. כך לדוגמה, ניתן לפתור את המשוואה עבור כל זרם על ידי פירוק פורייה, ופתרון האינטגרל עבור כל מרכיב ומרכיב בנפרד.

מדוע כה חשוב לדעת מה יקרה בתא העצב אם מוזרק לו זרם? ובכן, תחילה מן הראוי לדעת כי מתח המנוחה של הקרום, E, נותר יציב בעינו כי גם הוא תולדה של זרם תמידי המוכנס לתא. כיצד? על ידי 'משאבות יונים' הדוחקות כל העת יוני אשלגן לתא פנימה, תוך שהן מוציאות יוני נתרן החוצה. בדרך כלל נשמר יחס של שלושה יוני אשלגן לכל שני יוני נתרן, ומכאן זרם נקי חיובי קבוע לתוך התא. לפיכך, בתוך הסימן E שבפתרון, מוטמע פתרון פנימי למשוואת זרם המשאבות.

זאת ועוד, קלט סינפטי מתבטא לרוב בכניסת יונים דרך הדנדריטים מחזיקי הסינפסות הפעילות. זרם זה כמוהו כזרם המוזרק על ידי טפיפית, וכן השפעתו, כמתוארת במשוואה (1-14). כעת נראה למה גורם שינוי זה במתח.

מודל סכימה וירי

פעולתו של הנוירון היא, כך מקובל לחשוב, ירי פוטנציאלי פעולה. בעלות המתח בגוף התא עד לסף פתיחת תעלות נתרן תלויות מתח, נפתחות התעלות, יוני נתרן נכנסים ומעלים עוד את המתח, ותהליך ירי פוטנציאל הפעולה מתחיל, וממשיך לאורך האקסון. בעבור פוטנציאל הפעולה כל אחד ואחד מהם, משחררים האתרים הסינפטיים לאורך האקסון מסרנים עצביים הנקלטים בתאי המטרה.

סיר אלאן הודג'קין וסיר אנדרו האכסלי תיארו בפירוט רב את שינויי המוליכות לאורך האקסון במהלך ירי פוטנציאל הפעולה, ובכלל זה התנהגותן של תעלות הנתרן והאשלגן עם השינויים במתח. פרטים אלה, אם יוכנסו למודל החשמלי שתואר עד כה, ייטיבו לתאר את התנהגות תא העצב בעקבות עליית מתח הקרום עד לסף הירי, ואף את השינויים החשמליים בו במהלך הירי עצמו. אלא שלצרכינו אנו, אין התועלת שבכך שווה את סירבול המודל. תחת זאת, נמשיך להשתמש במודל הפשוט שתואר, וכל אימת שהמתח, לפי מודל זה, מגיע לסף ירי, נעצור לרגע את השימוש במודל זה, ונאמר בפשטות שברגע זה מתרחש פוטנציאל פעולה. מיד עם סיומו, נחזור אל המודל הפשוט כמו לא אירע דבר. לפי מודל זה, התא מושפע מן הסובב אותו, וסוכם השפעות אלה עד שהן מביאות אותו לסף ירי. לפיכך מכונה מודל זה 'מודל סכימה וירי'.

לפי מודל סכימה וירי, מסכם הנוירון את השפעות המתח של הקלטים המגיעים מן הדנדריטים, 'יורה' פוטנציאל פעולה אם הסכום עבר סף, ונח למשך תקופה רפרקטורית, וחוזר חלילה. יש לזכור שהמתח מיד לאחר ירי פוטנציאל פעולה חוזר למתח מנוחה, שכן במהלך הירי נפתחות תעלות יונים רבות מאוד, וכל השפעה של מתח ש'נאגר' בתא דועכת מיד. עם תום ירי הפוטנציאל, מתחיל הנוירון לסכם את הקלטים מחדש, וחוזר חלילה.

לדוגמה, נבדוק השפעה של קלט רצוף ואחיד. קלט כגון זה ייתכן בחשיפה של נוירון חושי לגירוי קבוע. במונחי המודל, זרם הכניסה, (I(0 , הוא קבוע. אם זרם זה אינו קיים, מתח התא הוא מתח המנוחה: $\;I(0)=0\rightarrow Vm=E$

אם הזרם חלש, יעלה המתח לרמה המתאימה לפי המודל, וידעך למתח המנוחה עם היפסק הזרם. העלייה והדעיכה הם אקספוננציאליות לפי קבוע הזמן, ועליית המתח שואפת לערך האסימפטוטי: $\;Vmax=E+{\frac {I(0)}{G}}$

(אין צורך לפתור ממש את המשוואה הדינמית. די לאפס בה את גורם ההשתנות בזמן המופיע באגף השמאלי).

Add caption here

עם הגדלת מדרגת הזרם, יעלה גם המתח המכסימלי. מתח הסף הנדרש להתחלת פוטנציאל פעולה יסומן: Vth. כדי שזרם הקלט יוכל לגרום למעבר סף ולירי, הוא חייב להיות גדול מערך הזרם הקריטי לירי:

math>\;I0 > I0f= (Vth- E)G </math>

אחרת, גם לולי העיכוב הקיבולי לא יעבור המתח את הסף.

אם מתח הקרום ההתחלתי הוא מתח המנוחה, אזי, עם כניסת הזרם, ישתנה המתח לפי: $\;Vm(t)=E+{\frac {I0}{G\iota }}\int \limits _{0}^{t}{e^{\frac {t_{2}-t}{\iota }}}dt_{2}=+E+{\frac {I0}{G\iota }}(1-e^{\frac {-t}{\iota }})$

היינו, עלייה אקספוננציאלית ממתח המנוחה לעבר האסימפטוטה. אך המתח לא יגיע לאסימטוטה זו. בהגיעו למתח הסף, יזנק למתח חיובי גבוה הנגרם מכניסת יוני נתרן רבים, וישוב מיד למתח המנוחה. זרם הקלט עדיין קיים, ולכן שוב יעלה המתח אספוננציאלית, ושוב יתרחש פוטנציאל פעולה עם הגיעו למתח הסף, וחוזר חלילה, עד היפסק זרם הקלט. או אז ירד המתח אקספוננציאלית מן הנקודה בה הוא שרוי באותה העת, וידעך חזרה למתח המנוחה.

Add caption here

הזמן העובר עד הגעה למתח סף יחושב לפי:

$\;Vth=Vm(T*)=E+{\frac {I0}{G}}({1-e^{\frac {T*}{\iota }}})$

לפיכך

$\;T*={-\iota }\ln(1-{\frac {(Vth-E)G}{I0}})={-\iota }\ln(1--{\frac {I0f}{I0}})$

היינו, ככל שזרם הקלט גדל ביחס לזרם הקריטי, כך מתקצר הזמן לירי. לפי שיקול זה, נראה שניתן להמשיך ולהגדיל את קצב הירי עם העלאת זרם הקלט, לכאורה עד בלי סוף. אלא, שלאחר כל ירי מושבתות תעלות הנתרן למשך תקופה רפרקטורית, Tr , שערכה הוא כ- 1ms . במהלך תקופה זו לא יכולות התעלות להיפתח, ולכן לא יכול להתפתח פוטנציאל פעולה. לכן, אם הזרם קבוע, זמן המחזור יהיה: T = T* + Tr

וממילא, קצב הירי יהיה: $\;f=T^{-}1={\frac {1}{T*+Tr}})$

לפיכך, גם אם זרם הקלט הוא עצום, עד ש: T* ->0 , קצב הירי מוגבל עד לכ- 1000 פוטנציאלי פעולה בשנייה. התמונה המתקבלת מן המודל היא כזו:

Add caption here

והיא מתאימה לזו המתקבלת בניסוי שתואר בהקדמה לפרק זה.

= פעילות סינפסית

  Normal  0          false  false  false    EN-US  X-NONE  HE                                       MicrosoftInternetExplorer4

פוטנציאל הפעולה שנוירון יורה, משחרר מסרנים עצביים באתרים הסינפטיים הפזורים לאורך שלוחות האקסון. קולטנים בנוירונים בתר סינפטיים קולטים את המסרנים ופותחים, במישרין או בעקיפין, תעלות יונים בקרום הדנדריטים, שדרכן נכנסים יונים לתא הבתר סינפטי. זה זרם קלט לנוירון, ואם יסתכם עם זרמים נוספים משלוחות דנדריטיות נוספות בתא, ויעלה את מתח גוף התא מעבר לסף, הנוירון הבתר סינפטי יירה גם הוא.

פתיחת תעלת קלט גורמת לזרם יונים רגעי דרך קרום התא. אם הוא זרם כניסה של יונים חיוביים, כנתרן או סידן, או שהוא זרם יציאה של יונים שליליים, ככלור, הרי שהמטען החיובי בדנדריט יעלה מעט, ואיתו גם מתח הקרום. עלייה קלה זו של מתח הקרום בדנדריט בתר סינפטי נקראת EPSP – Excitatory Post Synaptic Potential. הזרם היוצר אותה נקרא EPSC. אם הזרם הוא כניסה של יונים שליליים, או יציאה של חיוביים, המטען הדנדריטי ירד מעט, ויעכב את מגמת עליית המתח לעבר סף ירי, אם ישנה כזו. דעיכה רגעית ומעכבת זו תיקרא IPSP – Inhibitory PSP, והזרם היוצר אותה – IPSC.

עירור המתח הבתר סינפטי, או עיכובו, מתקדם לאורך הדנדריט עד גוף התא, אך המטענים העודפים מתפזרים או זולגים דרך הקרום בזמן הזרימה לאורך הדנדריט. לפיכך, אם עוקבים אחר גל המתח מנקודת כניסתו ועד גוף התא מגלים שהוא דועך ברמתו ומתמשך בזמן. גם קלט חזק לתא ידעך עד הגיעו לגוף התא, ולפיכך לא יירה התא, אלא אם חברו יחדיו מספר רב של קלטים סינפטיים על פני העץ הדנדריטי של התא. מטבעו, זרם הקלט זעיר, ולבדו משפיע אך מעט על המתח הקרום בגוף התא. לכן נתייחס אליו כאל זרם קלט במודל סכימה וירי.

כאמור זרם הקלט נגרם מפתיחה רגעית של תעלות. פתיחה שכזו משנה את מוליכות הקרום באתר הסינפטי, Gs , והיונים המסויימים העוברים בתעלות אלה זורמים בהתאם לפער בין מתח הקרום באתר הסינפטי, Vs , לבין מתח המנוחה Es המתאים להפרש הריכוזים של יונים אלה משני עברי הקרום. או: Is = Gs (Vs - Es ) 1

זרם זה עובר בקרום, בנקודה שמרחקה מגוף התא לאורך הדנדריט אינו ידוע, וגם לו היה ידוע, אין אנו יכולים לאמוד את השפעת תלאות הדרך על זרם זה עד שיגיע לגוף התא. ניעזר כאן בעובדה שספר זה יוצא לאור בהוצאה פנימית, כדי לבחור אחת משתי הקלות על חישוב השפעת הקלט הסינפטי.

ההקלה האחת היא להניח שהדנדריט ממילא כה קצר, עד שהאתר הסינפטי יכול להיחשב כשווה-פוטנציאל עם גוף התא, ועל כן: Vs = Vm

סינפסות רבות ומשמעותיות פזורות ממילא על גופי התאים עצמם, ועל כן אין הקלה זו משוללת לגמרי אחיזה במציאות. נציב את הזרם הסינפטי כזרם קלט במשוואה הדינמית (1-14) של מודל התא:

$\;\iota {\frac {\partial Vm}{\partial t}}=-Vm+{\frac {Is+EG}{G}}=-Vm+{\frac {EG+gs(Vm-Es)}{G}}$

  Normal  0          false  false  false    EN-US  X-NONE  HE                                       MicrosoftInternetExplorer4

וננסח בצורה המקובלת: $\;{\frac {\iota }{1-gs/G}}{\frac {\partial Vm}{\partial t}}=-Vm+{\frac {-gsEs+EG}{G}}$

  Normal  0          false  false  false    EN-US  X-NONE  HE                                       MicrosoftInternetExplorer4

בהתאם לקבוע הזמן הכללי של התא, נגדיר גם את קבוע הזמן באתר הסינפטי: $\;{\iota s}=-Vm+{\frac {C}{gs}}$

  Normal  0          false  false  false    EN-US  X-NONE  HE                                       MicrosoftInternetExplorer4

לפיכך, יחס המוליכויות הוא ההופכי של יחס קבועי הזמן, בהיות הקיבול אחיד בכל הקרום:

$\;{\frac {gs}{G}}={\frac {\iota }{\iota s}}$

לפיכך,

$\;{\frac {\iota s\iota }{\iota s-\iota }}{\frac {\partial Vm}{\partial t}}=-Vm-{\frac {\iota }{\iota s}}Es+E$

  Normal  0          false  false  false    EN-US  X-NONE  HE                                       MicrosoftInternetExplorer4

נניח עתה, מתוקף קרבת הסינפסה לתהליכי גוף התא ומתוקף מיידיות השפעתה, כי תעלות הקלט בסינפסה נפתחות בבת אחת לזמן קצר ונסגרות בבת אחת. היינו, המוליכות קבועה במשך זמן הקלט, ואפסית לפניו או לאחריו. לכן גם קבוע הזמן בסינפסה יישאר קבוע במשך הקלט. במקרה כזה, יהיה שינוי המתח במהלך הקלט הסינפטי לפי פתרון המשוואה האחרונה:

$\;Vm(t)=Vm|t=0*e^{\frac {t(\iota s-\iota )}{\iota s\iota }}+({\frac {-\iota }{\iota s}}Es+E)(1-e^{\frac {t(\iota s-\iota )}{\iota s\iota }})$

  Normal  0          false  false  false    EN-US  X-NONE  HE                                       MicrosoftInternetExplorer4

ואילו בתום הקלט הסינפטי יחזור המתח למנוחה לפי פתרון המשוואה:

$\;\iota {\partial Vm \over \partial t}=-Vm+E$

    Normal  0          false  false  false    EN-US  X-NONE  HE                                       MicrosoftInternetExplorer4

ראוי לציין שכדי שהדינמיקה תעלה בקנה אחד עם המציאות, קבוע הזמן הסינפטי צריך להיות גדול מקבוע הזמן הקרומי הרגיל, היינו, מוליכות הסינפסה קטנה בהשוואה לחדירות הקרום הכללית. אחרת, הזרם הסינפטי יקפיץ מיד את המתח ערכים על סיפיים, והמודל אינו תקף עוד. דרישה זו סבירה בהחלט נוכח זעירותה של הסינפסה ביחס לתא כולו. בהתמלא התנאי, ובפרט אם קבוע הזמן הסינפטי קטן מאוד, קצב עליית מתח הקרום בגלל הפעלת סינפסה קטן אך במעט מקצב ההשתנות הרגיל של מתח זה, כגון בירידת המתח חזרה למנוחה עם סגירת התעלות הסינפטיות.

ההקלה האפשרית האחרת, היא לטעון שאמנם הסינפסה רחוקה מגוף התא, ואין אנו יודעים את ההשפעות על הזרם לאורך דרך ארוכה זו, אך יש להניח שאם הופעלה סינפסה s, ובעטיה מגיע לגוף התא זרם רגעי בגודל I*s דרך הדנדריט המתאים, הרי שזרם זה גורר אחריו בדנדריט שובל דעיכה אקספוננציאלית לפי שיעור math>\; \iota *s </math> , המתאים להשפעה הכוללת של הדנדריט, ועל כן פעימות זרם לגוף התא בגלל PSC תהיינה מהצורה: