מתוך ויקיספר, אוסף הספרים והמדריכים החופשי
סימון אסימפטוטי משמש לתיאור התנהגותן של פונקציות שערכיהם הולכים וגדלים. נציג שלושה סימונים.

[עריכה]תהי  פונקציה שואפת לאינסוף.
פונקציה שואפת לאינסוף.
נסמן  אם ורק אם קיימים
אם ורק אם קיימים  -ים לכל
-ים לכל  כך שעבור כל
כך שעבור כל  מתקיים ש-
מתקיים ש- 
כלומר עבור ערכי  הולכים וגדלים שמקבלת
הולכים וגדלים שמקבלת  , היא קטנה יותר מ-
, היא קטנה יותר מ- עד כדי כפל בקבוע.
עד כדי כפל בקבוע.
-
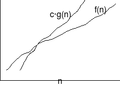
תיאור התמונה
-
קיים

ו-

עבורם

כל זמן ש- <math>
- תהי
 ו-
ו- אז נוכל לומר כי
אז נוכל לומר כי  (הצבה
(הצבה  ) מפני שעבור כל
) מפני שעבור כל  בהכרח מתקיים ש-
בהכרח מתקיים ש- (*)
(*)
- תהי
 ו-
ו- אז נוכל לומר כי
אז נוכל לומר כי  (הצבה
(הצבה  ) מפני שעבור כל
) מפני שעבור כל  בהכרח מתקיים ש-
בהכרח מתקיים ש-
- תהי
 אזי עבור
אזי עבור  נוכל לומר כי
נוכל לומר כי 
- תהי
 אם ורק אם
אם ורק אם  כלומר אם מתקיים ש-
כלומר אם מתקיים ש- מתפקדת כ-
מתפקדת כ- אז נסמן אותה
אז נסמן אותה  .
.
תהי  ו-
ו- אז נוכל לומר כי
אז נוכל לומר כי  (הצבה
(הצבה  ) מפני שעבור כל
) מפני שעבור כל  בהכרח מתקיים ש-
בהכרח מתקיים ש- ולכן
ולכן  (**)
(**)
 אם ורק אם
אם ורק אם  וגם
וגם  כלומר ל-
כלומר ל- יש
יש  , ולאותו הפונקציה,
, ולאותו הפונקציה,  מתקיים שיש
מתקיים שיש  שהוא הפונקציה
שהוא הפונקציה  עצמה,
עצמה,  .
.
- הוכחנו כי אם מתקיים ש-
 ו-
ו- אז
אז (*) וגם מתקיים ש-
(*) וגם מתקיים ש-  (**) ולכן
(**) ולכן  .
.
 (נובע מזהות
(נובע מזהות 
דוגמה להשוואה בין יעילותם של פונקציות
[עריכה]
-
תיאור התמונה
-
תיאור התמונה