אחת התכונות של הוקטור הגאומטרי היא שאין לו מערכת צירים קבועה. בפרק זה אנחנו "נקבע" את מערכת הצירים של הוקטורים ונדון בהצגה של הוקטור בצורה אלגברית ובנוסף נפרט על הפעולות שניתן לעשות בשני וקטורים אלגבריים, חיבור וכפל בסקלר.

רענון[עריכה]

לפני שמתחילים ללמוד את הפרק הזה יש לדעת מעט על ייצוג של נקודות במישור ובמרחב. אם הנושאים האלו כבר מוכרים לך, ניתן לעבור ישירות להצגה האלגברית של וקטור.

מערכת צירים (קואורדינאטות) במישור[עריכה]

במערכת צירים סטנדרטית במישור (המכונה גם מערכת צירים קרטזית או קואורדינאטות קרטזיות) יש לנו שני צירים המאונכים זה לזה הנקראים ציר ה-x וציר ה-y, כאשר ציר ה-x הוא הציר האופקי וציר ה-y הציר האנכי.

נקודת המפגש של שני הצירים נקראת "ראשית הצירים" (או בקיצור ה"ראשית") ובד"כ מסומנת באות $O$ .

נהוג לסמן את ערכי ה-x החיוביים מימין לראשית ואת השליליים משמאל לראשית. כמו כן, ערכי ה-y החיוביים נמצאים מעל לראשית, והשליליים מתחת.

בצורה זו ניתן לרשום במערכת הצירים כל נקודה על המישור (כפי שניתן לראות בבירור בתמונה בצד שמאל).

כאשר רושמים נקודה במישור, נהוג לרשום אותה כזוג סדור כאשר שיעור הx של הנקודה הוא המספר הראשון משמאל ושיעור ה-y הוא המספר השני משמאל. שיעורי ראשית הצירים הם $(0,0)$ .

את המישור ניתן לחלק ל-4 רביעים לפי מערכת הצירים, החלוקה מתחילה מצד ימין למעלה וממשיכה נגד כיוון השעון.

להלן פירוט על הרביעים השונים:

רביע I - הרביע הזה נמצא בצד ימין למעלה. ברביע זה הן ערכי ה-y והן ערכי ה-x הם חיוביים.
רביע II - הרביע הזה נמצא בצד שמאל למעלה, ערכי ה-x שליליים וערכי ה-y חיוביים.
רביע III - נמצא בצד שמאל למטה, ערכי ה-x וה-y הם שליליים.
רביע IV - נמצא בצד ימין למטה, ערכי ה-y שליליים וערכי ה-x חיוביים.

הרביעים השונים במערכת צירים קרטזית במישור

מערכת צירים (קואורדינאטות) במרחב[עריכה]

כמו במישור גם במרחב יש צירים. במרחב, הצירים הסטנדרטיים הם ציר ה-x, ציר ה-y וציר ה-z. כל שלושת הצירים מאונכים זה לזה ורישום של נקודות במרחב דומה מאוד לרישום של נקודות במישור. כדי לתאר נקודות במרחב משתמשים בשלשה סדורה, כאשר שיעור ה-x של הנקודה הוא המספר הראשון משמאל, ולאחריו שיעורי ה-y וה-z.

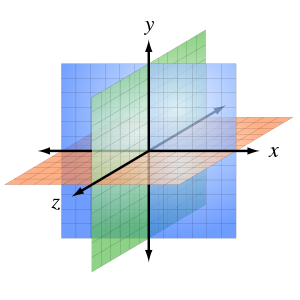
כמו את המישור, גם את המרחב ניתן לחלק למספר חלקים לפי הצירים. עיון באיור משמאל יגלה שמתקבלים 8 חלקים אותם נהוג לכנות תְמנים (ביחיד: תומן; בלועזית: אוקטנט).

בנוסף על כך, נוצרים 3 מישורים שונים המכילים שניים מהצירים. נהוג לסמן את המישורים המסוימים האלה בעזרת סוגריים מרובעים. כך לדוגמה, כדי לסמן את המישור הנוצר מציר ה-x וציר ה-y רושמים כך: [xy].

כל המישורים הנוצרים מהצירים הם:

[xy], [yz], [xz]

המושג של "ממד"[עריכה]

לכל אחד מאיתנו יש מושג של מהו בעצם "ממד". קל להבחין שהמישור הוא דו-ממדי בעוד המרחב הוא תלת-ממדי.

בהמשך, ניתן הסבר מדויק יותר בנוגע למהות של הממד על-ידי הגדרתו בצורה ריגורוזית.

ההצגה האלגברית של וקטור[עריכה]

אנחנו מעוניינים כעת לקחת וקטור כלשהו, "לקבע" אותו למערכת צירים ולתת לו ייצוג בעזרת קואורדינאטות. בשביל זה ניקח וקטור כלשהו ונזיז אותו כך שמוצאו יהיה בראשית הצירים.

נעשה זאת בצורה כזו:

ראשית ניקח וקטור כלשהו ${\rm {\vec {a}}}$ במרחב (במישור הסימונים כמעט זהים, נעמוד על ההבדלים בהמשך) ונזיז אותו כך שמוצאו תהיה בראשית הצירים. כעת, נקודת הסוף של הוקטור נמצאת בנקודה כלשהי במרחב, נסמנה ב-A ונגדיר את הייצוג האלגברי של ${\rm {\vec {a}}}$ להיות שיעורי הנקודה A. (כפי שניתן לראות היטב באיור משמאל).

כעת, ניתן להציג כל וקטור במישור או במרחב כזוג או כשלשה סדורה (בהתאמה).

שימו לב, לוקטורים זהים תהיה הצגה אלגברית זהה!

לדוגמה כללית במישור, ניתן להסתכל על האיור למטה:

מעבר מהצגה גאומטרית של וקטור להצגתו האלגברית[עריכה]

בהינתן שיעוריהן של שתי נקודות במרחב, A ו-B, אנו מעוניינים למצוא את ההצגה האלגברית של הוקטור ${\overrightarrow {\rm {AB}}}$ .

השיטה היא כזו, על-פי החוקים של חיסור שני וקטורים, נוכל לרשום:

${\overrightarrow {\rm {AB}}}={\overrightarrow {\rm {OB}}}-{\overrightarrow {\rm {OA}}}$

כאשר $O$ היא ראשית הצירים.

אבל, אם נסתכל היטב על ההגדרה של הצגה אלגברית של וקטור, נוכל לראות שכדי למצוא את הוקטור ${\overrightarrow {\rm {AB}}}$ מספיק "לחסר" מכל שיעור של B את השיעור המתאים לו ב-A וליצור וקטור חדש, שהוא בעצם, ההצגה האלגברית של הוקטור ${\overrightarrow {\rm {AB}}}$ .

דוגמאות[עריכה]

יהיו הנקודות:

$A=(5,7,-2)B=(1,0,4)$

מצא את הוקטור ${\overrightarrow {\rm {AB}}}$ .

פתרונות[עריכה]

נשתמש בשיטה שהראינו מקודם ונחסר מכל שיעור של B את השיעור המתאים ב-A, ככה שמתקבל:

${\overrightarrow {\rm {AB}}}=(1-5,0-7,4-(-2))=(-4,-7,6)$

השוואה בין שני וקטורים אלגבריים[עריכה]

יהיו ${\rm {\vec {a}}}=(a_{x},a_{y},a_{z})$ ו- ${\rm {\vec {b}}}=(b_{x},b_{y},b_{z})$ שני וקטורים (שימו לב שזוהי הצגה אלגברית שלהם).

אנחנו נאמר שהוקטורים ${\rm {\vec {a}}}$ ו- ${\rm {\vec {b}}}$ שוים זה לזה, אם ורק אם:

$a_{x}=b_{x}$
$a_{y}=b_{y}$
$a_{z}=b_{z}$

כלומר, לוקטורים זהים יש הצגה אלגברית זהה וכל שני וקטורים עם הצגה אלגברית זהה (שיעורי הוקטור שוים זה לזה בהתאמה) הם שוים. כמו כן, ההגדרה נכונה גם במישור.

הערה חשובה! כשנלמד על אורך וזוית של וקטורים בהמשך, נוכל לראות שההגדרה הזו של שוויון בין שני וקטורים מתלכדת עם ההגדרה מהפרק על וקטורים גאומטריים.

חיבור וחיסור של וקטורים אלגבריים[עריכה]

בעזרת הייצוג האלגברי של הוקטורים, ניתן להגדיר חיבור וחיסור בין שני וקטורים אלגבריים כך שההגדרות יתלכדו עם הגדרת החיבור והחיסור של וקטורים גאומטריים.

חיבור וקטורים אלגבריים[עריכה]

באופן כללי, יהיו הוקטורים ${\rm {\vec {a}}}=(a_{x},a_{y},a_{z})$ ו- ${\rm {\vec {b}}}=(b_{x},b_{y},b_{z})$ וקטורים כלשהם במרחב (במישור ההגדרה זהה)

אז וקטור החיבור שלהם ${\rm {\vec {c}}}$ יהיה:

${\begin{matrix}{\vec {c}}&=&{\vec {a}}+{\vec {b}}\\\ &=&(a_{x}+b_{x},a_{y}+b_{y},a_{z}+b_{z})\end{matrix}}$

חיסור של שני וקטורים[עריכה]

גם בחיסור ההגדרה שקולה לזו של וקטורים גאומטריים, הוקטור ${\rm {\vec {c}}}$ יהיה:

${\begin{matrix}{\vec {c}}&=&{\vec {a}}+(-{\vec {b}})\\\ &=&(a_{x}-b_{x},a_{y}-b_{y},a_{z}-b_{z})\end{matrix}}$

כפל של וקטור אלגברי בסקלר[עריכה]

כמו בוקטורים גאומטריים, ניתן להגדיר על וקטורים בהצגה אלגברית כפל בסקלר. צורת הסימון זהה לזו שבפרק על וקטורים גאומטריים.

הגדרה[עריכה]

יהי ${\rm {\vec {a}}}=(a_{x},a_{y},a_{z})$ וקטור ויהי $t$ מספר ממשי כלשהו. נגדיר את הכפל בסקלר כך:

$t{\rm {\vec {a}}}=(t\cdot a_{x},t\cdot a_{y},t\cdot a_{z})$

כלומר, כופלים כל אחת מהקואורדינאטות של הוקטור במספר הממשי.

ההגדרה של הכפל בסקלר בוקטורים אלגבריים מתלכדת עם ההגדרה של כפל בסקלר של וקטורים גאומטריים וכן עם חיבור איטרטיבי של אותו הוקטור מספר פעמים. בנוסף, כל ההערות שניתנו בפרק על כפל בסקלר של וקטור גאומטרי, תקפות גם כאן.