מתמטיקה תיכונית/אלגברה תיכונית/קבוצות ותחומים/הכלה ושוויון
הכלה[עריכה]
כשם שישנו סימון מתמטי שמתאר יחס בין איבר לקבוצה (כלומר יחס השייכות) ישנם סימני יחס נוספים שמסמנים קשר בין קבוצות שלמות. הסימן הבסיסי ביותר לתיאור יחס בין קבוצות הוא סימן ההכלה שמסומן בסימון: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;\subseteq} . נניח למשל שישנן שתי קבוצות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A} ו־הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B} . נניח גם שכל האברים של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A} גם נמצאים ב-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B} כלומר לכל איבר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;x} שמקיים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;x\in A} גם מתקיים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;x\in B} . במקרה זה נאמר ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A} מוכלת ב-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B} ונסמן זאת בסימון:
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle A \subseteq {B}}
הבה נתבונן בדוגמא של הכלה. למשל, נניח שהקבוצה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A} היא קבוצת כל החמוסים. כמו-כן, נניח ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B} היא קבוצת כל היונקים. מכיוון שכל חמוס הוא גם יונק, ברור ש
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle A \subseteq {B}}
כמו-כן, גם ברור מיד שההיפך אינו נכון, שכן בני אדם הם יונקים, אבל הם אינם חמוסים. כלומר, ישנו יונק שאינו חמוס. זאת אומרת ש-
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B\not\subseteq {A}}
|
כדאי לדעת: שימו לב! יחס ההכלה איננו סימטרי! יש לשים לב לכיוון ההכלה. ישנו דמיון בין סימן ההכלה לסימן יחס הסדר (גדול - < או קטן >). הצד הפתוח מצביע לכיוון הקבוצה ה"גדולה" יותר ואילו הצד הסגור לכיוון הקבוצה ה"קטנה" יותר. בדומה לסימן יחס הסדר. |
אם קבוצה מוכלת בקבוצה אחרת אז היא נקראת גם תת-קבוצה של הקבוצה ה"גדולה" יותר. בדוגמא שלנו, קבוצת החמוסים היא תת-קבוצה של קבוצת היונקים, אבל לא תת-קבוצה של קבוצת בני האדם. בני-האדם לעומת זאת הם כן תת-קבוצה של קבוצת היונקים.
הכלה ממש והכלה חלשה[עריכה]
נדבר על ההבדל בין הכלה ממש להכלה חלשה. נדמיין מצב שבו ישנן שתי קבוצות, למשל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A} ו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B} . נניח גם שכל האברים של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A} שייכים גם ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B} . במצב זה, כפי שכבר ראינו
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle A\subseteq {B}}
אבל, כאן יתכן ששתי הקבוצות מכילות בדיוק את אותם האברים. לכן סימן זה נקרא הכלה חלשה. הכלה חזקה או בשמה השני הכלה ממש זה מצב שבו בקבוצה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B} ישנו לפחות אבר אחד שאינו שייך ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A} . מצב זה יסומן כך:
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A\subset {B}}
שוב רואים כאן דמיון לסימון יחס הסדר (גדול-קטן) הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;<} .
שוויון[עריכה]
המצב שוויון בין קבוצות הוא מצב שקל מאוד לדמיין. אם שתי שתי קבוצות מוכלות אחת בתוך השניה (הכלה חלשה לשני הכיוונים) אז הקבוצות תקראנה שוות. כלומר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A\subseteq {B}}
וגם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B\subseteq {A}}
שניהם מתקיימים ביחד.
הבה נתבונן על התכונות הבסיסיות של סימן השוויון. השוויון חייב להיות סימטרי. כלומר לומר ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A=B}
זה אותו דבר כמו להגיד ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B=A}
. זה נכון בגלל שאם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A\subseteq {B}}
וגם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B\subseteq {A}}
אז גם מתקיים ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B\subseteq {A}}
וגם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A\subseteq {B}}
. גם צריך להתקיים שלכל קבוצה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A=A}
. זה נכון כי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A\subseteq {A}}
וזה כמובן נכון לשני הכיוונים.
ישנה עוד תכונה חשובה של שוויון והיא שאם ישנן שלוש קבוצות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B}
, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A}
ו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;C}
וגם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A=B}
ו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B=C}
אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A=C}
(בדוק!).
סימון בדיאגרמות[עריכה]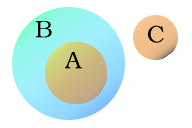
ישנה דרך פשוטה לסמן יחסים בין קבוצות בצורה של ציור או דיאגרמה. לעיתים נקראות דיאגרמות אלו דיאגרמות וֶן, אך למעשה דיאגרמות אלו מיוחסות לכמה מתמטיקאים שונים. למשל, אם ישנה קבוצה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;A}
אשר מוכלת בקבוצה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;B}
וקבוצה נוספת הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \;C}
אשר אין לה בכלל אברים משותפית עם השתיים האחרות, נצייר זאת כעיגול גדול שבתוכו עיגול קטן, כאשר עיגול נוסף מחוץ לשניהם ללא נקודת מגע (ראה דיאגרמת אוילר).
נציג נושא זה שוב בפרק הבא.
הכלה ושוויון של קבוצות מיוחדות[עריכה]
לפי ההגדרה שלהן, נוכל לאמר מספר דברים ברורים לגבי הקבוצות המיוחדות, למשל, קבוצת המספרים הטבעיים-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \mathbb{N}} מוכלת בקבוצת המספרים הממשיים-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \mathbb{R}} וקבוצת המספרים השלמים-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \mathbb{Z}} . כלומר, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \mathbb{N}\subset{\mathbb{Z}}} וגם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \mathbb{N}\subset{\mathbb{R}}} . חשוב לציין שאם מתקיימת הכלה חזקה, אז בפרט מתקיימת גם החלה חלשה. לכן גם מתקיים ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \mathbb{N}\subseteq{\mathbb{Z}}} וגם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \mathbb{N}\subseteq{\mathbb{R}}} . ברור גם ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \mathbb{N}\subset{\mathbb{R}}} וגם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/v1/":): {\displaystyle \mathbb{N}\subset{\mathbb{Z}}} .
| הפרק הקודם: מושגים בסיסיים בתורת הקבוצות |
הכלה ושוויון תרגילים |
הפרק הבא: איחוד וחיתוך |