מתמטיקה תיכונית/אלגברה תיכונית/מספרים מרוכבים/המישור הקרטזי
מראה
המישור הקראטזי
[עריכה]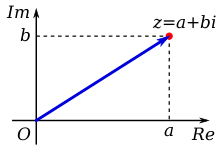
בפרקים הקודמים כבר ראינו כי כל מספר מרוכב () בנוי מחלק ממשי () וחלק מדומה ().
כאשר גם וגם הם מספרים ממשים () כלומר ניתן לחשב על כל מספר מרוכב כעל זוג של מספרים ממשיים. נביא כעת כמה דוגמאות להקבלה זו:
במילים אחרות ניתן להציג את המספר המרוכב בהצגה האלגברית כאשר ציר ה- משמש כציר המספרים הממשים ו- כציר המספרים המספרים המדומים כלומר נייצג את המספר המרוכב כך .
הערך המוחלט
[עריכה]
הערך המוחלט של מספר מרוכב מרחקו של נקודה מראשית הצירים כלומר .
נרחיב: האנך אל ציר ה- במעגל היחידה יוצר משולש ישר זווית שצלעותיו ויתרו, הרדיוס, נסמן כ- .
על פי משפט פיתגורס ועל כן
מהו מרחק?
[עריכה]- מספר ממשי חיובי זאת מכיון שאורך של קו הוא תמיד מספר ממשי וחיובי.
- מרחק בין שתי נקודות יהיה אפס אם ורק כאשר הוא נמדד מנקודה לעצמה - במקרה כזה אין קו בין שתי הנקודות, כי הן נמצאות באותו מקום. ניתן לומר כי קיים קו "מנוון" בין שתי הנקודות, שאורכו אפס.
- נצפה שהמרחק מנקודה לנקודה יהיה זהה למרחק מנקודה לנקודה . זאת מכיון שאורך של קו לא תלוי בשאלה האם אנחנו מותחים אותו מהנקודה הראשונה לשנייה, או מהנקודה השנייה לראשונה.
- אי-שוויון המשולש - המרחק שבין שתי נקודות יהיה קטן או שווה לסכום המרחקים של שתי הנקודות מנקודת ביניים שלישית. משפט זה מבוסס על צלעות במשולש סכום של שתי צלעות גדול מהצלע השלישית. כלומר בהינתן שלושה קדקודים, שתי נקודות - והנקודה . הישר קטן מסכום . לעומת זאת שוויון יתקיים כאשר הנקודה תהיה על הקו שמחבר את ובמקרה זה המשולש שנקבל יהיה בעל שטח אפס.
















