מושג הפונקציה (באנגלית: function) הוא מושג יסודי ומרכזי בחשבון הדיפרנציאלי והאינטגרלי והוא בעל שימושים רבים הן במתמטיקה והן במדע. עיקרו של החשבון הדיפרנציאלי והאינטגרלי עוסק בפונקציות, בתכונותיהן ובבעיות הקשורות אליהן ומסיבה זו חשוב להכיר את הנושאים הקשורים איליהן היטב. מטרתו של פרק זה היא להציג נושאים בסיסיים בפונקציות ותכונותיהן אשר יסייעו לך בהמשך לימוד הספר.

רשימת הפרקים

פונקציות כלליות

סעיף ראשון: פונקציות כלליות - הגדרות ומושגים ראשונים

ידע קודם נדרש

טרם אתה ניגש ללמוד פרק זה עליך לדעת מספר מושגים בסיסיים בתורת הקבוצות. במידה ואין לך היכרות עם הנושא אתה יכול לקרוא את הסעיף מושגים בסיסיים בתורת הקבוצות שבספר אלגברה תיכונית בכדי להשלים את החסר ולאחר מכן לחזור ללימוד הספר. בהצלחה!

דוגמאות

לפני שנפנה להגדרת הפונקציה נביא מספר דוגמאות אשר יסייעו לך לקבל תחושה כללית לגבי מהי פונקציה.

מושג הפונקציה הוא כנראה תולדה של המחקר המדעי - תופעות מדעיות רבות בעלות תלות אחת בשנייה ניתנות לתיאור על ידי פונקציה. כך למשל מהירות הנפילה של גוף תלויה בזמן הנפילה וכמו כן סיכוייו של אדם לחלות במחלת לב תלויים בגילו. אנו אומרים שמהירות הנפילה היא פונקציה של זמן הנפילה ושסיכוי התחלואה הוא פונקציה של גיל האדם. קיימות דוגמאות רבות נוספות לשימוש פונקציות במדע, במיוחד בפיזיקה - כל מי שעוסק בה ודאי מכיר את המושג.

קיימות גם פונקציות מתמטיות. כך למשל, ניתן להגדיר פונקציה המתאימה לכל מספר את המספר הגדול ממנו ב-2 או להגדיר פונקציה המתאימה לכל מספר את ריבועו (המספר כפול עצמו). גם כאן, בדומה לדוגמאות הקודמות, משתנה כלשהו תלוי במשתנה אחר.

דוגמה נוספת לפונקציה היא פונקציה המתאימה לכל אדם את מספר תעודת הזהות שלו. לכל אחד ואחת יש מספר תעודת זהות משלו, מסיבה זו מספר תעודת הזהות תלוי באדם שבחרנו. לכן אומרים שמספר תעודת הזהות הוא פונקציה של האדם לו הוא שייך.

בכל הדוגמאות האלו מתוארת תלות בין משתנה אחד למשתנה השני ואכן, כפי שתראה בהמשך, כל פונקציה מתארת תלות בין שני משתנים כלשהם.

התאמה

נפנה כעת להגדרת הפונקציה אך קודם, בכדי להגדיר את הפונקציה בצורה מתמטית אנו צריכים תחילה להגדיר את מושג ההתאמה.

באיור משמאל מתוארות שתי דיאגרמות המכונות דיאגרמות חיצים. החיצים מתארים התאמה, כך למשל בדיאגרמה א' אנו מתאימים לכל עיר את המדינה שבה היא נמצאת ובדיאגרמה ב' אנו מתאימים לכל אחד משלושת האבות את בת זוגתו. פעולה כזאת היוצרת קשר בין קבוצה אחת לקבוצה שנייה שמה התאמה. התאמה היא פעולה המתאימה לכל איבר בקבוצה ראשונה לפחות איבר אחד בקבוצה שנייה. לדוגמה אנו יכולים להגדיר התאמה המתאימה לכל אדם את הוריו, התאמה המתאימה לכל מספר את המספר הגדול ממנו פי 2 או התאמה המתאימה למספר 7 את המספרים 4.2 ו-0.

לכל אחת מהקבוצות יש שם, הקבוצה הראשונה היא קבוצת התחום (באיור קבוצות התחום הן קבוצות הערים וקבוצת שלושת האבות) והקבוצה השנייה היא קבוצת הטווח (באיור קבוצות הטווח הן קבוצת המדינות והקבוצה המכילה את שרה, רבקה, רחל ולאה).

לפי הגדרות אלו נגדיר את ההתאמה כך:

הגדרה 1.1.1: התאמה

התאמה היא פעולה המתאימה לכל איבר בקבוצת התחום איבר בקבוצת הטווח

במידה וקיים כלל הקובע כיצד מתאימים לכל איבר מהתחום איבר מתאים בטווח הוא מכונה כלל ההתאמה (לעתים גם חוק ההתאמה).

שים לב:

א. בתחום לא יכול להיות איבר שלא מותאם לו איבר בטווח, כלומר לכל איבר בתחום יש איבר מותאם בטווח.

ב. בטווח יכול להיות איבר שאין לו איבר בתחום המותאם אליו.

במידה ומספר האיברים לא גדול מדי או אינסופי נהוג להמחיש התאמות על ידי דיאגרמות חיצים מסוג שמופיע באיור.

א.	ב.	ג.
ד.	ה.	ו.

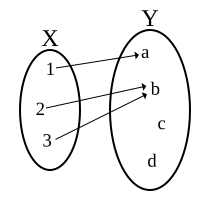בדיאגרמות החיצים המופיעות למעלה מסומנות קבוצות התחום ב-X וקבוצות הטווח ב-‏Y.‏

עכשיו תורכם:

נסה על סמך ההגדרה שניתנה לך לקבוע אילו מבין דיאגרמות החיצים המופיעות למעלה מתארות התאמה

תשובה

כל הדיאגרמות פרט לדיאגרמה ב' מתארות התאמה. ניתן לראות שבדיאגרמה ב' למספר 1 שנמצא בקבוצת התחום לא מותאם איבר בקבוצת הטווח ולכן הדיאגרמה איננה מתארת התאמה

הגדרת הפונקציה

על סמך שני המושגים שהוגדרו קודם נגדיר מהי פונקציה:

הגדרה 2.1.1: פונקציה

פונקציה היא התאמה המתאימה לכל איבר בתחום הפונקציה איבר אחד ויחיד בטווח הפונקציה

שים לב: כל פונקציה היא התאמה אך לא כל התאמה היא פונקציה.

על פי הגדרה זו פונקציה מורכבת משלושה מרכיבים:

א. קבוצת התחום של הפונקציה.

ב. קבוצת הטווח של הפונקציה.

ג. ההתאמה עצמה או כלל ההתאמה.

ההבדל בין התאמה רגילה להתאמה שהיא גם פונקציה הוא שבהתאמה רגילה ניתן להתאים לאיבר אחד בתחום יותר מאיבר אחד בטווח ואילו בהתאמה שהיא גם פונקציה לא ניתן לעשות זאת.

דוגמאות

א. התאמה המתאימה לכל מספר טבעי את ריבועו היא פונקציה.

ב. התאמה המתאימה לכל אדם את צבע עיניו היא פונקציה.

ג. התאמה המתאימה לכל אדם את אזרחותו איננה פונקציה - יש אנשים עם מספר אזרחויות.

ד. התאמה המתאימה לכל מספר את השורש הריבועי שלו איננה פונקציה - למספרים שליליים לא קיים שורש ריבועי.

ה. התאמה המתאימה לכל מספר גדול מ-0 את השורש הריבועי שלו היא כן פונקציה.

ו. התאמה המתאימה לכל עיר את המדינה שבה היא נמצאת היא פונקציה.

ז. התאמה המתאימה לכל אחד מהמספרים 2 ו-0 את המספר 80 היא פונקציה.

ח. התאמה המתאימה לכל מספר את ההופכי שלו איננה פונקציה - לאפס לא קיים הופכי.

ט. התאמה המתאימה לכל מספר פרט ל-0 את ההופכי שלו היא כן פונקציה.

עכשיו תורכם:

נסה על סמך הגדרה זו והדוגמאות שניתנו לך לקבוע איזו מבין ההתאמות המתוארות בדיאגרמות א'-ו' שמופיעות בסעיף הקודם הן פונקציות

תשובה

ההתאמות המתוארות בדיאגרמות א',ג',ה', ו-ו' הן פונקציות

סימון פונקציות

פונקציות כלליות

פונקציות נוהגים לסמן באמצעות אותיות לטיניות (אנגליות) קטנות - לרוב באמצעות האותיות $\ f,g,h$ ובעיקר באמצעות האות f) f היא האות הראשונה במילה האנגלית function שפירושה פונקציה). דרך נוספת לסימון פונקציות היא באמצעות אינדקסים. לאות f (או לכל אות אחרת) אנו מצמידים מספר קטן מתחת לה שיהווה "מספר סדורי" של הפונקציה. לדוגמה אנו יכולים להגדיר את הפונקציות $\ f_{1}$ , $\ f_{2}$ וכו'. בנוסף לכך, קיים סימון הנועד לציין מה תחום הפונקציה ומה טווח הפונקציה. אם אנחנו נסמן את תחום הפונקציה ב-A ואת טווח הפונקציה ב-B נסמן את הפונקציה f כך:

$\!\,f:A\rightarrow B$

לסימון יש לצרף את כלל ההתאמה.

תמונה, מקור ותחום הגדרה

נגדיר מהו מקור ומהי תמונה:

הגדרה 3.1.1: מקור

כל איבר השייך לתחום הפונקציה נקרא מקור

הגדרה 4.1.1: תמונה (של מקור)

איבר בטווח הפונקציה המותאם למקור נקרא התמונה של המקור (או בקיצור תמונה)

כמו כן נגדיר תמונה של קבוצה. נסמן ב-A קבוצה כלשהי החלקית לקבוצת התחום של הפונקציה f. נגדיר את התמונה של A כך:

הגדרה 5.1.1: תמונה (של קבוצה)

קבוצת כל התמונות של האיברים השייכים ל-A תקרא התמונה של A ותסומן $\ f(A)$