מה זה אומר בעצם?/קפלר והכוכבים
צורות תלת מימדיות משוכללות
[עריכה]במאה ה-16 חי בגרמניה מתמטיקאי בשם יוהאנס קפלר, שאהב והתמחה בגאומטריה, ובעיקר בצורות תלת מימדיות. קפלר בין השאר המציא סוגים חדשים של צורות תלת מימדיות שאף אחד לא חשב עליהם קודם. קפלר התחיל בצורות דו מימדיות. אם ניקח מחומש משוכלל, ונצייר את כל האלכסונים שלו, נקבל צורה חדשה שנקראת הפנטגרם, או כוכב המזרח:
-
האלכסונים במחומש יוצרים את כוכב המזרח
מה אם נעשה אותו דבר עם צורות תלת מימדיות? ובכן אלכסון של צורה תלת מימדית הוא לא קו אלא מישור, ואכן בעזרת 'אלכסונים' כאלו ניתן ליצור כל מיני צורות תלת מימדיות מוזרות. לדוגמא אם לוקחים צורה תלת מימדיות בשם דודקהדרון (הציור הימני ביותר למטה, מתוך האלכסונים שלה ניתן לבנות כל מיני צורות מורכבות כגון אלו:
-
הדודקהדרון
-
-
דבר נוסף שריתק את קפלר היה צורות מושלמות. בדו-מימד אנחנו קוראים לצורות מושלמות בשם 'מצולעים משוכללים' ואלו מוגדרים בתור מצולעים שבהם כל הצלעות וכל הזויות שוות. באותו אופן אפשר לחשוב על צורות תלת מימדיות מושלמות. לצורות התלת מימדיות קוראים 'פאונים', מכיוון שהם בנויים מפאות (כל פאה היא מצולע) ופאונים משוכללים הם פאונים שבהם:
- כל הצלעות שוות
- כל הזויות שוות (ומכאן הפאונים מורכבים ממצולעים משוכללים)
- כל הפאות זהות
- אותו מספר פאות נפגש בכל קודקוד
דוגמא אחת מוכרת לפאון משוכלל היא הקובייה, שניתן להגדיר אותה בתור פאון הבנוי מ6 ריבועים, כאשר בכל פינה נפגשים בדיוק 3 מהם. עוד דוגמא שראינו למעלה לפאון משוכלל היא ה'דודקהדרון' שהיא צורה הבנויה מ-12 מחומשים.
כמה סוגים שונים של פאונים משוכללים יש? ההגיון הפשוט אומר שכמו שיש אין סוף סוגים של מצולעים משוכללים (לכל מספר צלעות יש מצולע משוכלל עם אותו מספר צלעות), כך יש אין סוף סוגים של פאונים משוכללים. אלא שהמציאות שונה מאוד מההגיון הפשוט: מסתבר שיש רק 5 פאונים משוכללים ואלו הם:
-
טטרהדר
-
קוביה (קרויה גם הקסהדר)
-
אוקטהדר
-
דודקהדר
-
איקוסהדר
חמשת הפאונים המשוכללים נקראים ה'פאונים האפלטוניים' על שם הפילוסוף היווני הגדול אפלטון, שמזכיר אותם באחד הדיאלוגים שלו. אפלטון התפלא מאוד על כך שקיימים רק 5 פאונים כאלו, וחשב שחייבת להיות לכך משמעות, וכאלפיים שנה לאחר אפלטון, אותה מחשבה בדיוק העסיקה את קפלר. קפלר חשב לעצמו שיש רק 5 פאונים משוכללים, וקיימים בדיוק 5 כוכבי לכת (זה מספר כוכבי הלכת שהיו ידועים בתקופתו), ולכן מוכרח להיות קשר בין שני הדברים.
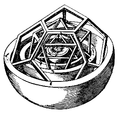
קפלר העמיק בסוגיה והגיע למסקנה שיש קשר עמוק בין הגדלים של חמשת הכוכבים, לבין המרחקים של חמשת הכוכבים מהשמש. הוא פרסם על כך חוברת בשם 'Mysterium Cosmographicum' ('המיסתורין הקוסמי'), ובה תאוריה יפהפיה על הקשר הזה, וכעת נותר לו רק לוודא שהתאוריה הזאת אכן מסתדרת עם המציאות. לשם כך הוא היה צריך גישה לנתונים המדויקים ביותר שהיו בנמצא לגבי כוכבי הלכת. לשם כך הוא הרחיק לכת עד לפראג, לחצר של האסטרונום הגדול ביותר של התקופה, טיכו ברהה. בפראג קפלר עתיד יהיה לפענח לראשונה בתולדות ההיסטוריה את אחת השאלות העתיקות ביותר שהעסיקו את בני האדם: איך לתאר את תנועת הכוכבים בשמיים.
-
הקשר בין הפאונים המשוכללים לכוכבי הלכת
-
(הגדלה של החלק הפנימי של המודל)
טיכו ברהה
[עריכה]
טיכו בראחה היה אחד הדמויות הדגולות, והצבעוניות ביותר באותה התקופה. טיכו היה איש גדל מימדים בעל מראה מרשים ומאיים, שכן אפו נתלש במהלך דו קרב, ובמקום הוא התקין לעצמו אף מברזל. טיכו, כמו מלכי התקופה, החזיק לעצמו חצר ובה אנשים צבעוניים רבים, ובערבים הוא היה עורך משתים ארוכים. מסביב לשולחן באותם המשתים ניתן היה למצוא את הגמד ג'פ, שהיה חצי מפגר ודיבר שטויות אך טיכו האמין שהיה לו כוח ניבואי. לפעמים ניתן היה למצוא מסביב לשולחן אתון, שאותו טיכו חיבב במיוחד, ולימד לשתות יין. טיכו עתיד היה לשלם מחיר כבד על המשתים הללו, שכן על פי כללי הנימוס אסור היה לעזוב את המשתה באמצע, גם לא אם אתה זקוק לשירותים. באחד המשתים טיכו כנראה היה זקוק לשירותים, אך לא עזב את המשתה, ולבסוף בלוטת השתן שלו התפוצצה וכתוצאה מכך הוא הלך לעולמו.

אם כן, מה למתמטיקאי מוכשר, שלא לומר חננה, כמו קפלר, עם טיפוס כמו טיכו בראחה? מסתבר, שבנוסף לכל האישיות הצבעונית שלו טיכו היה גם אסטרונום חרוץ ופדנט. לילה אחר לילה טיכו מיפה בדייקנות את המקומות של כל הכוכבים בשמיים, והמדידות שלו היו המדידות המדויקות והמקיפות ביותר בנמצא. לכן הצירוף של תצפיות מדוקדקות כמו אלו של טיכו, עם דמיון מפותח וכישורים מתמטיים כמו אלו של קפלר, נראה כמבטיח במיוחד. אלא שהקשר בינהם התחיל פחות טוב ממה שאפשר היה לצפות, שכן התגלית הראשונה של קפלר כאשר הוא השווה את התאוריה שלו עם התצפיות של טיכו היתה שהתאוריה לא נכונה. עכשיו הקוראים בטח שואלים את עצמם למה לעזאזל הקדשתי כל-כך הרבה זמן בתאור של פאונים משוכללים, ובתיאור המודל של קפלר, אם בסוף מסתבר שהוא לא נכון?
ובכן כשאני, כילד, קראתי על פיזיקה, היה לי הרושם שכל מה שדרוש על מנת להיות מדען הוא לחשוב על רעיונות מבריקים. כך לדוגמא יום אחד נפל לניוטון תפוח על הראש ופתאום הוא חשב על הרעיון של הכבידה. יום אחד איינשטיין חשב על הרעיון ששום דבר לא יכול לנוע מהר יותר מהאור וכך הוא הגיע לתורת היחסות. אלא שהאמת רחוקה מכך. כדי להיות מדען צריך לחשוב על רעיון מבריק, ללכת ולבדוק האם הוא עובד: האם הוא מתאים למציאות, ורוב הסיכויים שהרעיון לא יתאים למציאות בכלל. ואז חושבים על רעיון מבריק אחר, ובודקים גם אותו, וגם הוא לא מתאים, וממשיכים הלאה: בודקים רעיון אחרי רעיון עד שלבסוף מוצאים רעיון שכן מסתדר עם המציאות. בספרי הלימוד, כמובן, תמיד מספרים רק על הרעיון האחרון שהצליח, לא מספרים על 99 הרעיונות הקודמים שלא הצליחו. אז מה זה בעצם מדען? קודם כל מדען הוא מישהוא שלא מהסס לזרוק לפח רעיון, לא משנה כמה הרעיון מבריק, ברגע שהרעיון לא מתאים למציאות. חוץ מזה מדען הוא אדם שלא מתייאש: גם אחרי 99 כשלונות הוא ממשיך לנסות עד שהוא מגיע לרעיון שכן מצליח.
הדרך של קפלר להבנת מסלולי הכוכבים באמת היתה רצופה מכשולים רבים. המכשול הראשון היה שטיכו, גם לאחר שהוא קיבל את קפלר אליו לחצר לא שש לשתף אותו בתצפיות. הסיבה לכך היתה שטיכו גילה לחרדתו שקפלר האמין בתפיסה הקופרניקאית. עד לאותה תקופה האנושות האמינה שהשמש ושאר הכוכבים נעים מסביב לכדור-הארץ. דור אחד לפני קפלר וטיכו, העלה ניקולאוס קופרניקוס את הרעיון שכדור-הארץ, ושאר כוכבי הלכת מסתובבים סביב השמש, ולא להפך. טיכו התנגד לרעיון הזה והחזיק בגישה שהיתה חצי דרך בין שתי הגישות: כוכבי הלכת מסתובבים סביב השמש, אבל השמש מסתובבת סביב כדור-הארץ. בגלל הסיבה האידאולוגית הזאת טיכו חשש לתת את התצפיות שלו לקפלר, שכן אם קפלר אכן יצליח לפענח את תנועת הכוכבים, הוא גם יביא לקריסת תפיסת העולם שבה כדור-הארץ הוא מרכז היקום. אלא שגם לאחר שטיכו לבסוף נעתר ונתן לקפלר את התצפיות שהוא ערך על התנועה של מאדים, לקפלר עדיין לקח שבע שנים של עבודה קשה, עד שהוא הצליח להבין מה הם אומרים.
לפני שנגיע לפתרון של קפלר, חייבים קודם כל להבין מה בדיוק הבעיה: מה הם כוכבי הלכת - או לפחות מה היה ידוע עליהם בתקופה של קפלר, ולמה התצפיות של טיכו יכלו לפענח את החידה שהאנושות לא הצליחה לפענח ב2000 השנים הקודמות.
כוכבי הלכת
[עריכה]אז מה הם בעצם כוכבים? התשובה הראשונה שפיזיקאי ניסיוני צריך לתת היא שכוכבים הם נקודות של אור שרואים בשמיים. מבין הכוכבים יש שניים שבולטים במיוחד: השמש והירח, שכן הם גדולים ובהירים הרבה יותר. השמש מפזרת כל-כך הרבה אור שכאשר היא נמצאת בשמיים לא ניתן לראות כוכבים אחרים. מעבר לזה כאשר מסתכלים על השמיים נראה שרוב הכוכבים תקועים קפואים במקום - לא זזים. אלא שאם מתאזרים קצת בסבלנות רואים שלא זה המצב. למעשה יש רק כוכב אחד שעומד קבוע במקום, והוא קרוי 'כוכב הצפון' שכן הוא אכן נמצא בצד הצפוני של השמיים. שאר הכוכבים, במשך הלילה, מבצעים תנועה עיגולית מסביבו. זה נכון גם לגבי השמש והירח, אלא שאם מתאזרים בעוד יותר סבלנות רואים שהשמש והירח מבצעים תנועה קצת יותר מסובכת: כיוון שכל יום השמש זורחת במקום קצת אחר. בקיץ השמש זורחת במקום דרומי יותר בשמיים, ולכן כאשר היא מקיפה את כוכב הצפון היא עושה מסלול ארוך יותר, ולכן גם הימים בקיץ ארוכים יותר. בחורף השמש זורחת צפונית יותר, ולכן עושה מסלול קצר יותר, ובהתאם גם הימים בחורף קצרים יותר. רוב הכוכבים האחרים עושים לילה אחר לילה את אותו מסלול בדיוק. כלומר אם נביט באותה שעה בדיוק על אותו מקום בדיוק בשמיים, נמצא שם את אותם כוכבים. היוצאים מהכלל הזה (חוץ מהשמש והירח) נקראים כוכבי הלכת.
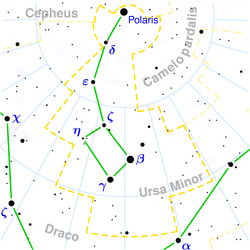
כוכבי הלכת ממבט ראשון לא נראים שונים בהרבה משאר הכוכבים. הם קצת יותר בהירים, אבל לא בהרבה. אלא שאם עוקבים יום אחר יום אחרי התנועה שלהם מקבלים תנועה מבולבלת מאוד: מאדים לדוגמא נראה שלפעמים הוא נע לכיוון אחד, ופתאום מתחרט מבצע פניית פרסה ומתחיל ללכת לכיוון השני. איך אפשר להסביר תנועה מסובכת כזאת?
לאורך השנים אסטרונומים שונים העלו תאוריות שונות לתיאור התנועה הזאת (המוצלחות יותר בתאוריות האלו נקראו ה'אפיציקלות'), וככל שהצטברו תצפיות טובות יותר על תנועת הכוכבים, כך התאוריות השונות נמצאו כולם שגויות. מה עושים מדענים כאשר התאוריות שלהם שגויות? מנסים לתקן אותם: לשכלל אותם. וכך לאורך השנים נוספו תיקונים על-גבי תיקונים שהפכו את תמונת היקום למסובכת יותר ויותר. אז במאה ה-16 עלה ניקולאס קופרניקוס על רעיון פשוט להסבר תנועת הכוכבים: הרעיון שלו היה שאנחנו, חיים על פני כוכב, דומה מאוד לכוכבי הלכת האחרים, ואנחנו, כמו שאר כוכבי הלכת מקיפים את השמש. כתוצאה מכך התנועה של מאדים נראית לנו מסובכת מאוד, כיוון שהיא מורכבת מסך של הסיבוב שלנו סביב השמש, והסיבוב של מאדים סביב השמש. לרעיון של קופרניקוס היה יתרון אחד מרכזי על פני התאוריות הקודמות והוא הפשטות, וזו הסיבה שקפלר תמך בתאוריה הזו. לסיבה הזאת קוראים היום בשם 'תערו של אוקאם': והיא אומרת שכאשר יש כמה תאוריות שכולם תואמות את המציאות באותה מידה, אזי יש לבחור בתאוריה הפשוטה ביותר. במילים אחרות: לא צריך לסבך את מה שלא צריך לסבך.
אלא שלתאוריה של קופרניקוס היו שתי חסרונות מרכזיים: הראשון היא שהיא נגדה את תפישת הכנסייה באותה התקופה. נכון שבתנ"ך לא כתוב במפורש שהשמש מקיפה את כדור-הארץ אבל זה משתמש מהציטוט של יהושוע: "שמש בגבעון דום, וירח בעמק איילון". מעבר לכך אנחנו אוהבים לחשוב שאנחנו מרכז הבריאה ומרכז העולם. בכל תרבות ותרבות בעולם האמינה שעיר הבירה שלה היא מרכז העולם, ורובם המשיכו להאמין בתפיסה הזאת גם שהסתבר שאנחנו חיים על פני כדור, ולכן אי אפשר לראות אף נקודה על המעטפת שלו כמיוחדת יותר מהאחרות. אבל קופרניקוס ביד גסה הרחיק ממנו את מרכז היקום, ושם אותו רחוק מאוד מאיתנו - על השמש. בהמשך התפתחות המדע התפישה בקשר למרכזיות שלנו תספוג סדרה של מכות נוספות: יתברר שגם השמש שלנו היא רק אחת מיני שמשות רבים בגלקסיה שלנו, ולא נמצאת אפילו קרוב למרכז הגלקסיה, וגם הגלקסיה שלנו היא רק אחת מהמון גלקסיות שרואים בשמיים.
הבעיה השנייה עם התורה של קופרניקוס היא שגם, כמו התורות הקודמות, עדיין לא תאמה במדויק את התצפיות, ומכאן שגם היא עדיין לא נכונה.
אם כך כשקפלר ניגש להבין את תנועת הכוכבים הוא הצטייד ברעיונות של קופרניקוס, ובתצפיות לגבי המיקום כוכבי הלכת בשמיים לאורך הזמן. אלא שטיכו ברהה סיפק לו עוד פריט מידע חשוב - המרחק של כוכבי הלכת מכדור-הארץ, וכיצד המרחק הזה משתנה לאורך הזמן.
מדידת המרחק לכוכבים
[עריכה]
הדרך הפשוטה ביותר למדוד מרחקים היא בעזרת סרגל, אבל לרוע המזל לכל סרגל יש את המוגבלויות שלו. לדוגמא הסרגלים הרגילים שאותם ניתן לקנות בחנויות כלי כתיבה הם לרוב באורך של בערך 20 ס"מ והמרחק בין השנתות בהם הוא 1 מ"מ. לכן הם לא מספיק טובים אם רוצים למדוד מרחקים שיותר קטנים ממילימטר, או מרחקים שבהרבה יותר גדולים מ-20 ס"מ. לכן אי אפשר להשתמש בהם בשביל למדוד את המרחק לירח שנמצא במרחק של יותר מ380 אלף קילומטרים מאיתנו, שלא לדבר על למדוד את המרחק למאדים. אם כך איך הצליח טיכו ברהה ואנשים אחרים בני תקופתו למדוד מרחקים עצומים שכאלה?
השיטה שבה טיכו ואחרים השתמשו נקראת שיטת ההיסט (parlax). השיטה מבוססת על אחד המשפטים הראשונים שאנחנו לומדים בבי"ס על גאומטריה, שנקרא משפט ז.צ.ז: "שני משולשים שלהם שני זויות שוות וגם הצלע שבינהן שווה, חופפים אחד לשני." מה זה אומר בעצם? זה אומר שאם אנחנו יכולים למדוד את הזויות אל כוכב נתון משתי נקודות מבט שונות, ואנחנו יודעים את המרחק בין שתי נקודות המבט, אז המשולש שנוצר בין שתי נקודות המבט והכוכב מוגדר היטב, ולכן גם המרחק מוגדר היטב. מה זה אומר שהמרחק מוגדר היטב? זה אומר שאפשר לחשב אותו, ובדיוק בשביל זה (טוב, לא רק בשביל זה) פיתחו מדענים ערביים במהלך ימי הביניים ענף במתמטיקה שנקרא 'טריגונומטריה'.
הטריגונומטריה מתחילה בכך שמסתכלים על משולש ישר זוית (משולש שבו אחת הזויות בת 90 מעלות, הצלעות הסמוכות לה נקראים הניצבים והצלע מולה נקראת היתר) ומגדירים שתי פונקציות הקרויות סינוס וקוסינוס בתור היחס בין אורכי הניצבים לבין היתר (את ההגדרה המדויקת אפשר לראות באיור). ולכן אם אנחנו מסובבים את המבט כך שהזוית בין הכוכב לאחת העיניים שלנו הוא אזי מתוך היפוך של פונקציית הקוסינוס ניתן לקבל את המרחק אל הכוכב.
אם ככה ע"י מדידה של זויות אנחנו יכולים למעשה לפרוס סרגל אל השמיים, ולמדוד את המרחקים אל הכוכבים. השאלה היחידה היא כמה טוב הסרגל הזה? עד איזה מרחקים הוא יכול למדוד? השאלה היא אחת השאלות המרכזיות שבהם עוסקים פיסקאים ניסיונאיים - כל אחד ואחד מכלי המדידה שלנו הוא טוב לדברים מסוימים ולא טוב לדברים אחרים, וחייבים לדעת בדיוק את הגבולות שלו. שיטת ההיסט נשמעת בתאוריה כשיטה שיכולה למדוד בלי בעיה כל מרחק שנרצה, אבל במציאות יש לה הגבלה - וההגבלה היא היכולת שלנו למדוד זויות בצורה מדויקת. כך לדוגמא במדי הזוית שאותם אפשר לקנות בחנות מכשירי כתיבה, המרחק בין שתי שנתות הוא מרחק של מעלה - כלומר אנחנו לא יכולים להשתמש בהם למדוד מרחקים של פחות ממעלה. לטיכו היו מכשירים קצת יותר טובים, אבל לא בהרבה. אז הנה מקום שמי שיודע קצת מתמטיקה, כדאי שינסה לענות על החידות האלו בלבד:
- נגיד שהעיניים שלנו יכולות למדוד זויות בדיוק של מעלה, והמרחק בין העיניים שלנו הוא 6 ס"מ מה המרחק הכי גדול שאנחנו יכולים למדוד בעזרת העיניים שלנו?
- כדי למדוד את המרחק לירח, כאשר שוב אפשר למדוד זויות עד כדי דיוק של מעלה, מה צריך להיות המרחק בין שתי נקודות המבט?
אם ככה בשיטת ההיסט ניתן למדוד מרחקים גדולים מאוד, אפילו את המרחקים אל כוכבי הלכת הרחוקים ביותר במערכת השמש שלנו, וטיכו ברהה ניהל תצפיות שיטתיות ומדויקות בשיטה הזאת - והמידע הזה נתן לקפלר את הבסיס להבנת תנועת הכוכבים. למרבה הצער את המרחק לכל הכוכבים שאינם כוכבי לכת, כוכבים שנמצאים מחוץ למערכת השמש, לא ניתן למדוד בשיטה הזאת ע"י שתי תצפיות על פני כדור הארץ, וזה מכיוון שהמרחקים אל הכוכבים האחרים פשוט גדולים מידי. אבל בשנת __ הגיעו אסטרונומים לרעיון שאנחנו יכולים להאריך קצת את הסרגל שלנו אם נתאזר קצת בסבלנות. הרעיון הוא להשתמש בעובדה שכדור-הארץ סובב את השמש ולכן אם נבצע מדידה פעם אחת בחורף ופעם אחת בקיץ, אזי זה המרחק בין שתי נקודות המבט שלנו הוא פעמיים המרחק שבין כדור-הארץ לשמש, וזה מרחק לא מבוטל בכלל (__ ק"מ). בשיטה הזאת אפשר למדוד את המרחק בינינו לכמה מהכוכבים היותר קרובים אלינו כמו __.
חוקי קפלר
[עריכה]רבים חושבים שעשיית הפיסיקה מצטמצמת לשני תחומים: ביצוע ניסויים והמצאה של תאוריות. אלא שבין שני הדברים החשובים הללו יש עוד שלב שלוקח לא פחות זמן, מקוריות ומאמץ, שלב שקוראים לו עיבוד נתונים. קפלר קיבל לבסוף מטיכו ברהה את הנתונים על המיקום של מאדים בשמיים ועל המרחק אל מאדים, ובתחילה הנתונים הללו כנראה נראו לו כנראה בדיוק כמו שהם ניראו לכל אחד אחר: אוסף של מספרים, ועכשיו היה צריך למצוא בהם איזשהוא סדר והגיון. עיבוד הנתונים הזה דומה מאוד לחידות שנותנים לילדים בבית ספר של 'מצא את המספר הבא בסידרה: 1,1,2,3,5,8,13... כדי לפתור את החידה צריך קודם להבין מה החוקיות שייצרה את הסידרה. במקרה הזה צריך לראות שכל מספר הוא הסכום של שני המספרים הקודמים לו בסידרה (סידרה כזאת נקראת סדרת פיבונאצ'י) ולכן המספר הבא בסידרה הוא 21. הבעיה שעמדה בפני קפלר במובנים רבים היתה דומה, רק קצת הרבה יותר קשה.
את סוף הסיפור כבר סיפרנו: קפלר הצליח למצוא הגיון בנתונים שלו, את ההגיון הזה הוא הצליח לסכם ב-3 חוקים, שקרויים היום על שמו, חוקי קפלר:

החוק הראשון - כוכבים נעים באליפסות
[עריכה]התגלית המרכזית של קפלר היתה שהכוכבים לא נעים סביב השמש בעיגולים אלא באליפסות. אליפסה היא צורה שמתקבלת אם לוקחים עיגול ומותחים אותו בכיוון אחד. דרך אחרת ליצור אליפסה היא לקחת חרוט ולחתוך אותו בזוית, כמו שרואים באיור. למעשה תלוי בזוית שבה חותכים את החרוט ניתן לקבל גם עיגול, וגם עוד שני סוגים של צורות הנקראות פרבולה והיפרבולה (שעל כולם נדבר בהמשך) ומהסיבה הזאת קוראים לצורות הללו חתכים קוניים.
להבדיל מעיגול שלו מרכז אחד, עבור אליפסה יש שתי נקודות אמצע שנקראות שני נקודות המוקד שלה. מה שמיוחד בנקודות הללו הוא שסכום המרחקים מכל נקודה אל שתי הנקודות הללו נשאר קבוע. זה נותן לנו דרך פשוטה לצייר אליפסה: ניקח פיסת עץ, ננעץ בה שני מסמרים וניקח ל

החוק השני - שטחים שווים בזמנים שווים
[עריכה]התגלית המשמעותית השנייה שגילה קפלר היא שהמהירות של הכוכבים במהלך המסלול שלהם מסביב לשמש היא לא קבועה. קפלר גילה שככל שהכוכבים קרובים יותר לשמש כך המהירות שלהם גדלה, וככל שהם רחוקים יותר כך המהירות קטנה. כמה היא גדלה? כמה היא קטנה? ובכן הוא מצא חוק פשוט שעונה על השאלות האלו: דמיינו שאנחנו מותחים קו בין כדור-הארץ לשמש, ומסתכלים על השטח שהקו הזה מכסה כאשר כדור-הארץ נע. קפלר גילה שבזמנים שווים הקו הזה מכסה שטחים שווים. לכן כאשר כדור-הארץ רחוק מהשמש, הקו ארוך ולכן גם עם כדור-הארץ נע לאט הוא עדיין מכסה שטח גדול. לעומת זאת כאשר כדור-הארץ קרוב לשמש הקו קצר יותר ולכן על מנת לכסות שטח שווה כדור הארץ צריך לנוע הרבה יותר מהר.
החוק השלישי - קשר בין זמני המחזור למרחקים
[עריכה]החוק השלישי שמצא קפלר קושר את זמני המחזור של הכוכבים עם המרחק בינהם לבין השמש- והוא אומר שככל שכוכב רחוק יותר כך הזמן שלוקח לו להקיף את השמש ארוך יותר, במילים אחרות שנה על פני מאדים האורך שלה הוא (___) יותר קטן משנה על פני כדור הארץ (365 ימים) מכיוון שמאדים קרוב יותר לשמש. בכמה יותר קצר? ובכן הכלל שמצא קפלר הוא שהזמן בריבוע הולך כמו החזקה השלישית של המרחק.
חשיבות חוקי קפלר
[עריכה]החשיבות הראשונה של החוקים היא בסיפוק יצר הסקרנות שלנו - מאז תקופת האדם הקדמון תמיד בני אדם הסתכלו בשמיים ותמיד כוכבים עניינו אותם. קפלר סוף סוף הצליח להבין את תעלומת תנועת הכוכבים, וזה בפני עצמו הישג גדול. להשג הזה יש גם כמה שימושים לדוגמא בעזרת חוקי קפלר אפשר לנבא במדויק מתי יהיה ליקוי ירח, וליקוי חמה, וגם אנחנו יכולים להישמר ולוודא שאף כוכב לכת או אסטרואיד לא יתנגש בנו בטעות (כמו בעלילת הסרט 'ארמגדון').
אחד הדברים המענינים היא שאותה תנועה שמבצע כדור-הארץ סביב השמש אפשר למצוא בכל מיני מקומות אחרים: לדוגמא באטומים האלקטרון נע מסביב לגרעין באותו אופן (למרות שדברים שם קצת יותר מסובכים בגלל תורת הקוונטים), וגם התנועה של השמש שלנו מסביב למרכז הגלקסיה, גם היא מתנהגת בדיוק לפי חוקי קפלר. בשנת ___ הצליחו חוקרים לראשונה להציץ לתוך מרכז הגלקסיה, ולהסתכל איך כוכבים, כמו השמש שלנו, נעים במהירויות אדירות סביב מרכז הגלקסיה. התמונות שהם קיבלו שכל כוכב נע בתנועה אליפטית, ובדיוק כמו כדור-הארץ ככל שהכוכבים קרובים יותר למרכז הגלקסיה כך הם נעו מהר יותר, וככל שהם התרחקו כך הם נעו לאט יותר. ההבדל העיקרי אם התצפיות על כוכבים היה שאת התפקיד של השמש ממלא בגלקסיה שלנו חור שחור מאסיבי מאוד, שאותו אי אפשר לראות בתצפיות - מכיוון שחור שחור לא פולט שום קרינה. למעשה התצפיות על תנועת הכוכבים סביב החור השחור היוו עדות תצפיתית ראשונה לקיומם של חורים שחורים.
אולם החשיבות הגדולה ביותר של חוקי קפלר היתה בשאלות שהם עוררו. כך קורה תמיד בפיסיקה: כל פתרון הוא שאלה חדשה. בזכות קפלר אנחנו יודעים איך כוכבים נעים, ועכשיו מתעוררת השאלה: "למה?", למה הכוכבים נעים דווקא לפי החוקים המוזרים האלו? את התשובה לשאלה הזאת נתן פיסיקאי בשם אייזק ניוטון, שחי דור אחד לאחר קפלר, והתשובה שלו הסבירה לא רק איך הכוכבים נעים, אלא להסביר באופן כללי איך דברים נעים- ויצר בכך ענף בפיסיקה בשם מכניקה. על כך נדבר בפרק הבא.
קריאה נוספת
[עריכה]- מילדות לבגרות בשביל החלב