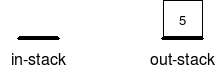מבני נתונים ואלגוריתמים - מחברת קורס/מבני נתונים/תורים/תרגילים/מימוש תור בעזרת שתי מחסניות/תשובה
הרעיון הכללי
[עריכה]נממש את התור כך שיכיל שתי מחסניות:
in-stackתשמש אותנו להכנסת איברים.out-stackתשמש אותנו להוצאת איברים.
כאשר דוחפים איבר v (לתור), פשוט דוחפים אותו למחסנית in-stack שבתור.
בפעולת Dequeue, ננסה לבדוק האם אפשר לשלוף מout-stack. אם כן - סיימנו, אם לא, ראשית נעביר את כל האיבר מin-stack לout-stack, ואז נשלוף מתוכו.

|
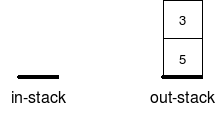
עכשיו תורכם: כיצד ייראה התור אם נדחוף אליו את 11? |

|
עכשיו תורכם: כעת, כיצד ייראה התור אם נשלוף איבר? |
היות שout-stack אינו ריק, פשוט נשלוף את האיבר הראשון מתוכו (כלומר 5):
פסוודו-קוד
[עריכה]להלן מבנה התור (במימוש זה). הוא פשוט מכיל שתי מחסניות.
# A queue (implemented usin-stackg two stacks)
Queue
1 in-stack # A stack to which to Push elements.
2 out-stack # A stack from which to Dequeue elements.
כאשר דוחפים איבר v (לתור), פשוט דוחפים אותו למחסנית in-stack שבתור:
Enqueue(q, v)
1 Push(q.in-stack, v)
בפעולת Dequeue, ננסה לבדוק האם אפשר לשלוף מout-stack. אם כן - סיימנו, אם לא, ראשית נעביר את כל האיבר מin-stack לout-stack, ואז נשלוף מתוכו:
Dequeue(q)
1 if Size(q.out-stack) == 0
2 while Size(q.in-stack) > 0
3 v = Pop(q.in-stack)
4 Push(q.out-stack, v)
5 return Pop(q.out-stack)
קל לממש פעולות אחרות. לדוגמה, אם נניח שהמחסניות תומכות בפעולה Size (המחזירה את מספר האיברים), ורוצים לממש את פעולת Size לתור, פשוט נחזיר את סכום הגדלים:
Size(q)
1 return Size(q.in-stack) + Size(q.out-stack)
לחלופין, אם נניח שהמחסניות תומכות בפעולה Empty (המחזירה האם המחסנית ריקה), ורוצים לממש את פעולת Empty לתור, פשוט נחזיר האם כל אחת מהמחסניות ריקה:
Empty(q)
1 return Empty(q.in-stack) and Empty(q.out-stack)

|
עכשיו תורכם: כיצד תממש את פעולת Front, המחזירה את האיבר הראשון המועמד להוצאה (אך אינה משנה את תוכן התור)? |
נממש זאת באופן דומה לזה שבDequeue של התור, אך נשתמש בTop של מחסנית, כך:
Front(q)
1 if Size(q.out-stack) == 0
2 while Size(q.in-stack) > 0
3 v = Dequeue(q.in-stack)
4 Push(q.out-stack, v)
5 return Top(q.out-stack)
הוכחת נכונות
[עריכה]|
משפט: נניח שב אז (לפי סדר זה, משמאל לימין), הם בדיוק האיברים האחרונים שהוכנסו לתור וטרם הוצאו (כלומר הוא האיבר המוקדם ביותר שהוכנס וטרם נשלף, ו הוא האיבר המאוחר ביותר שהוכנס וטרם נשלף). |
להלן טענת המשפט באופן גרפי:

הוכחה: נוכיח את הטענה באינדוקציה על מספר הפעולות.
(בסיס האינדוקציה) לפני הפעולה הראשונה, 0 איברים הוכנסו או נשלפו, ושתי המחסניות ריקות. הטענה נכונה באופן טריביאלי.
(מעבר האינדוקציה) נניח שהטענה נכונה לאחר מספר פעולות: כעת בin-stack יושבים , בout-stack יושבים , והטענה מתקיימת עד כה. נראה שהטענה מתקיימת לאחר הפעולה הבאה:
- אם הפעולה הבאה היא
Size(אוEmpty) אוTop, שום דבר אינו משתנה, והטענה בוודאי נכונה. - אם הפעולה הבאה היא
Pushשל איברu, אזout-stackלא ישתנה, ותוכןin-stackיהפוך להיות . ואכן, לפי הנחת האינדוקציה, (לפי סדר זה, משמאל לימין), הם בדיוק האיברים האחרונים שהוכנסו לתור וטרם הוצאו. תוכל לראות זאת בתרשים בהמשך. - אם הפעולה הבאה היא
Top, יש שתי אפשרויות:- אם
out-stackאינה ריקה, אז שום דבר אינו משתנה, והטענה בוודאי נכונה. - אם
in-stackריקה, אז לאחר 2-4 בFront, in-stackתהיה ריקה, וout-stackתכיל את האיברים (כלומר האיבר הבא שיישלף). ואכן, לפי הנחת האינדוקציה בדיוק האיברים האחרונים שהוכנסו וטרם הוצאו. תוכל לראות זאת בתרשים בהמשך.
- אם
- אם הפעולה הבאה היא
Dequeue, הטענה דומה מאד לטענה בDequeue.
להלן תיאור גרפי של המצב בPush:

להלן תיאור גרפי של המצב בTop בו out-stack ריק בתחילה:

ניתוח סיבוכיות
[עריכה]|
משפט: הסיבוכיות של פעולות הנה . |
הוכחה: מהתבוננות בפונקציות, קל לראות את הדברים הבאים:
- כל אחת מפעולות התור, למעט
Dequeue(וTop), הנה . Dequeue(או לחלופיןTop) הנה , כאשר הוא מספר הפעולות במחסניתin-stackבעת הקריאה.
אפשר לראות זאת מכך שהלולאה היחידה היא 1-3 בDequeue (או לחלופין Top), וכל אחת מפעולות הרשימה המקושרת היא .
אם מבצעים פעולות, הרי שבכל קריאה לDequeue יהיו לכל היותר איברים במחסנית. מכאן נקבל שזמן הריצה חסום מלמעלה על ידי
.
אם כי המשפט הקודם נכון, נוכל לטעון טענה חזקה יותר.
|
משפט: הסיבוכיות של פעולות הנה . |

|
עכשיו תורכם: וודא שהנך מבין מדוע שני המשפטים אינם סותרים זה את זה. |
ראשית, קל לראות כי הסיבוכיות הנה , משום שאנו מבצעים קריאות לפונקציות, וכל אחת מהן הרי . כל שנותר, לכן, הוא להוכיח חסם . להלן שתי הוכחות לכך.
כדאי לדעת: כל אחת מההוכחות הבאות מסתמכת על צורת ניתוח הידועה בשם amortized analysis. בספר הקורס, הפרק "Amortized Analysis" עוסק בכך. |
להלן ההוכחה הראשונה.
הוכחה: נוכיח את הטענה באינדוקציה על אורך סדרת הפעולות, .
(בסיס האינדוקציה) עבור עלינו להוכיח שסדרת הפעולות (שהיא פעולה יחידה במקרה זה) הנה . ואכן, כשעוברים על הקוד של כל אחת מהפונקציות, ברור שכשהיא הפעולה הראשונה (והיחידה) בסדרת פעולות המתחילה בתור ריק - זמנה הוא .
(מעבר האינדוקציה) נניח שהטענה נכונה לכל קטן (ממש) מ, ונראה שהיא נכונה ל. כפי שהזכרנו, ברור מהתבוננות בקוד שרק לפעולות Dequeue וFront תתכן סיבוכיות שאיננה (וגם זאת בהתאם למצב המחסניות) - לכל אחת מהפעולות האחרות בוודאות סיבוכיות .
אם בסדרת הפעולות לא נקראה אף אחת משתי פעולות אלו, ברור שהסיבוכיות היא . אחרת, נגדיר כ את מספר הפעולה האחרונה בסדרת הפעולות שהיתה מסוג Dequeue או Front (כל אחת מהפעולות אחריהן יכולה להיות, נניח, Enqueue, אך לא אחת משתי אלו). סיבוכיות סדרת הפעולות מ1 עד (כולל) היא , וזאת מהנחת האינדוקציה. סיבוכיות שאר הפעולות היא . סך הכל, לכן, נקבל .
ולהלן הוכחה חלופית.
הוכחה: כדי לראות שסך הפעולות הן , נשים לב לעובדה הבאה. כל ערך v יכול לעבור לכל היותר פעם אחת את המסלול הבא:
Push(q.in-stack, v)(בקריאה לPushשל התור).Dequeue(q.in-stack)(בקריאה לDequeueשל התור).Push(q.out-stack, v)(בקריאה לDequeueשל התור).
לכן כל איבר שנדחף לתור יכול לתרום לכל היותר לסיבוכיות רצף הפעולות. ברור שברצף של פעולות, יידחפו לתור לכל היותר איברים.