מבני נתונים ואלגוריתמים - מחברת קורס/אלגוריתמים/תכנון דינאמי/תרגילים/חיתוך בד/תשובה

המבנה הרקורסיבי[עריכה]

נגדיר כ $\displaystyle m(i,j)$ את מקסימום הרווח מפיסת בד במידות $\displaystyle (i,j)$ .‏

משפט:

$\displaystyle m(i,j)$ נתונה על ידי נוסחת הנסיגה הבאה:

$\displaystyle m(i,j)=\max\{$
$\displaystyle \max _{1\leq i'<i}m(i',j)+m(i-i',j),$
$\displaystyle \max _{1\leq j'<j}m(i,j')+m(i,j'-j),$
$\displaystyle value(i,j)\}$
(כאשר $\displaystyle value(i,j)$ הוא הערך המוחזר מהפונקציה Value(i, j)).

כדאי לדעת:

שים לב שהנוסחה הנ"ל כוללת בתוכה תנאי עצירה, מפני שעבור

\displaystyle i=j=1

, מה שכתוב כאן הינו פשוט

\displaystyle value(i,j)\}

.

אפשר גם לכתוב את נוסחת הנסיגה בדרכים אחרות, ובחלקן גם יופיעו תנאי עצירה בצורה מפורשת יותר.

הוכחה: יש שלוש אפשרויות:

כדאי לחתוך את פיסת הבד אפקית באיזשהו $\displaystyle i'$ (כמתואר בתרשים הבא). נשים לב שאפשרות זו רלוונטית רק עבור עבור $\displaystyle i>1$ .
כדאי לחתוך את פיסת הבד אנכית באיזשהו $\displaystyle j'$ (כמתואר בתרשים הבא אחריו). נשים לב שאפשרות זו רלוונטית רק עבור עבור $\displaystyle j>1$ .
כלל לא משתלם לחתוך את פיסת הבד.

בתרשים הבא, לדוגמה, חיתוך אופקי של הצורה בA בשורה $\displaystyle i'$ ייצור שתי צורות מלבניות בB; לראשונה שבהן יהיו $\displaystyle i'$ שורות:

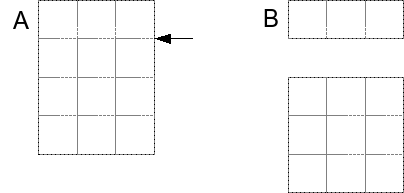
בתרשים הבא, לדוגמה, חיתוך אנכי של הצורה בA בעמודה $\displaystyle j'$ ייצור שתי צורות מלבניות בB; לראשונה שבהן יהיו $\displaystyle j'$ עמודות:

כעת נדון בכל אחת משלוש האפשרויות:

כדאי לחתוך את פיסת הבד אפקית באיזשהו $\displaystyle i'$ . במקרה זה נקבל שתי חתיכות בד, האחת במידות $\displaystyle (i',j)$ ,‏ והשניה במידות $\displaystyle (i-i',j)$ . עפ"י ההגדרה, הטוב ביותר שאפשר להשיג עבור הראשונה הוא $\displaystyle m(i',j)$ ,‏ ועבור השניה $\displaystyle m(i-i',j)$ .
כדאי לחתוך את פיסת הבד אנכית באיזשהו $\displaystyle j'$ . במקרה זה נקבל שתי חתיכות בד, האחת במידות $\displaystyle (i,j')$ ,‏ והשניה במידות $\displaystyle (i,j-j')$ . עפ"י ההגדרה, הטוב ביותר שאפשר להשיג עבור הראשונה הוא $\displaystyle m(i,j')$ ,‏ ועבור השניה $\displaystyle m(i,j-j')$ .
כלל לא משתלם לחתוך את פיסת הבד: הטוב ביותר האפשרי הוא Value(i, j).

היות שאיננו יודעים איזו משלוש האפשרויות היא הטובה ביותר, אנו לוקחים את המקסימום מבין שלושתן.

מימוש רקורסיבי נאיבי[עריכה]

הפסוודו-קוד הבא מראה מימוש פשוט לנוסחה הנ"ל:

Max-Value(i, j)
1	max-value = 0

	# Check horizontal cuts.

	# This loop means the C-language loop for(i' = 1; i' < i; ++i')
2	for i' in [1, ..., i - 1]
3		guess = Max-Value(i', j) + Max-Value(i - i', j)		
4		if guess > max-value
5			max-value = guess
		
	# Check vertical cuts.

	# This loop means the C-language loop for(j' = 1; j' < j; ++j')
6	for j' in [1, ..., j - 1]
7		guess = Max-Value(i, j') + Max-Value(i, j - j')		
8		if guess > max-value
9			max-value = guess

	# Check the worth of this shape.

19	guess = Value(i, j)
	
11	if guess > max-value
12		max-value = guess

13	return max-value

שימוש בmemoization[עריכה]

כרגיל, נוסיף מבנה נתונים פשוט (במקרה זה המטריצה M) כדי לשמור את הערכים שכבר חישבנו:

1	M = Make-Matrix(m, n)

2	for i in [1, ..., m]
3		for j in [1, ..., n]
4			M[i][j] = Nil


Max-Value(i, j)
1	if M[i, j] != Nil
2		return M[i, j]

4	max-value = 0

	# Check horizontal cuts.

5	for i' in [1, ..., i - 1]
6		guess = Max-Value(i', j) + Max-Value(i - i', j)		
7		if guess > max-value
8			max-value = guess
		
	# Check vertical cuts.

9	for j' in [1, ..., j - 1]
10		guess = Max-Value(i, j') + Max-Value(i, j - j')		
11		if guess > max-value
12			max-value = guess

	# Check the worth of this shape.

13	guess = Value(i, j)
	
14	if guess > max-value
15		max-value = guess
		
16	M[i, j] = max-value

17	return max-value

הדפסת החלטות החיתוך[עריכה]

שוב כרגיל, כדי לשמור גם את סדרת הפעולות (ולא רק תוצאתן), נוסיף עוד מבנה נתונים פשוט (במקרה זה המטריצה C):

1	M = Make-Matrix(m, n)
2	C = Make-Matrix(n, n)

3	for i in [1, ..., m]
4		for j in [1, ..., n]
5			M[i][j] = Nil
6			C[i][j] = Nil


Max-Value(i, j)
1	if M[i, j] != Nil
2		return M[i, j]

3	max-value = 0

	# Check horizontal cuts.

4	for i' in [1, ..., i - 1]
5		guess = Max-Value(i', j) + Max-Value(i - i', j)		
6		if guess > max-value
7			max-value = guess
8			C[i][j] = ('Horizontal', i')
		
	# Check vertical cuts.

9	for j' in [1, ..., j - 1]
10		guess = Max-Value(i, j') + Max-Value(i, j - j')		
11		if guess > max-value
12			max-value = guess
13			C[i][j] = ('Vertical', j')

	# Check the worth of this shape.

14	guess = Value(i, j)
	
15	if guess > max-value
16		max-value = guess
17		C[i][j] = ('Shape', 0)
		
18	M[i, j] = max-value

19	return max-value

המטריצה C היא מטריצה של זוגות (בשפת C היינו ממשים זאת בעזרת מטריצה של מבנים):

האיבר הראשון בכל זוג הוא מחרוזת, המתארת איזו משלוש האפשרויות היא בחרנו.
האיבר השני בכל זוג הוא מספר המתאר היכן חתכנו.

הנה הקוד המדפיס את סדרת הפעולות:

Print-Cuts(i, j)
1	Print('For the best value of ' + i + ' and ' + j)

2	(type, index) = C[i][j]

3	if type == 'Horizontal'
4		Print 'Cut horizontally at ' + index
5		Print-Cuts(index, j)
6		Print-Cuts(i - index, j)
7	else if type == 'Vertical'
8		Print 'Cut vertically at ' + index
9		Print-Cuts(i, index)
10		Print-Cuts(i, j - index)
11	else
12		Print 'Use the shape itself'

ניתוח סיבוכיות[עריכה]

נגדיר כ $\displaystyle T'(i,j)$ את סיבוכיות Max-Cuts(i, j) בהנחה שכל קריאה רקורסיבית היא $\displaystyle O(1)$ . קל מאד לראות מהקוד ש $\displaystyle T'(i,j)=\Theta (i+j)$ . נשים לב גם ש $\displaystyle \Theta (i+j)=O(m+n)$ , ולכן $\displaystyle T'(i,j)=O(m+n)$ . סיבוכיות $\displaystyle Max-Cuts(m,n)$ חסומה מלמעלה על ידי $\displaystyle \sum _{i=1}^{m}\sum _{j=1}^{n}[T'(i,j)]=\sum _{i=1}^{m}\sum _{j=1}^{n}[O(m+n)]=O(m\cdot n\cdot (m+n))$ .

גם כאשר לוקחים בחשבון את האתחול והדפסת הפרטים, הפתרון עדיין $\displaystyle O(m\cdot n\cdot (m+n))$ .