אינטגרל מוכלל (או אינטגרל לא־אמיתי) הנו הכללה של האינטגרל המסוים (רימאן) לקטעים לא־חסומים ופונקציות לא־חסומות.
- דוגמא
חשב את האינטגרל 
![{\displaystyle \int \limits _{-1}^{1}{\frac {dx}{x^{2}}}=\left[-{\frac {1}{x}}\right]_{-1}^{1}=-{\frac {1}{1}}-\left(-{\frac {1}{-1}}\right)=-2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/737b42a046b62e0557e37e258e6b0e7c3b70cb6c)
- הסבר
מה קרה?! הרי הפונקציה  הנה חיובית בכל תחום הגדרתה, ואינטואיטיבית היינו צריכים לקבל שטח חיובי. היכן טעינו?
הנה חיובית בכל תחום הגדרתה, ואינטואיטיבית היינו צריכים לקבל שטח חיובי. היכן טעינו?
טעינו בכמה דברים. הפונקציה לא־רציפה בקטע ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) וגם הגבול
וגם הגבול  לא קיים, כלומר הפונקציה אינה חסומה.
לא קיים, כלומר הפונקציה אינה חסומה.
אינטגרלים מוכללים בקטעים לא-חסומים
[עריכה]תהי  פונקציה אינטגרבילית בקטע
פונקציה אינטגרבילית בקטע ![{\displaystyle [a,M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5753d5e8a5eb338c7cef7c846240fbd147be194) לכל
לכל  .
.
נגדיר:  בתנאי שהגבול קיים (וסופי). אם הגבול אינו קיים אזי האינטגרל מתבדר.
בתנאי שהגבול קיים (וסופי). אם הגבול אינו קיים אזי האינטגרל מתבדר.
באופן דומה נגדיר: 
- דוגמא 1
חשב את האינטגרל של הפונקציה  בקטע
בקטע 
הפונקציה רציפה בקטע זה, ולכן אינטגרבילית בקטע  . נקבל:
. נקבל:
![{\displaystyle \int \limits _{1}^{\infty }{\frac {dx}{x^{2}}}=\lim _{M\to \infty }\int \limits _{1}^{M}{\frac {dx}{x^{2}}}=\lim _{M\to \infty }-{\frac {1}{x}}{\Bigg |}_{1}^{M}=\lim _{M\to \infty }\left[-{\frac {1}{M}}+{\frac {1}{1}}\right]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40e292dcc48b0a492fb6b77af8a29d8690f3795e)
- דוגמא 2
חשב את האינטגרל של הפונקציה  בקטע
בקטע 
הפונקציה רציפה על כל הישר הממשי ולכן אינטגרבילית, ובפרט בקטע  . נקבל:
. נקבל:
![{\displaystyle \int \limits _{0}^{\infty }e^{-x}dx=\lim _{M\to \infty }\int \limits _{0}^{M}e^{-x}dx=\lim _{M\to \infty }-e^{-x}{\Bigg |}_{0}^{M}=\lim _{M\to \infty }{\Big [}-e^{-M}+e^{-0}{\Big ]}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/526b0627b7a92b054ec291c10acb5e6f9858bb07)
- דוגמא 3
חשב את האינטגרל של הפונקציה  בקטע
בקטע 
הפונקציה רציפה על כל הישר הממשי ולכן אינטגרבילית, ובפרט בקטע  . נקבל:
. נקבל:
![{\displaystyle \int \limits _{0}^{\infty }\cos(x)dx=\lim _{M\to \infty }\int \limits _{0}^{M}\cos(x)dx=\lim _{M\to \infty }\sin(x){\Bigg |}_{0}^{M}=\lim _{M\to \infty }{\Big [}\sin(M)-\sin(0){\Big ]}=\lim _{M\to \infty }\sin(M)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/382f0c65baab20db9d81eae48b87cad668a16c08)
אך הגבול באינסוף לא קיים, ולכן האינטגרל מתבדר.
- אם האינטגרל
 מתכנס, אזי לכל
מתכנס, אזי לכל  מתקיים
מתקיים 
- תהי
 פונקציה אינטגרבילית בכל קטע סגור. אם קיים
פונקציה אינטגרבילית בכל קטע סגור. אם קיים  עבורו
עבורו  מתכנסות, אזי
מתכנסות, אזי  אינטגרבילית ב־
אינטגרבילית ב־ ומתקיים
ומתקיים 
אינטגרלים מוכללים של פונקציות לא־חסומות
[עריכה]תהי  פונקציה לא-חסומה.
פונקציה לא-חסומה.
נגדיר: אם מתקיים  אינטגרבילית בקטע הסגור
אינטגרבילית בקטע הסגור ![{\displaystyle [a,t]\subset [a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66b41a34ef01eedbee2c328840f9220e64b8751e) , אזי
, אזי  בתנאי שהגבול קיים.
בתנאי שהגבול קיים.
עבור המקרה ![{\displaystyle (a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae) נגדיר
נגדיר  בתנאי שהגבול קיים.
בתנאי שהגבול קיים.
אם קיימת נקודה ![{\displaystyle c\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/997256364b06acf0710e5d24da39e8c42991a249) בה
בה  לא חסומה, אזי
לא חסומה, אזי  בתנאי שגבולות האינטגרלים בצד ימין קיימים.
בתנאי שגבולות האינטגרלים בצד ימין קיימים.
- דוגמא 1
חשב את האינטגרל של הפונקציה  בקטע
בקטע ![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4) .
.
![{\displaystyle \int \limits _{0}^{1}{\frac {dx}{\sqrt {x}}}=\lim _{t\to 0^{+}}\int \limits _{t}^{1}{\frac {dx}{\sqrt {x}}}=\lim _{t\to 0^{+}}2{\sqrt {x}}{\Bigg |}_{t}^{1}=\lim _{t\to 0^{+}}{\Big [}2{\sqrt {1}}-2{\sqrt {t}}{\Big ]}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48cdbc6843a661c1ffeba543daf9c8b19409b479)
- דוגמא 2
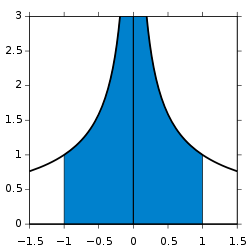
חשב את האינטגרל של הפונקציה ![{\displaystyle f(x)={\frac {1}{\sqrt[{3}]{x^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/508c82aeca868d2899f1503b88f6b91b77a7323c) בקטע
בקטע ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) .
.
הפונקציה לא-חסומה בקטע בסביבת  , כלומר עלינו לחשב את האינטגרל בקטע
, כלומר עלינו לחשב את האינטגרל בקטע ![{\displaystyle [1,0)\cup (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40c800a20c6cd153d3862b92801d2a118f0e256b) .
.
![{\displaystyle {\begin{aligned}\int \limits _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}&=\lim _{t_{1}\to 0^{-}}\int \limits _{-1}^{t_{1}}{\frac {dx}{\sqrt[{3}]{x^{2}}}}+\lim _{t_{2}\to 0^{+}}\int \limits _{t_{2}}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}\\&=\lim _{t_{1}\to 0^{-}}3{\sqrt[{3}]{x}}{\Bigg |}_{-1}^{t_{1}}+\lim _{t_{2}\to 0^{+}}3{\sqrt[{3}]{x}}{\Bigg |}_{t_{2}}^{1}\\&=\lim _{t_{1}\to 0^{-}}{\Big [}3{\sqrt[{3}]{t_{1}}}-3{\sqrt[{3}]{-1}}{\Big ]}+\lim _{t_{2}\to 0^{+}}{\Big [}3{\sqrt[{3}]{1}}-3{\sqrt[{3}]{t_{2}}}{\Big ]}=3+3=6\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e96f485479e3bcad119a837272524b5fb2f169b3)



![{\displaystyle \int \limits _{-1}^{1}{\frac {dx}{x^{2}}}=\left[-{\frac {1}{x}}\right]_{-1}^{1}=-{\frac {1}{1}}-\left(-{\frac {1}{-1}}\right)=-2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/737b42a046b62e0557e37e258e6b0e7c3b70cb6c)

![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)


![{\displaystyle [a,M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5753d5e8a5eb338c7cef7c846240fbd147be194)






![{\displaystyle \int \limits _{1}^{\infty }{\frac {dx}{x^{2}}}=\lim _{M\to \infty }\int \limits _{1}^{M}{\frac {dx}{x^{2}}}=\lim _{M\to \infty }-{\frac {1}{x}}{\Bigg |}_{1}^{M}=\lim _{M\to \infty }\left[-{\frac {1}{M}}+{\frac {1}{1}}\right]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40e292dcc48b0a492fb6b77af8a29d8690f3795e)



![{\displaystyle \int \limits _{0}^{\infty }e^{-x}dx=\lim _{M\to \infty }\int \limits _{0}^{M}e^{-x}dx=\lim _{M\to \infty }-e^{-x}{\Bigg |}_{0}^{M}=\lim _{M\to \infty }{\Big [}-e^{-M}+e^{-0}{\Big ]}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/526b0627b7a92b054ec291c10acb5e6f9858bb07)

![{\displaystyle \int \limits _{0}^{\infty }\cos(x)dx=\lim _{M\to \infty }\int \limits _{0}^{M}\cos(x)dx=\lim _{M\to \infty }\sin(x){\Bigg |}_{0}^{M}=\lim _{M\to \infty }{\Big [}\sin(M)-\sin(0){\Big ]}=\lim _{M\to \infty }\sin(M)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/382f0c65baab20db9d81eae48b87cad668a16c08)










![{\displaystyle [a,t]\subset [a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66b41a34ef01eedbee2c328840f9220e64b8751e)

![{\displaystyle (a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)

![{\displaystyle c\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/997256364b06acf0710e5d24da39e8c42991a249)


![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4)
![{\displaystyle \int \limits _{0}^{1}{\frac {dx}{\sqrt {x}}}=\lim _{t\to 0^{+}}\int \limits _{t}^{1}{\frac {dx}{\sqrt {x}}}=\lim _{t\to 0^{+}}2{\sqrt {x}}{\Bigg |}_{t}^{1}=\lim _{t\to 0^{+}}{\Big [}2{\sqrt {1}}-2{\sqrt {t}}{\Big ]}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48cdbc6843a661c1ffeba543daf9c8b19409b479)
![{\displaystyle f(x)={\frac {1}{\sqrt[{3}]{x^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/508c82aeca868d2899f1503b88f6b91b77a7323c)

![{\displaystyle [1,0)\cup (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40c800a20c6cd153d3862b92801d2a118f0e256b)
![{\displaystyle {\begin{aligned}\int \limits _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}&=\lim _{t_{1}\to 0^{-}}\int \limits _{-1}^{t_{1}}{\frac {dx}{\sqrt[{3}]{x^{2}}}}+\lim _{t_{2}\to 0^{+}}\int \limits _{t_{2}}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}\\&=\lim _{t_{1}\to 0^{-}}3{\sqrt[{3}]{x}}{\Bigg |}_{-1}^{t_{1}}+\lim _{t_{2}\to 0^{+}}3{\sqrt[{3}]{x}}{\Bigg |}_{t_{2}}^{1}\\&=\lim _{t_{1}\to 0^{-}}{\Big [}3{\sqrt[{3}]{t_{1}}}-3{\sqrt[{3}]{-1}}{\Big ]}+\lim _{t_{2}\to 0^{+}}{\Big [}3{\sqrt[{3}]{1}}-3{\sqrt[{3}]{t_{2}}}{\Big ]}=3+3=6\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e96f485479e3bcad119a837272524b5fb2f169b3)