מבני נתונים ואלגוריתמים - מחברת קורס/שיעורי בית 3/שאלות

שימו לב: *נא להגיש רק את שאלות 1-5. שאר השאלות הן לצורך חזרה למבחן בלבד. אין צורך להגיש את התשובות להן.

1

כדאי לדעת: שאלה זו עוסקת באלגוריתם המיון Quicksort - אלגוריתם מיון מהיר ונפוץ-שימוש מאד. את מהירות האלגוריתם בפועל מקנים הסברים הסתברותיים וטריקים טכניים המייצרים לולאות פשוטות ומהירות מאד. לא נלמד על שני נושאים אלה בקורס (המעוניינים יכולים לקרוא עוד בדף Quicksort.

להלן מימוש אפשרי לפונקציה Partition. הפונקציה מקבלת מערך (Values), אינדקס התחלה (b), ואינדקס סוף (e). אם לפני הקריאה לפונקציה [v == Values[b הוא הערך שישב במקום b, אז הפונקציה תארגן מחדש את המערך ותחזיר ערך p, כך שValues[b, ..., p] מכיל אך ורק איברים קטנים או שווים לv, וValues[p + 1, ..., e] מכיל אך ורק איברים גדולים או שווים לv.

# Partitions an array (Values) between begining (b) and end (e) indexes.
# Returns the partition index p (b <= r < e).
# If v == Values[b] originally, then after calling this function:
#	any value in Values[b, ..., p] is <= v,
#	any value in Values[p + 1, ..., e] is >= v
Partition(Values, b, e)
1	v = Values[b]
	
2	l = b - 1
3	r = e + 1
	
4	while True		
5		do
6			--r
7		while value < Values[r]
	
8		do
9			++l
10		while value > Values[l]
								
11		if l >= r
12			return r			
	
13		// Exchange Values[l] with Values[r]
14		Values[l] <-> Values[r]

שימו לב: אין צורך להתעמק בפסוודו-קוד של Partition. רפרף עליו באופן כללי, ובהמשך הנח את הדברים הבאים: הפונקציה עובדת נכון, דהיינו היא אכן מארגנת את המערך ומחזירה ערך p לפי ההסבר שלמעלה. אם p = Partition(Values, b, e), אז $\displaystyle b\leq p<e$. סיבוכיות הפונקציה היא לינארית באורך הקטע, דהיינו $\displaystyle \Theta (b-e+1)$ (בכל מקרה: טוב או רע).

פונקציית המיון Quicksort מוגדרת בעזרת Partition באופן הבא:

# Sorts an array (Values) from a begining index (b) to 
#	an end index (e), through successive partitioning.
Quicksort(Values, b, e)
1	if b >= e
2		return
	
	# Choose a random number between b and e.
3	r = Random(b, e)
	# Exchange Values[b] with Values[r]
4	Values[b] <-> Values[r]	

5	p = Partition(Values, b, e)

6	Quicksort(Values, b, p)
7	Quicksort(Values, p + 1, e)

בפונקציה זו, 3 בוחרת מספר אקראי בין b לe (לדוגמה, אם b == 1 וe == 3, אז ייבחר $\displaystyle 1$,‏ $\displaystyle 2$,‏ או $\displaystyle 3$). (הנח שסיבוכיות Random היא $\displaystyle O(1)$.) ‏ 4 מחליפה בין איבר אינדקס ההתחלה לאיבר האינדקס האקראי שנבחר. 5 קוראת לPartition שראינו, דבר שמחלק את המערך לשני חלקים. 6 ו7 קוראות רקורסיבית לפונקציה על כל אחד משני החלקים.

1. אנא הוכח את נכונות הפונקציה Quicksort. דהיינו, הוכח שQuicksort(Values, 1, Length(Values)) אכן תמיין את Values.
2. הנח שהפונקציה מופעלת על מערך בעל איברים שונים זה מזה. נניח שאיתרע מזלנו, וRandom(b, e) (בשורה 3) מחזירה תמיד את אינדקס האיבר הקטן ביותר בין b לe. אנא נתח את סיבוכיות המיון במקרה זה.
3. הנח שהפונקציה מופעלת על מערך בעל איברים שונים זה מזה. נניח שאיתרע מזלנו, וRandom(b, e) (בשורה 3) מחזירה תמיד את אינדקס האיבר שחצי מהאיברים בין b לe גדולים ממנו (התעלם משגיאות עיגול). אנא נתח את סיבוכיות המיון במקרה זה.

2

נתון מערך A המכיל $\displaystyle n$ מספרים, כל אחד בתחום $\displaystyle [1,...,k]$‏ ($\displaystyle k$ מספר שלם כלשהו). רוצים לענות מספר רב של פעמים על שאלות מהסוג: בהינתן $\displaystyle a$ ו$\displaystyle b$ כלשהם, כמה מ$\displaystyle n$ האיברים בA נמצאים בתחום $\displaystyle [a,...,b]$? לצורך כך רוצים לכתוב שתי פונקציות:

1. Init מקבלת את המערך A והערך $\displaystyle k$, ומבצעת פעולות אתחול כלשהן.
2. Range מקבלת שני מספרים a וb, ומחזירה כמה מאיברי A נמצאים בין שני המספרים.להלן דוגמה לשימוש אפשרי:

1	A = [1, 3, 2, 3, 3, 3, 15, 3]

	# Initializes whatever is needed
2	Init(A, 15)

	# Prints 8.
3	Print( Range(1, 16) )

	# Prints 1.
4	Print( Range(1, 1) )

	# Prints 1.
5	Print( Range(2, 2) )

	# Prints 7.
6	Print( Range(1, 14) )

אנא כתוב מימוש יעיל ככל האפשר לשתי הפונקציות, ונתח אותן. (נסה להגיע לכך שRange בזמן $\displaystyle O(1)$.) הוסף משתנים גלובליים ופונקציות עזר כרצונך.

3

אנא וודא את הנוסחות הבאות בזמן הריצה של הכפלת שרשרת מטריצות תחת memoization:

1. $\displaystyle T'(i,j)=\Theta (j-i+1)$ (נזכר ש$\displaystyle T'(i,j)$ מוגדרת כזמן שאורכת Min-Time(i, j) בהנחה שכ"א מהקריאות הרקורסיביות היא $\displaystyle O(1)$).
2. $\displaystyle T(1,n)=\sum _{i=1}^{n}\sum _{j=i}^{n}[T'(i,j)]$.
3. $\displaystyle T(1,n)=\Theta (n^{3})$.

4

בבעיית "תכנון הפרוייקטים" יש $\displaystyle k$ פרוייקטים ו$\displaystyle n$ עובדות. צריך להחליט כמה עובדות יש להקצות לכל אחד מהפרוייקטים.

לכל פרוייקט $\displaystyle 1\leq i\leq k$ ומספר עובדות $\displaystyle 1\leq j\leq n$, ‏ $\displaystyle q(i,j)$ הוא מספר המייצג את איכות ביצוע הפרוייקט ה$\displaystyle$i אם ישבצו לו $\displaystyle j$ עובדות. הנח:

1. $\displaystyle q(i,j)$ פונקציה לא שלילית (אין איכות שלילית).
2. $\displaystyle q(i,j)$ מונוטונית לא-יורדת ב$\displaystyle j$ (הוספת עובדות לפרוייקט אינה מורידה מאיכותו).
3. ניתן להקצות 0 עובדות לפרוייקט.
4. כל עובדת מוקצת לפרוייקט אחד בדיוק.

לכל פרוייקט $\displaystyle i$ יש "חשיבות" לא-שלילית $\displaystyle h(i)$. אנו רוצים למקסם את סך האיכויות המשוקללות. במילים אחרות, אנו רוצים למקסם את $\displaystyle \max _{i_{1},i2,\ldots ,i_{n}:i_{1}\geq 0,\ldots ,i_{n}\geq 0,i_{1}+\cdots +i_{n}=n}\sum \left[h(i)q(i,j)\right]$.

אנא הצע אלגוריתם יעיל לפתרון הבעיה, כלומר אלגוריתם שימצא את הסכום הנ"ל המקסימלי וכן ידפיס את אופן הקצאת העובדות לכל פרוייקט. הנח שq(i, j) וh(i) הן פונקציות נתונות לך, שעלות קריאה להן היא $\displaystyle O(1)$.

5

מעל הירקון עומד גשר שאורכו $\displaystyle m$ מטרים ($\displaystyle m$ מספר שלם חיובי גדול מ1 כלשהו). הגשר נמצא לא תקין אפילו בסטנדרטים של מדינת ישראל(!). יש לפרק את הגשר לחלקים ולפנותו בצורה הזולה ביותר. ראשית צריך לשבור את הגשר. ניתן לשבור את הגשר למספר חלקים. שבירת הגשר חייבת להתבצע בנקודות $\displaystyle 1,\cdots ,m-1$ בלבד. שבירת כל נקודה עולה $\displaystyle k$ שקלים ($\displaystyle k$ מספר שלם חיובי כלשהו).

דוגמה: נניח $\displaystyle m=3$ ו$\displaystyle k=100$ (ראה A בתרשים הבא). אפשר לשבור את הגשר ב4 אפנים: שוברים בנקודות 1 ו2. מתקבלים 3 חלקים בעלי אורך 1 כל אחד (ראה B בתרשים הבא). עלות השבירה היא $\displaystyle 2\cdot 100=200$. שוברים בנקודה 1. מתקבלים 2 חלקים: הראשון בעל אורך 1, והשני בעל אורך 2 (ראה C בתרשים הבא). עלות השבירה היא $\displaystyle 1\cdot 100=100$. שוברים בנקודה 2. מתקבלים 2 חלקים: הראשון בעל אורך 2, והשני בעל אורך 1 (ראה D בתרשים הבא). עלות השבירה היא $\displaystyle 1\cdot 100=100$. לא שוברים באף נקודה. מתקבל חלק יחיד בעל אורך 3. עלות השבירה היא $\displaystyle 0\cdot 100=0$. דוגמה לגשר הזבלה.

כעת יש להוביל את חלקי הגשר. הנח שקיימת פונקציה $\displaystyle f$ ידועה כך ש$\displaystyle f(i)$ מתארת את עלות הובלתו של חלק בעל אורך i. הנח ש$\displaystyle f(i)$ הוא מספר שלם חיובי לכל $\displaystyle i$.

שימו לב: וודא שאינך מניח במובלע דברים שלא נאמרו לגבי $\displaystyle f(i)$. בפרט, אל תניח שהפונקציה מונוטונית עולה (עלות ההובלה נקבעת לפי שיקולים שאיננו יודעים.)

דוגמה: בהמשך לדוגמה הקודמת שראינו, נניח $\displaystyle f(1)=1$,‏ $\displaystyle f(2)=10$,‏ ו$\displaystyle f(3)=2$. ארבע האפשרויות שראינו מקודם יעלו כך: עלות ההובלה היא $\displaystyle f(1)+f(1)+f(1)=3$. עלות ההובלה היא $\displaystyle f(1)+f(2)=11$. עלות ההובלה היא $\displaystyle f(2)+f(1)=11$. עלות ההובלה היא $\displaystyle f(3)=2$.

אנא מצא אלגוריתם יעיל למציאת נקודות השבירה כך שסך העלויות (שבירה והובלה) נמוך ככל האפשר. כלומר, אנא כתוב אלגוריתם יעיל שימצא את העלות המינימלית וכן ידפיס את נקודות השבירה של עלות זו.

6

‫אלגוריתם ‪ Selection-Sort‬פועל באופן הבא: הוא מחפש את האיבר הקטן ביותר במערך ומחליף אותו באיבר‬ ‫הראשון, אח"כ מחפש את האבר הקטן ביותר מבין כל שאר האיברים ומחליף אותו באיבר השני, ובאופן דומה‬ ‫ממשיך להחליף עד שמסיים.

אנא כתבו את הפסוודו-קוד לאלגוריתם, הוכחו נכונותו, ונתחו את סיבוכיותו.

7

הגדרה: (הנוסע המתמיד האוקלידי) נתונות $\displaystyle n$ נקודות במישור. כל נקודה מייצגת שדה תעופה, לצורך העניין. סוכן נסיעות מתחיל את מסלולו בשדה התעופה השמאלי ביותר; עליו לעבור בכל שדה תעופה ולנחות בשדה התעופה שממנו יצא לדרכו. מחיר הטיסה משדה תעופה אחד לשני הוא המרחק האוקלידי בין שני השדות. על הנוסע למצוא את המסלול שעלותו הכוללת נמוכה ככל האפשר.

כדאי לדעת: לבעיית הנוסע המתמיד האוקלידי אין אלגוריתם יעיל ידוע - כל האלגוריתמים הידועים עובדים בזמן אקספוננציאלי. למרות שהדבר לא הוכח, יש סיבות המרמזות לכך שלא ייתכן אלגוריתם יעיל לבעיה זו.

שאלה זו דנה בגרסה קלה יותר של הבעיה.

הגדרה: (מסלול ביטוני) מסלול הוא ביטוני אם הוא מורכב משני תתי מסלולים: בראשון נעים בכיוון ימין, ובשני נעים מימין חזרה לכוון שמאל.

דוגמה: בתרשים הבא, A מראה מישור בעל $\displaystyle n=7$ נקודות; B מראה את המסלול הקצר ביותר, אך המסלול אינו ביטוני. 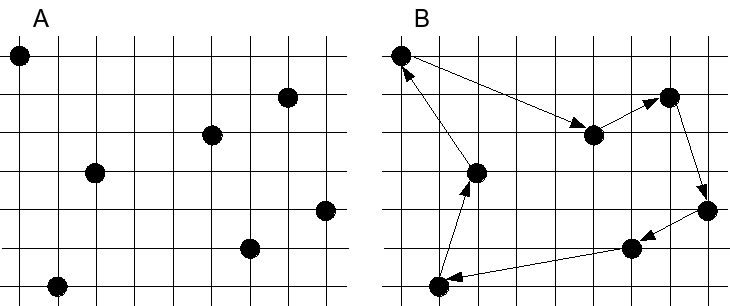מישור ומסלולים. בתרשים הבא, A וB מראים כל אחד מסלול ביטוני אפשרי. מסלולים ביטוניים.

בשאלה זו עליך למצוא אלגוריתם למציאת המסלול הביטוני האוקלידי הזול ביותר לכל קבוצת נקודות במרחב: אנא תאר אלגוריתם יעיל המוצא את עלות המסלול הנמוכה ביותר.

שימו לב: #הנח שP הוא מערך גלובלי בעל אורך $\displaystyle n$ המתאר את הנקודות. כדי לגשת לקואורדינטות הX והY של הנקודה ה$\displaystyle i$, השתמש בP[i].x ובP[i].y, בהתאמה. הנח שP ממוין בסדר עולה על פי קואורדינטות הX של נקודותיו (ולכן P[1] היא בהכרח נקודת המוצא של הנוסע, לדוגמה). אנא נתח סיבוכיות תשובתך במונחי $\displaystyle n$.