מבני נתונים ואלגוריתמים - מחברת קורס/מבחן סופי מועד ב' סמסטר ב' 2007 - תשובות
הבהרה בנוגע לשימוש בלשון זכר: כדי למנוע סרבול מיותר, וכמקובל בשפה העברית, ננקטת לעתים לשון זכר בהתייחסות אל כלל הגולשות והגולשים ובמתן שמות לערכים. אנא קבלו זאת בהבנה.
שאלה 1
[עריכה]תוכל לראות הסבר לגבי המבנה הרקורסיבי של הבעיה בפרק המדבר על חשיבה רקורסיבית
נפתור את הבעיה בשני אופנים: מלמטה למעלה, ומלמעלה למטה.
פתרון מלמטה למעלה
[עריכה]Subset-Sum(A, t)
1 Sum = Make-Array(t)
2 for j in [t … 1]
3 Sum[j] = False
4 n = Length(A)
5 for i in [1, … n]
6 for j in [t … 1]
7 if j== A[i]
8 Sum[j] = True
9 if t > A[i] and Sum[t - A[i]] == True
10 Sum[j] = True
11 return Sum[t] == True
1-3 מייצרות מערך Sum באורך , ומאתחלות את כל איבריו לFalse. הלולאה 5-10 עוברת על כל איברי A. לכל איבר כזה, 6-10 מעדכנת לTrue כל תא בSum שברור שניתן להגיע אליו מסכום האיברים שנבדקו עד כה. כל שנותר ב11 הוא להחזיר האם ניתן להגיע לסכום t.

|
שימו לב: חשוב שהלולאה ב6 תהיה בסדר יורד. אותה הלולאה בסדר עולה תניב פתרונות שגויים. |
קל לראות שהסיבוכיות היא .
פתרון מלמעלה למטה
[עריכה]Subset-Sum(A, i, t')
1 if t == 0
2 return True
3 if i == 0
4 return False
5 if SS[i, t'] != Nil
6 return SS[i, t']
7 if Subset-Sum(A, i - 1, t') == True
8 SS[i, t'] = True
9 return True
10 if t' ≥ A[i] and Subset-Sum(A, i - 1, t' - A[i]) == True
11 SS[i, t'] = True
12 return True
13 SS[i, t'] = False
14 return False
(נניח שSS היא מטריצה בעלת שורות ו עמודות, המאותחלת כולה לNil. בנייתה תארך .)
סיבוכיות הפתרון שוב פעם : אתחול המטריצה עולה . כמו כן, נגדיר כ את זמן הריצה של Subset-Sum(i, t') בהנחה שכל קריאה רקורסיבית אורכת . קל לראות ש. הסיבוכיות הכוללת של הקריאות היא .
שאלה 2
[עריכה]תשובה שגויה ע"י שימוש באלגוריתם Kruskal
[עריכה]כדאי לדעת: אלגוריתם Kruskal פועל כך. ראשית הוא ממיין את קשתות הגרף על פי העלות (או המשקל, תלוי בהגדרה), ולאחר מכן הוא בוחר קשתות מעצים שונים על פי סדר המיון. |
להלן הוכחה שגויה לקיום עפ"מ יחידי:
הוכחה: נשים לב שאם הקשתות בעלות משקלים שונים, תוצאת המיון נקבעת חד משמעית, ולכן יש רק עפ"מ יחיד שאלגוריתם Kruskal יחזיר. לכן יש עפ"מ יחיד.
תשובה זו אינה נכונה, מפני שהיא מתייחסת לאלגוריתם Kruskal בלבד. אפשר עדיין לטעון, לדוגמה, שאלגוריתם Prim יחזיר עפ"מ שונה במקרה זה (בהמשך נראה שזה בלתי אפשרי, אלא שאי אפשר להסיק זאת מהטענה שהוצגה עד עתה).
תשובה שגויה ע"י שימוש לא נכון באינדוקציה
[עריכה]להלן הוכחה שגויה באינדוקציה:
הוכחה: האינדוקציה היא על מספר הצמתים, .
(בסיס האינדוקציה) כאשר אז יש צומת יחיד והעפ"מ בוודאי יחידי.
(מעבר האינדוקציה), ניקח צומת כלשהו , ונמצא את העפ"מ של הצמתים . קבוצה זו קטנה ב1 מ, ולכן יש לה עפ"מ יחידי. נותר לחבר את ל, וברור שנעשה זאת דרך הקשת הזולה ביותר בין לבין צומת ב.
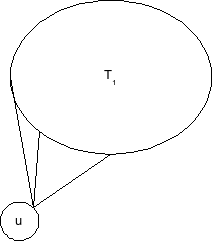
מדוע ההוכחה שגויה? היא מוכיחה שיש עפ"מ יחיד מבין העפ"מים בהם יוצאת קשת יחידה מ. היא כלל אינה סותרת את קיומו של עפ"מ כמו בתרשים הבא, שלכאורה יכול להיות אופטימאלי גם כן:
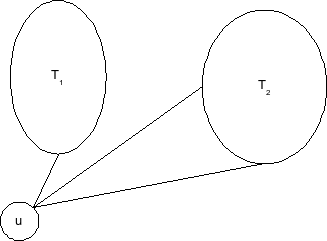
כדאי לדעת: חדי העין יזהו שאין הבדל ממשי בין הטעות כאן לבין הטעות הקודמת. האינדוקציה כאן היא למעשה הפעלת אלגוריתם Prim תחת הנחות שגויות שמקבלת תוצאה כללית לגבי כל העפ"מים האפשריים. |
תשובה ע"י שיקול הקשת הזולה ביותר בגרף
[עריכה]ראשית נוכיח את המשפט הבא.
הוכחה: ראשית ברור שהתוצאה היא עץ. נניח ש ו הם שני צמתים. קל לראות שאם יש מסלול מ ל ב המשתמש בקשתות בלבד , אז יש מסלול מ ל ב המשתמש בקשתות בלבד. קל לראות שאם מכיל מעגל, אז גם מכיל מעגל.
כעת ברור גם שמדובר בעץ הזול ביותר. נניח שיש עץ פורש זול יותר . אז גם עץ פורש זול יותר ב, דבר שסותר את הנחתנו ש היא קבוצת קשתות עפ"מ.
בעזרת המשפט הקודם נוכל להוכיח שיש עפ"מ יחידי באינדוקציה (הפעם בצורה נכונה).
הוכחה: האינדוקציה היא על מספר הצמתים, .
(בסיס האינדוקציה) כאשר אז יש צומת יחיד והעפ"מ בוודאי יחידי.
(מעבר האינדוקציה) ניקח את הקשת הקלה ביותר בגרף . כבר הוכחנו שקשת זו היא חלק מכל עפ"מ. כעת "נכווץ" את הגרף ע"י הפיכת שני הצמתים, ו, לצומת יחיד. מהנחת האינדוקציה נובע שקיים כעת עפ"מ יחיד (שהרי מספר הצמתים ירד ב1). המשפט הקודם אומר שקשתות כל עפ"מ שהתקבל בגרף המכווץ, יחד עם , הן בדיוק קשתות העפ"מ בגרף המקורי. נובע לכן שיש עפ"מ יחיד.
תשובה ע"י שיקול הקשת היקרה ביותר במעגל
[עריכה]נניח בשלילה שיש שני עפ"מים שונים: ו. היות שהעפ"מים שונים אך מספר קשתותיהם שווה, קיימת בהכרח קשת השייכת ל אך לא ל. הוספת קשת זו ל בהכרח תיצור מעגל. נגדיר כ את הקשת הכבדה ביותר על פני המעגל, וניזכר שקשת זו איננה חלק מאף עפ"מ. כעת אם , אז אינה עפ"מ; מצד שני, אם , אז אינה עפ"מ. בכל מקרה, לא ייתכן מעגל כזה, ולכן בהכרח אין שני עפ"מים שונים.
שאלה 3
[עריכה]נתבונן בעמודה האחרונה, ונספור את מספר ה0-ים ומספר ה1-ות שאנו רואים. היות שיש , שורות, אז מספר ה0-ים גדול ב1 ממספר ה1-ות, או הפוך. נניח שמספר ה0-ים גדול ב1 ממספר ה1-ות (המקרה השני סימטרי). נוכל להסיק שני דברים:
- הספרה החסרה בעמודה זו היא 1.
- עלינו להתמקד רק בשורות בהן הספרה בעמודה זו היא 1 (קומבינטורית, לא ייתכן אחרת).כעת נתחיל את הבעיה מחדש, תוך התמקדות בחצי (בערך) מהשורות (רק אלה בהן הספרה בעמודה זו היא 1): נסתכל בעמודה הלפני אחרונה,נספור את מספר ה0-ים ומספר ה1-ות שאנו רואים , וכולי.
להלן פסוודו-קוד יעיל המממש זאת:
Print-Missing-Number(M)
1 n = Num-Cols(M)
2 Rows = Make-Stack()
3 for j in [1, … 2^n - 1]
4 Insert-Front(Rows, j)
5 for i in [1, … n]
6 Zeros = Make-Stack()
7 Ones = Make-Stack()
8 while Size(Rows) > 0
9 row = Pop(Rows)
10 if M[row][i] == 0
11 Push(Zeros, row)
12 else
13 Push(Ones, row)
14 if Size(Zeros) > Size(Ones)
15 Print(1)
16 Rows = Ones
17 else
18 Print(0)
19 Rows = Zeros
1-4 מאתחלות את ה[[מבני נתונים ואלגוריתמים - מחברת קורס/#|]] Rows כך שתכיל את כל (מספרי השורות). 5-19 עובורת על כל העמודות. בכל איטרציה, 8-13 מחלקות את מספרי השורות בRows לשתי מחסניות, לפי ערך ביט העמודה הנכחית. 14-19 מדפיסות את הביט החסר בעמודה הנכחית, ומחליטות באיזו משתי המחסניות להתמקד.
נותר לנתח הסיבוכיות. נשים לב שהאיטרציה הראשונה פועלת בזמן , האיטרציה השניה בזמן , ובאופן כללי, האיטרציה ה בזמן . זמן הריצה, לכן, הוא
שאלה 4
[עריכה]- סעיף זה הוא טריביאלי. נשתמש ברשימה מקושרת דו-כוונית (ייתכנו מימושים אחרים, כמובן).
Insertתקרא לInsert-Frontשל רשימה מקושרת, ותעבוד בזמן . אתMinוDelete-Minנממש בעזרת לולאות על חוליות הרשימה. סיבוכיות כל אחת מפעולות אלה תהיה לינארית במספר החוליות במקרה הגרוע. - נזכר שבהנתן תור קדימויות, ניתן לממש בעזרת סידרת פעולות
Insertולאחריה סידרת פעולותDelete-Min(באופן כמעט זהה לHeapsort). לו כל פעולה היתה עובדת בזמן , אז ניתן היה למיין בזמן לינארי, בניגוד לחסם התחתון על מיון מבוסס-השוואות שלמדנו.
שאלה 5
[עריכה]נוכיח את הטענה באינדוקציה על , מספר הצמתים.
(בסיס האינדוקציה) אם בגרף יש צומת יחיד, אין קשתות. אם בגרף יש שני צמתים, אז או שיש קשת אחת, או שאין אף קשת. בכל אחד ממקרים אלה, בדיקה פשוטה מראה שהטענה מתקיימת. לכן הטענה נכונה עבור .
(מעבר האינדוקציה) נניח שהטענה נכונה עבור כל גרף בעל צמתים, ונראה שהטענה נכונה עבור כל גרף בעל צמתים. ניקח גרף בעל צמתים, ונחפש צומת שמספר שכניו אי-זוגי. (אם אין צומת כזה, הטענה בהכרח נכונה לגרף זה.) נניח ששכניו של הם . נשים לב ש בהכרח אי-זוגי. אם נמחק את והקשתות שיוצאות ממנו, הטענה נכונה מהנחת האינדוקציה. לאחר הוספת מחדש, כמה צמתים בעלי דרגה אי-זוגית נוצרו? עצמו תורם 1. כל שכן של בעל דרגה זוגית הופך להיות בעל דרגה אי-זוגית, וכל שכן של בעל דרגה אי-זוגית הופך להיות בעל דרגה זוגית. היות ש אי-זוגי, תרומת שכניו היא מספר אי-זוגי (חיובי או שלילי). לכן נוצר עוד מספר זוגי (חיובי או שלילי) של צמתים בעלי דרגה זוגית.








![{\displaystyle \displaystyle \sum _{i=1}^{n}\sum _{t'=1}^{t}\left[T'(i,t')\right]=\sum _{i=1}^{n}\sum _{t'=1}^{t}\left[O(1)\right]=\Theta \left(n\cdot t\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3d3798518d9ff1638700349f89bde00c116d28e)




































![{\displaystyle \displaystyle \sum _{i=1}^{n}\left[\Theta (m/2^{i})\right]=\Theta (m).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/674bbdd5be994b9fe4309fba3ac53d4ee92edd88)






