מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/אלגוריתמי זרימה/תרגילים/רשת זרימה שלמה/תשובה
1
[עריכה]הטענה נכונה.
נתבונן בהוכחה של אלגוריתם Ford-Fulkerson. ההוכחה מניחה שכל הקיבולים שלמים (כמו במקרה שלנו), ומגיעה למסקנה שבכל שיפור (כולל השיפור האחרון), הזרימות עדיין שלמות (מה שצריך להוכיח כאן).
2
[עריכה]הטענה אינה נכונה.
להלן דוגמה נגדית.

ברשת הזרימה הזו, קל מאד לראות שהזרימה המירבית בגודל 1.
להלן זרימה בגודל 1 שאינה זרימה שלמה:


|
שימו לב: הדוגמה הנגדית לסעיף זה אינה סותרת את הסעיף הקודם. אכן יש זרימה מירבית שהיא שלמה, כפי שהתרשים הבא מראה:
 |
3
[עריכה]הטענה נכונה.
נתבונן בחתך כלשהו בגרף. מספר הקשתות שחוצות אותו (מ ל) הוא לכל היותר . על פי נתוני השאלה, כל אחד מקיבולי הקשתות קטן מ7. לכן, קיבול החתך הוא לכל היותר . היות שהדבר נכון לכל חתך, הוא נכון גם לחתך הקטן ביותר (מבחינת גודל הקיבול). לכן, עפ"ׁי המשפט Max-Flow Min-Cut, גודל הזרימה המירבית הוא לכל היותר . היות שכל אחד מקיבולי הקשתות הוא מספר שלם, אז כל איטרציה של אלגוריתם ford-Fulkerson תשפר את הזרימה בלפחות 1. מספר האיטרציות לכן הוא לכל היותר .
4
[עריכה]הטענה אינה נכונה.
להלן דוגמה נגדית. התרשים הבא מראה גרף רשת זרימה. הגרף מורכב למעשה משני גרפים זרים. הראשון מכיל 4 צמתים ו5 קשתות. הגרף מכיל עוד מספר צמתים וקשתות בעלי קיבולים שונים (שאינם מענייננו).
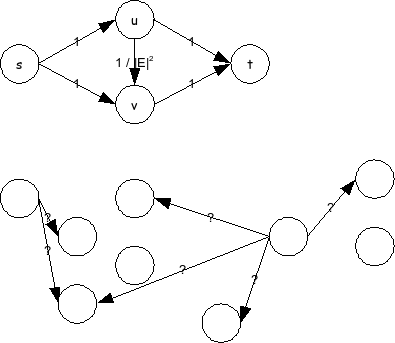
קל לראות שהזרימה המירבית בעלת גודל 2. להלן זרימה כזאת (מכאן ועד סוף השאלה לא נצייר את כל הצמתים והקשתות בגרף):

נניח שהמסלול המשפר הראשון שבחרנו הוא (ולכן הזרימה בסוף האיטרציה הראשונה היא בגודל ). התרשים הבא מראה את גרף הרשת השיורית בשלב זה.

מתרשים זה אפשר לראות שיש כעת שיפור שגם הוא בעל גודל :
השיפור דרך המסלול < math dir = "ltr">\displaystyle s \rightarrow v \rightarrow u \rightarrow t</math> (ולכן הזרימה בסוף האיטרציה השניה היא בגודל ).
קל להראות (פורמלית, באינדוקציה), שאפשר לבצע שיפורים (בזוגות), כך שכל שיפור אי-זוגי יהיה דרך , כל שיפור זוגי יהיה דרך , וגודל הזרימה יהיה .
היות שגודל הזרימה המירבית הוא 2, אז מספר האיטרציות הוא פתרון המשוואה , ולכן .













