מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/אלגוריתמי זרימה/תרגילים/יריד תעסוקה 1/תשובה
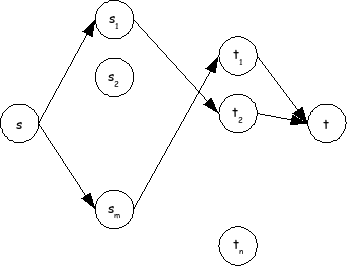
ראשית נבנה את רשת הזרימה המתוארת בתרשים הבא. בגרף זה צמתים:
- צמתים , אחד לכל סטודנט
- צמתים , אחד לכל חברה
- צומת מקור וצומת בור
נגדיר כ את Length(W).
בגרף יש קשתות:
- קשת אחת לכל איבר ב
W - קשת מ לכל
- קשת מכל לקיבולי כל אחת מהקשתות הוא 1.

כעת נריץ את אלגוריתם Ford-Fulkerson. נחזיר כתשובה כל זוג שעבורו קיבלנו .
|
משפט: האלגוריתם מחזיר תשובה נכונה. |
הוכחה: אנו יודעים שאלגוריתם Ford-Fulkerson משפר תמיד בגדלים שלמים (שהרי הקיבולים שלמים). קל מאד להוכיח (פורמלית, באינדוקציה), שבמקרה זה, חלק מהקשתות יזרימו 1, והשאר 0 (אלו האפשרויות היחידות). נצייר את הגרף המתקבל ממחיקת הקשתות שאינן מזרימות כלום:
נניח שיש קשת בין ל. בהכרח הקשת מזרימה 1. מצד שני, הקשת המזרימה מ ל מזרימה גם היא 1. משימור הזרם נובע אם כן שאין קשת אחרת היוצאת מ. טענה כמעט זהה מראה שאין קשת אחרת הנכנסת ל. ברור גם שקשת זו היתה שייכת לגרף המקורי. מכאן נובע שהמערך המוחזר W' אכן משייך אחת לאחת סטודנט לחברה, ואינו ממציא שיוכים שלא הופיעו במקור.
נסמן כ את גודל W'. מניין לנו שאין התאמה גדולה יותר? נניח בשלילה שיש כזו, ונסמן את גודלה כ. אבל, מכאן נובע בהכרח (בסתירה לנכונות Ford-Fulkerson) שיש זרימה בגודל בגרף החדש: קל למצוא קשתות מ לצמתי הסטודנטים, ומצמתי החברות ל, ובדיקה פשוטה של חוקי הזרימה החוקית מראים שאם מזרימה יחידה 1 בכל אחת מקשתות אלו, אז זו אכן זרימה חוקית.
|
משפט: סיבוכיות האלגוריתם . |
הוכחה: אם משתמשים ברשימת שכנויות, אז בניית הגרף החדש היא .כבר ראינו בניתוח אלגוריתם Ford-Fulkerson, שסיבוכיותו לינארית במספר הקשתות כפול גודל הזרימה המירבית. מספר הקשתות כאן הוא , והזרימה המירבית היא

















