מתוך ויקיספר, אוסף הספרים והמדריכים החופשי
נניח שזהו הגרף המקורי:
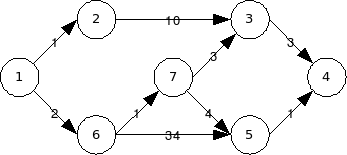 בעיית המסלול הזול ביותר.
בעיית המסלול הזול ביותר.
נבנה גרף חדש כך.
ראשית, נקח את צמתי הגרף  , ונשכפל אותם 3 פעמים, בקבוצות
, ונשכפל אותם 3 פעמים, בקבוצות  ,
,  , ו
, ו . לכל צומת
. לכל צומת  בקבוצה
בקבוצה  , יש צומת
, יש צומת  ב
ב , וצומת
, וצומת  ב
ב . התרשים הבא מראה זאת.
. התרשים הבא מראה זאת.
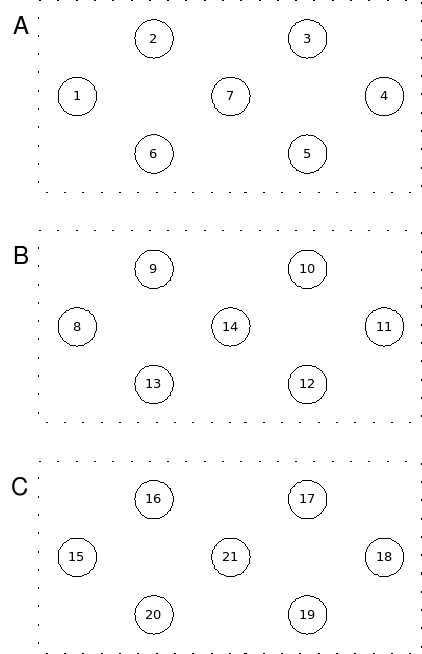 שכפול הצמתים.
שכפול הצמתים.
כעת נוסיף גם קשתות:
- כל קשת בין
 ל
ל (בגרף המקורי) - נמתח אותה בגרף החדש בין
(בגרף המקורי) - נמתח אותה בגרף החדש בין  ב
ב לבין הצומת המתאים ל
לבין הצומת המתאים ל ב
ב .
.
- כל קשת בין
 ל
ל (בגרף המקורי) - נמתח אותה בגרף החדש בין הצומת המתאים ל
(בגרף המקורי) - נמתח אותה בגרף החדש בין הצומת המתאים ל ב
ב לבין הצומת המתאים ל
לבין הצומת המתאים ל ב
ב .
.
התרשים הבא מראה זאת (רק חלק מהקשתות מצויירות).
 הוספת הקשתות.
הוספת הקשתות.
בנוסף נמתח עוד שני סוגי קשתות:
- לכל צומת
 ב
ב , נמתח קשת במחיר
, נמתח קשת במחיר  בין
בין  ב
ב לבין
לבין  ב
ב .
.
- לכל צומת
 ב
ב , נמתח קשת במחיר
, נמתח קשת במחיר  בין
בין  ב
ב לבין
לבין  ב
ב .(לא נצייר קשתות אלו מטעמי נוחות.)
.(לא נצייר קשתות אלו מטעמי נוחות.)
נשים לב שאם כל הגרפים הנ"ל מיוצגים ברשימת שכנויות, אז סיבוכיות הבניה היא  .
.
המשפט הבא מסביר את חשיבות הגרף החדש.
הוכחה: מבניית הגרף החדש, ברור שכל מסלול מ ל
ל ב
ב בגרף החדש, מורכב משני חלקים:
בגרף החדש, מורכב משני חלקים:
- מסלול זהה לחלוטין למסלול מ
 ל
ל בגרף המקורי
בגרף המקורי
- מסלול בעלות 1 ל
 ב
ב , אם החלק הראשון זוגי, ומסלול בעלות
, אם החלק הראשון זוגי, ומסלול בעלות  , אם החלק הראשון אי-זוגי.
, אם החלק הראשון אי-זוגי.
לכן, כל שנותר הוא להריץ את אלגוריתם Dijkstra.
קל לראות שהסיבוכיות הכוללת היא זו של אלגוריתם Dijkstra.















