מבני נתונים ואלגוריתמים - מחברת קורס/אלגוריתמים/תכנון דינאמי/תרגילים/זמן הריצה של הכפלת שרשרת מטריצות תחת Memoization/תשובה

א'

נתבונן בפסוודו-קוד עם memoization:

Min-Time(i, j)
1	if M[i][j] != Nil
2		return M[i][j]

3	if i == j
4		M[i][j] = 0
5		return 0
	
6	min-time = ∞
	
7	for k in [i, ..., j - 1]
8		guess = Min-Time(i, k) + Min-Time(k + 1, j) + PQR(i, k, j)
	
9		if guess M[i][j] < min-time
10			M[i][j] = min-time = guess
				
11	return min-time

נשים לב שאם נניח שכל קריאה רקורסיבית אורכת $\displaystyle O(1)$, אז יש לנו מספר קריאות שכ"א היא $\displaystyle O(1)$ (1-6, 11), ולולאה בת $\displaystyle j-i$ איטרציות, כאשר כל איטרציה היא $\displaystyle O(1)$. זמן הריצה, לכן הוא $\displaystyle T'(i,j)=O(1)+(j-i)\cdot O(1)=\Theta (j-i+1)$.

ב'

ההוכחה חוזרת, למעשה, על זו של דג הסלמון.

נצייר את עץ הקריאות הרקורסיביות, תוך לקיחה בחשבון את נושא הmemoization.

עץ הקריאות הרקורסיביות.

הציור אינו מראה את כל צמתי הקריאה מטעמי נוחות. הצומת $\displaystyle 1,n$ קורא לצומת $\displaystyle 1,1$, בעקיפין לצמתים $\displaystyle 2,2$ ו$\displaystyle 23,36$, ולעוד צמתים. הקווים המקווקווים מציינים שהקריאות אינן בהכרח ישירות.

חלק מהצמתים מודגשים, וחלק אינם:

1. צומת מודגש אם הוא מתאר קריאה "רצינית", כלומר אחת שבה החלק העיקרי בפונקציה מתבצע (שורות 3-11 בMin-Time).
2. צומת אינו מודגש אם הוא מתאר קריאה "פושטית", בה לכל היותר רק חלק הmemoization מתבצע (שורות 1-2 בMin-Time).

נשים לב לנקודות הבאות:

1. אם צומת לא מודגש, אז אין לו ילדים, ובנוסף, הוא $\displaystyle O(1)$ (מדוע?)
2. כל צומת מופיע מודגש פעם אחת (מדוע?)

ננתח כעת בשלבים, לפי הרעיון הבא. בכל שלב:

1. ניקח צומת $\displaystyle i,j$ מודגש שאין לו ילדים מודגשים.
2. ננתח את זמן הריצה שלו, ונרשום את התוצאה בצד. נשים לב שאם לצומת אין ילדים מודגשים, אז כל קריאה רקורסיבית שלו היא אכן $\displaystyle O(1)$ (מפני שזו איננה ממש קריאה רקורסיבית). זמן הריצה שלו, לכן, הוא אכן $\displaystyle T'(i,j)$.
3. נמיר אותו בצומת לא מודגש, מפני שניתחנו כבר את חלק הקוד המסובך בו (ורשמנו אותו בצד). כל שנותר הוא הקריאה לפונקציה, והיא לוקחת $\displaystyle O(1)$.

נתחיל בצומת $\displaystyle 1,1$ המודגש. לצומת זה אין כלל ילדים, ולכן זמן הקריאה הוא בבירור $\displaystyle T'(1)$. נרשום בצד שעד כה הקריאות שעברנו עליהן עלו $\displaystyle T'(1)$, ונחליף את הצומת $\displaystyle 1,1$ בצומת לא מודגש. זה מסמן את העובדה שניתחנו כבר את החלק "עם הבשר" בצומת $\displaystyle 1,1$, וכל שנותר הוא $\displaystyle O(1)$.

עץ הקריאות הרקורסיביות - שלב 1.

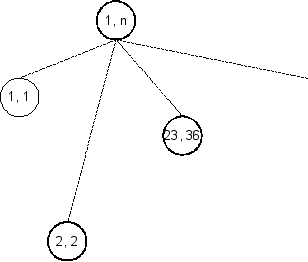
נחזור על אותה הפעולה עבור הצומת $\displaystyle 2,2$.

עץ הקריאות הרקורסיביות - שלב 2.

כנ"ל לגבי הצומת $\displaystyle 23,23$.

עץ הקריאות הרקורסיביות - שלב 3.

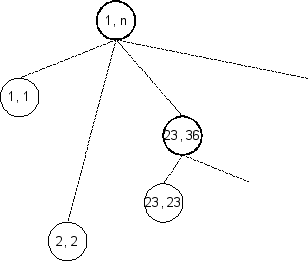
כעת נתבונן בצומת $\displaystyle 23,36$ בשלב בו כל ילדיו אינם מודגשים. כל קריאה רקורסיבית של צומת זה כוללת שני מחירים:

• עצם הקריאה לפונקציה, שעולה $\displaystyle O(1)$
• זמן הקריאה האמיתי, שאותו כבר חייבנו (ורשמנו בצד), ולכן אין צורך לחייב אותו כאן שוב

הפועל היוצא הוא שבשלב זה, מותר לנו לחייב את הצומת אך ורק בקריאות רקורסיביות שעלות כל אחת מהן היא $\displaystyle O(1)$. זה בדיוק $\displaystyle T'(23,36)$.

קל להשתכנע שבשלב בו נחליף את צומת הראש בצומת לא מודגש, רשמנו בצד את כל האיברים מהצורה $\displaystyle T'(i,j)$, כאשר $\displaystyle 1\leq i\leq n$ ו$\displaystyle j\leq i\leq n$. בצורה אחרת, מה שרשום בצד הוא $\displaystyle \sum _{i=1}^{n}\sum _{j=i}^{n}[T'(i,j)]$.

ג'

נשלב את שני הסעיפים הקודמים: $\displaystyle T(1,n)=\sum _{i=1}^{n}\sum _{j=i}^{n}[T'(i,j)]=\sum _{i=1}^{n}\sum _{j=i}^{n}[\Theta (j-i+1)]$.

כבר ראינו כיצד לפשט טור כפול זה בתרגילים בסדרי גדילה.