מבני נתונים ואלגוריתמים - מחברת קורס/אלגוריתמים/סדרי גדילה

דף זה עוסק בסווג פונקציות (מתמטיות) ל"משפחות". כבר ראינו שלפעמים אפשר לקבוע חד-משמעית שאלגוריתם אחד פועל יותר טוב מאחר (עבור קלטים מספיק גדולים), על ידי סווגם למשפחות. אנו נתעניין בהגדרות מדוייקות לסיווגים גמישים יחסית, כמו "משפחת הפונקציות שגדלה כמו פונקציה לינארית", או "משפחת הפונקציות שגדלה יותר מהר מפונקציה לוגריתמית".

כדאי לדעת: בספר הקורס, הפרקים "Growth of Functions" ו"Summations" דנים בנושאים אלה.

הפונקציות בהן נעסוק

לרוב נעסוק בפונקציות המתארות את זמן הריצה של אלגוריתם (או חלק מאלגוריתם). לכן נתמקד בפונקציות מהצורה $\displaystyle f(n)$ בעלות המאפיינים הבאים:

• תחום ההגדרה חיובי שלם: $\displaystyle f(n)$ מוגדרת עבור ערכי $\displaystyle n$ שלמים חיוביים. תחום ההגדרה מציין את גודל הקלט.
• ערך חיובי וסופי: לכל $\displaystyle n$ חיובי ושלם, $\displaystyle 0<f(n)<\infty$. עבור גודל קלט כלשהו, זמן הריצה הוא חיובי ממש וסופי (נזכר שאלגוריתם פועל בזמן סופי עבור קלט בגודל סופי).
• מונוטוניות לא יורדת: $\displaystyle n>m\Rightarrow f(n)\geq f(m)$. נטפל בבעיות שעבורן "יותר קשה" לפתור בעיות גדולות מבעיות קטנות.

קבוצות סדרי הגדילה

הקבוצה $\displaystyle O$

כדאי לדעת: אינטואיטיבית, הקבוצה $\displaystyle O(g(n))$ כוללת את הפונקציות שקצב הגדילה שלהן הוא לכל היותר זה של $\displaystyle g(n)$.

הקבוצה $\displaystyle O(g(n))$ הנה קבוצת כל הפונקציות $\displaystyle f(n)$ כך ש$\displaystyle f(n)$, עבור $\displaystyle n$ גדול מספיק, חסומה מלמעלה ע"י $\displaystyle c\cdot g(n)$ עבור $\displaystyle c>0$ כלשהו.

הגדרה: $\displaystyle O(g(n))=\{f(n)|\exists _{c>0,n_{0}>0}\forall _{n\geq n_{0}}f(n)\leq c\cdot g(n)\}$

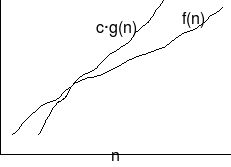
אינטואיציה לאו.

דוגמה: האם (הפונקציה) $\displaystyle n$ שייכת לקבוצה $\displaystyle O(n)$? כן, מפני שעבור $\displaystyle n\geq 1$,‏ $\displaystyle n\leq 1\cdot n$. האם $\displaystyle n+3$ שייכת ל$\displaystyle O(n/2)$? כן, מפני שעבור $\displaystyle n\geq 15$,‏ $\displaystyle n+3\leq 10\cdot (n/2)=5\cdot n$. כדאי לדעת: מדוע בחרנו דווקא בקבועים $\displaystyle c=10$, $\displaystyle n_{0}=15$? אין לכך חשיבות: לפי הגדרת $\displaystyle O$, יש למצוא קבועים כלשהם שעובדים - אין משמעות מיוחדת לקבועים שמצאנו.

דוגמה: האם $\displaystyle n^{2}$שייכת ל$\displaystyle O(n)$? לא. נניח בשלילה שקיימים קבועים $\displaystyle c>0,n_{0}>0$, כך שמתקיים $\displaystyle \forall _{n>n_{0}}n^{2}\leq c\cdot n$. אז $\displaystyle \forall _{n>n_{0}}n\leq c$, שאינו נכון.

למרבה הצער, הסימון $\displaystyle O(g(n))$ משמש לשני דברים שונים: הקבוצה $\displaystyle O(g(n))$, או איבר מהקבוצה $\displaystyle O(g(n))$. שלוש הדוגמאות שראינו מסומנות בד"כ כ$\displaystyle n=O(n)$, ‏$\displaystyle n+3=O(n/2)$, ו$\displaystyle n^{2}\neq O(n)$.

שימו לב: בראותך את הסימון $\displaystyle O(g(n))$, עליך להבין מההקשר האם מדובר אכן בקבוצה או באיבר מתוך הקבוצה.

דוגמה: ראינו שחיפוש לינארי מוצא איבר במקרה הגרוע בזמן $\displaystyle \Theta (1)+\Theta (1)\cdot n$. הזכר שמשמעות $\displaystyle \Theta (1)$הנה קבוע חיובי כלשהו, ולכן ביטוי זה הנו למעשה $\displaystyle k_{1}+k_{2}\cdot n$, עבור $\displaystyle k_{1},k_{2}>0$. האם ביטוי זה $\displaystyle O(n)$? כן, מפני ש$\displaystyle k_{1}+k_{2}\cdot n\leq 2\cdot k_{2}\cdot n$, עבור $\displaystyle n\geq k_{1}/k_{2}$. לרוב רושמים זאת כ$\displaystyle \Theta (1)+\Theta (1)\cdot n=O(n)$.

הקבוצה $\displaystyle \Omega$

כדאי לדעת: אינטואיטיבית, הקבוצה $\displaystyle \Omega (g(n))$ כוללת את הפונקציות שקצב הגדילה שלהן הוא לכל הפחות זה של $\displaystyle g(n)$.

הקבוצה $\displaystyle \Omega (g(n))$ הנה קבוצת כל הפונקציות $\displaystyle f(n)$ כך שכל פונקציה $\displaystyle f(n)$, עבור $\displaystyle n$ גדול מספיק, חסומה מלמטה ע"י $\displaystyle c\cdot g(n)$, עבור $\displaystyle c>0$ כלשהו.

הגדרה: $\displaystyle \Omega (g(n))=\{f(n)|\exists _{n_{0}>0,c>0}\forall _{n\geq n_{0}}f(n)\geq c\cdot g(n)\}$

אינטואיציה לאומגה.

דוגמה: האם $\displaystyle n$שייכת ל$\displaystyle \Omega (n)$? כן, מפני שעבור $\displaystyle n\geq 1$, $\displaystyle n\geq 1\cdot n$. האם $\displaystyle n+3$ שייכת ל$\displaystyle \Omega (n/2)$? כן, משום שעבור $\displaystyle n\geq 1$,‏ $\displaystyle n+3\geq n/2$. האם $\displaystyle n^{2}$שייכת ל$\displaystyle \Omega (n)$? כן, משום שעבור $\displaystyle n\geq 1$,‏ $\displaystyle n^{2}\geq n$.

בדיוק כמו ב$\displaystyle O(g(n))$, גם $\displaystyle \Omega (g(n))$ משמשת לשני דברים: הקבוצה $\displaystyle \Omega (g(n))$, או איבר הקבוצה $\displaystyle \Omega (g(n))$. שלוש הדוגמאות הקודמות נכתבות בד"כ כ$\displaystyle n=\Omega (n)$,‏ $\displaystyle n+3=\Omega (n/2)$, ‏ ו$\displaystyle n^{2}=\Omega (n)$.

שימו לב: בראותך $\displaystyle \Omega (g(n))$, עליך להסיק מההקשר האם מדובר בקבוצה או באיבר מהקבוצה.

דוגמה: האם חיפוש ליניארי רץ במקרה הגרוע בזמן $\displaystyle \Omega (n)$? כן, וודא שהנך מסוגל לשנות את ההוכחה שנתנה לעיל לגבי $\displaystyle O(n)$ כדי להראות זאת.

דוגמה: האם ישנו אלגוריתם (או חלקו) בקורס שאינו $\displaystyle \Omega (1)$? לא משום שנדרש זמן $\displaystyle k>0$עבור קלט בגודל 1, והפונקציות שנטפל בהן הנן מונוטוניות לא יורדות.

הקבוצה $\displaystyle \Theta$

כדאי לדעת: אינטואיטיבית, הקבוצה $\displaystyle \Theta (g(n))$ כוללת את הפונקציות שקצב הגדילה שלהן הוא זה של $\displaystyle g(n)$.

הקבוצה $\displaystyle \Theta (g(n))$ הנה החיתוך של$\displaystyle O(g(n))$ ו$\displaystyle \Omega (g(n))$.

הגדרה: $\displaystyle \Theta (g(n))=O(g(n))\bigcap \Omega (g(n))$

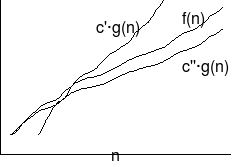
אינטואיציה לתטא.

דוגמה: בהינתן פונקציה $\displaystyle f(n)$כלשהי, האם $\displaystyle f(n)$שייכת ל$\displaystyle \Theta (f(n))$? כן, משום שעבור $\displaystyle n\geq 1$,‏ $\displaystyle f(n)\geq f(n)$, ולכן $\displaystyle f(n)=O(f(n))$; מצד שני, עבור $\displaystyle n\geq 1$,‏ $\displaystyle f(n)\leq f(n)$, ולכן $\displaystyle f(n)=\Omega (f(n))$. כפי שראינו מקודם, כותבים זאת $\displaystyle f(n)=\Theta (f(n))$.

שימו לב: בראותך $\displaystyle \Theta (g(n))$, עליך להסיק מההקשר האם מדובר בקבוצה או באיבר.

דוגמה: האם מציאת איבר במקרה הגרוע בחיפוש ליניארי הנה $\displaystyle \Theta (n)$? כן משום שהיא $\displaystyle O(n)$וגם $\displaystyle \Omega (n)$. האם יש הבדל בין $\displaystyle O(1)$ לבין $\displaystyle \Theta (1)$? לא. אם משהו הוא $\displaystyle \Theta (1)$, אז עפ"י ההגדרה הוא גם $\displaystyle O(1)$. אבל גם אם נאמר לנו רק שהוא $\displaystyle O(1)$ אנחנו יודעים שהוא $\displaystyle \Theta (1)$, משום שכל דבר (שנראה בקורס) הוא $\displaystyle \Omega (1)$.

כדאי לדעת: ניתן לראות שיש שתי דרכים לסימון קבוע חיובי כלשהו: $\displaystyle O(1)$ וכן $\displaystyle \Theta (1)$- משמעותם זהה. לרוב משתמשים ב$\displaystyle O(1)$לצורך כך.

כללי סדרי גדילה

רפלקסיביות

משפט: לכל $\displaystyle f(n)$: $\displaystyle f(n)=O(f(n))$ $\displaystyle f(n)=\Theta (f(n))$ $\displaystyle f(n)=\Omega (f(n))$

(כבר הוכחנו זאת.)

אדיטיביות

משפט: לכל $\displaystyle f(n),g(n)$: $\displaystyle O(f(n))+O(g(n))=O(f(n)+g(n))$ $\displaystyle \Omega (f(n))+\Omega (g(n))=\Omega (f(n)+g(n))$ $\displaystyle \Theta (f(n))+\Theta (g(n))=\Theta (f(n)+g(n))$

כדאי לדעת: הכלל הראשון, לדוגמה, אומר שאם $\displaystyle f_{1}(n)=O(f(n))$וכן $\displaystyle g_{1}(n)=O(g(n))$, אז $\displaystyle f_{1}(n)+g_{1}(n)=O(f(n)+g(n))$.

הוכחה: (1)

עפ"י ההגדרה:

• $\displaystyle f_{1}(n)=O(f(n))$ משמעו שלכל $\displaystyle n\geq n_{0,f}$,‏ $\displaystyle f_{1}(n)\leq c_{f}\cdot f(n)$,‏ עבור $\displaystyle c_{f},n_{0,f}>0$ כלשהם.
• $\displaystyle g_{1}(n)=O(g(n))$ משמעו שלכל $\displaystyle n\geq n_{0,g}$,‏ $\displaystyle g_{1}(n)\leq c_{g}\cdot g(n)$,‏ עבור $\displaystyle c_{g},n_{0,g}>0$ כלשהם.

לכן:

• לכל $\displaystyle n\geq \max\{n_{0,f},n_{0,g}\}$,‏ $\displaystyle f_{1}(n)\leq \max\{c_{f},c_{g}\}\cdot f(n)$.
• לכל $\displaystyle n\geq \max\{n_{0,f},n_{0,g}\}$,‏ $\displaystyle g_{1}(n)\leq \max\{c_{f},c_{g}\}\cdot g(n)$.

מקבלים את התוצאה ע"י חיבור שני האי-שוויונים האחרונים.

סימטריה הפכית

משפט: לכל $\displaystyle f(n),g(n)$,‏ $\displaystyle f(n)=O(g(n))\Leftrightarrow g(n)=\Omega (f(n))$.

הוכחה: $\displaystyle (\Rightarrow )$

$\displaystyle f(n)=O(g(n))\Rightarrow$
$\displaystyle \exists _{c>0,n_{0}>0}\forall _{n\geq n_{0}}f(n)\leq c\cdot g(n)\Rightarrow$
$\displaystyle \exists _{c>0,n_{0}>0}\forall _{n\geq n_{0}}(1/c)\cdot f(n)\leq g(n)\Rightarrow$
$\displaystyle \exists _{c>0,n_{0}>0}\forall _{n\geq n_{0}}g(n)\geq (1/c)\cdot f(n)\Rightarrow$
$\displaystyle g(n)=\Omega (f(n))$

טרנזיטיביות

משפט: לכל $\displaystyle f(n),g(n),h(n)$: $\displaystyle f(n)=O(g(n))\bigwedge g(n)=O(h(n))\Rightarrow f(n)=O(h(n))$ $\displaystyle f(n)=\Omega (g(n))\bigwedge g(n)=\Omega (h(n))\Rightarrow f(n)=\Omega (h(n))$ $\displaystyle f(n)=\Theta (g(n))\bigwedge g(n)=\Theta (h(n))\Rightarrow f(n)=\Theta (h(n))$

הוכחה: דומה למה שראינו באדיטיביות.

שימוש בגבולות

משפט: לכל $\displaystyle f(n),g(n)$,‏ אם $\displaystyle lim_{n\rightarrow \infty }[f(n)/g(n)]$ קיים, ו$\displaystyle lim_{n\rightarrow \infty }[f(n)/g(n)]=c$, אז: $\displaystyle c=0\Rightarrow f(n)=O(g(n))$ $\displaystyle c=\infty \Rightarrow f(n)=\Omega (g(n))$ $\displaystyle 0<c<\infty \Rightarrow f(n)=\Theta (g(n))$

הוכחה: (1)

$\displaystyle \lim _{n\rightarrow \infty }[f(n)/g(n)]=0\Rightarrow$
$\displaystyle \forall _{\epsilon >0}\exists _{n_{0}>0}\forall _{n\geq n_{0}}f(n)/g(n)<\epsilon \Rightarrow$
$\displaystyle \exists _{n_{0}>0}\forall _{n\geq n_{0}}f(n)/g(n)<1\Rightarrow$
$\displaystyle \exists _{n_{0}>0}\forall _{n\geq n_{0}}f(n)<1\cdot g(n)\Rightarrow$
$\displaystyle f(n)=O(g(n))$

שימו לב: ייתכן ש$\displaystyle f(n)=O(g(n))$,‏ $\displaystyle f(n)=\Omega (g(n))$, או $\displaystyle f(n)=\Theta (g(n))$, אך הגבול פשוט אינו קיים.

עכשיו תורכם: מה ההשלכות של כלל הגבול על פולינומים? בצורה אחרת, אם $\displaystyle f(n)=a_{0}+a_{1}\cdot n+\cdots +a_{p}n^{p}$, ו $\displaystyle g(n)=b_{0}+b_{1}\cdot n+\cdots +b_{p}n^{q}$, אז מה קובע את סדר הגדילה בין $\displaystyle f$ ו$\displaystyle g$?

פתרון

לפי כלל הגבול, נוכל לקבוע את הדברים הבאים:

1. אם $\displaystyle p=q$, אז $\displaystyle f(n)=\Theta (g(n))$.
2. אם $\displaystyle p<q$, אז $\displaystyle f(n)=O(g(n))$.
3. אם $\displaystyle p>q$, אז $\displaystyle f(n)=\Omega (g(n))$.

דמיון לאופרטורי השוואה

בדף זה ראינו דרכים לסווג פונקציות לפי סדרי הגדילה שלהן. יש דמיון כלשהו בין הקבוצות שראינו לבין אופרטורי השוואה אלגבריים.

הקבוצה $\displaystyle O$ והייחס $\displaystyle \leq$

הקביעה $\displaystyle f(n)\leq g(n)$ אומרת ש$\displaystyle f(n)$ חסומה מלמעלה על ידי $\displaystyle g(n)$. הקביעה $\displaystyle f(n)=O(g(n))$ אומרת שקצב הגדילה של$\displaystyle f(n)$ חסום מלמעלה על ידי קצב הגידול של $\displaystyle g(n)$. יש דמיון כלשהו בין שתי הקביעות.

ראשית, נשים לב שמתקיים $\displaystyle f(n)\leq g(n)\Rightarrow f(n)=O(g(n))$ (למה?).

יש עוד נקודות דמיון. בין היתר:

• רפלקסיביות: לכל פונקציה $\displaystyle f(n)$ מתקיים $\displaystyle f(n)\leq f(n)$, ובאותו אופן, מתקיים $\displaystyle f(n)=O(f(n))$.
• טרנזיטיביות: לכל $\displaystyle f(n),g(n),h(n)$ מתקיים $\displaystyle f(n)\leq g(n)\bigwedge g(n)\leq h(n)\Rightarrow f(n)\leq h(n)$ ,ובאותו אופן, $\displaystyle f(n)=O(g(n))\bigwedge g(n)=O(h(n))\Rightarrow f(n)=O(h(n))$

הקבוצה $\displaystyle \Omega$ והייחס $\displaystyle \geq$

הקביעה $\displaystyle f(n)\geq g(n)$ אומרת ש$\displaystyle f(n)$ חסומה מלמטה על ידי $\displaystyle g(n)$. הקביעה $\displaystyle f(n)=\Omega (g(n))$ אומרת שקצב הגדילה של$\displaystyle f(n)$ חסום מלמטה על ידי קצב הגידול של $\displaystyle g(n)$. יש דמיון כלשהו בין שתי הקביעות.

ראשית, נשים לב שמתקיים $\displaystyle f(n)\geq g(n)\Rightarrow f(n)=\Omega (g(n))$ (למה?).

יש עוד נקודות דמיון. בין היתר:

• רפלקסיביות: לכל פונקציה $\displaystyle f(n)$ מתקיים $\displaystyle f(n)\geq f(n)$, ובאותו אופן, מתקיים $\displaystyle f(n)=\Omega (f(n))$.
• טרנזיטיביות: לכל $\displaystyle f(n),g(n),h(n)$ מתקיים $\displaystyle f(n)\geq g(n)\bigwedge g(n)\geq h(n)\Rightarrow f(n)\geq h(n)$ ,ובאותו אופן, $\displaystyle f(n)=\Omega (g(n))\bigwedge g(n)=\Omega (h(n))\Rightarrow f(n)=\Omega (h(n))$

הקבוצה $\displaystyle \Theta$ והייחס $\displaystyle =$

הקביעה $\displaystyle f(n)=g(n)$ אומרת ש$\displaystyle f(n)$ שווה ל$\displaystyle g(n)$. הקביעה $\displaystyle f(n)=\Theta (g(n))$ אומרת שקצב הגדילה של$\displaystyle f(n)$ שווה לקצב הגידול של $\displaystyle g(n)$. יש דמיון כלשהו בין שתי הקביעות.

ראשית, נשים לב שמתקיים $\displaystyle f(n)=g(n)\Rightarrow f(n)=\Theta (g(n))$ (למה?).

יש עוד נקודות דמיון. בין היתר:

• רפלקסיביות: לכל פונקציה $\displaystyle f(n)$ מתקיים $\displaystyle f(n)=f(n)$, ובאותו אופן, מתקיים $\displaystyle f(n)=\Theta (f(n))$.
• טרנזיטיביות: לכל $\displaystyle f(n),g(n),h(n)$ מתקיים $\displaystyle f(n)=g(n)\bigwedge g(n)=h(n)\Rightarrow f(n)=h(n)$ ,ובאותו אופן, $\displaystyle f(n)=\Theta (g(n))\bigwedge g(n)=\Theta (h(n))\Rightarrow f(n)=\Theta (h(n))$.

עוד נקודות דמיון

יש עוד נקודות דמיון, לדוגמה:

1. סימטריה הופכית: לכל שתי פונקציות $\displaystyle f(n),g(n)$,‏ $\displaystyle f(n)\leq g(n)\Leftrightarrow g(n)\geq f(n)$, ובאותו אופן, $\displaystyle f(n)=O(g(n))\Leftrightarrow g(n)=\Omega (f(n))$.
2. לכל שתי פונקציות $\displaystyle f(n),g(n)$,‏ $\displaystyle f(n)=g(n)\Leftrightarrow f(n)\leq g(n)\bigwedge f(n)\geq g(n)$, ובאותו אופן, $\displaystyle f(n)=\Theta (g(n))\Leftrightarrow f(n)=O(g(n))\bigwedge f(n)=\Omega (g(n))$.

מגבלות הדמיון

לדמיון בין הקבוצות לאופרטורים שראינו יש גם מגבלות. בין היתר:

1. לא תמיד נכון ש$\displaystyle 2\cdot f(n)\leq f(n)$, אך תמיד נכון ש$\displaystyle 2\cdot f(n)=O(f(n))$.
2. תמיד מתקיים ש$\displaystyle f(n)\leq g(n)\Rightarrow 2^{f(n)}\leq 2^{g(n)}$, אך לא תמיד מתקיים $\displaystyle f(n)=O(g(n))\Rightarrow 2^{f(n)}=O(2^{g(n)})$.

עכשיו תורכם: נמק נקודות אלו.

דוגמה לשילוב מספר כללים

נפשט את הביטוי $\displaystyle f(n)=\sum _{i=1}^{n}[\Theta (1)+\Theta (i)]$.

ראשית, נשים לב ש $\displaystyle \Theta (1)+\Theta (i)=\Theta (i+1)$ מכלל האדיטיביות. אבל $\displaystyle \Theta (i+1)=\Theta (i)$, מפני ששני הביטויים בתוך ה$\displaystyle \Theta$ הם פולינומים בהפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "http://localhost:6011/he.wikibooks.org/v1/":): {\displaystyle \displaystyle i} בעלי דרגה 1. לכן נקבל $\displaystyle f(n)=\sum _{i=1}^{n}[\Theta (i)]$.

כעת נשתמש שוב באדיטיבות:

$\displaystyle f(n)=$
$\displaystyle \sum _{i=1}^{n}[\Theta (i)]=$
$\displaystyle \Theta (1)+\Theta (2)+\cdots +\Theta (n)=$
$\displaystyle \Theta (1+2+\cdots +n=$
$\displaystyle \Theta \left(\sum _{i=1}^{n}[i]\right)$

אבל $\displaystyle \sum _{i=1}^{n}[i]={\frac {n(n+1)}{2}}$, מפני שזה טור חשבוני פשוט. לכן נקבל $\displaystyle f(n)=\Theta \left({\frac {n(n+1)}{2}}\right)$. כלומר, $\displaystyle \Theta$ של פולינום ב$\displaystyle n$ בעל דרגה 2. לסיכום, לכן, נקבל $\displaystyle f(n)=\Theta (n^{2})$.

סיכום

בחיפוש לינארי ובינרי ראינו דוגמות ראשונות של ניתוח אלגוריתמים. דף זה עסק בסדרי גדילה של פונקציות.

בהנתן אלגוריתם כלשהו, נוכל לשאול לגביו מספר שאלות, לדוגמה:

1. מהו זמן הריצה של האלגוריתם במקרה הטוב ביותר?
2. מהו זמן הריצה של האלגוריתם במקרה הגרוע ביותר?
3. מהו זמן הריצה של האלגוריתם במקרה הממוצע? (לא נעסוק בכך בקורס זה, עם זאת).

לעתים נוכל לשאול שאלות מפורטות יותר אפילו:

1. מהו זמן הריצה הטוב ביותר של חיפוש בינרי בהנחה שהאיבר נמצא במערך?
2. מהו זמן הריצה הגרוע ביותר של חיפוש לינארי בהנחה שהאיבר אינו נמצא במערך?

בכל פעם שאנו מקבלים אלגוריתם ושאלה מסוג זה, התשובה הינה פונקציה (מתמטית) של $\displaystyle n$, גודל הקלט. נוכל להשתמש בקבוצות סדרי הגדילה שראינו כאן כדי לסווג את הפונקציה (המתמטית). כך לדוגמה, נוכל להגיד על אלגוריתם כלשהו "הוא פועל במקרה הגרוע ביותר בערך כמו פונקציה לינארית", או "הוא פועל במקרה הטוב ביותר פחות מאיזושהי פונקציה שורשית".

כדאי לדעת: במציאות, השאלות המעניינות ביותר לגבי אלגוריתמים הן לרוב זמן הריצה הגרוע והממוצע שלהם (זמן הריצה הטוב ביותר שלהם כמעט אף פעם לא מעניין). בקורס זה (שאינו מניח ידע בהסתברות), ננתח כמעט תמיד את זמן הריצה הגרוע של אלגוריתמים.

הפרק הקודם: חיפוש לינארי ובינרי

סדרי גדילה תרגילים

הפרק הבא: נוסחאות נסיגה