מערכות ספרתיות ומיקרו מחשבים/בסיסים ומעברי בסיס: הבדלים בין גרסאות בדף
מ שוחזר מעריכה של 213.151.48.142 (שיחה) לעריכה האחרונה של Mr.Shoval |
|||
| שורה 74: | שורה 74: | ||
<math>\!\, 1452=1\cdot1000+4\cdot100+5\cdot10+2=1\cdot10^3+4\cdot10^2+5\cdot10^1+2\cdot10^0 </math> |
<math>\!\, 1452=1\cdot1000+4\cdot100+5\cdot10+2=1\cdot10^3+4\cdot10^2+5\cdot10^1+2\cdot10^0 </math> |
||
</p> |
</p> |
||
אנו רואים כי הבסיס המשותף לכל |
אנו רואים כי הבסיס המשותף לכל האיברים הוא 10. |
||
בסיס הספירה הבינארית הוא 2 (לספירה זו שני סימנים), |
|||
לכן נפרק את המספר הבינארי הבא בהתאם לפירוק המספר העשרוני:<br /> |
|||
<p align="left"> |
|||
<math>\!\, 1101 = 1\cdot2^3+1\cdot2^2+0\cdot2^1+1\cdot2^0= |
|||
8+4+0+1=13 |
|||
</math> |
|||
</p> |
|||
מכאן שהמספר 1101 בספירה בינארית שקול למספר 13 בספירה עשרונית.<br /> |
|||
לכן נציג '''נוסחה''' כללית, למעבר מספרה המוצגת בבסיס בינארי לבסיס עשרוני |
|||
(באגף השמאלי מופיע המספר בספרות בינאריות, ומימין משמעותו בספרות עשרוניות): |
|||
<p align="left"> |
|||
<math>\!\, a_1a_2a_3...a_n = a_1\cdot2^{n-1} + a_2\cdot2^{n-2} + a_3\cdot2^{n-3} +... + a_n\cdot2^0 |
|||
</math><br /> |
|||
<div style="direction: rtl;"><br /> |
|||
או בנוסחת הנסיגה כשX מייצג את מס' הספרות של המס' הבינארי וY מייצג את הערך העשרוני של המס' הבינארי ללא הספרה השמאלית ביותר וידוע ש a(0) = 0 ו- a(1) = 1</div> |
|||
<br /> |
|||
<div style="direction: ltr;"><math>a(n) = 2^{X-1} + Y</math><br /></div> |
|||
לדוגמה |
|||
<br /> |
|||
<div style="direction: ltr;"><math>a(1101) = 2^3 + a(101) = 8 + 5 = 13</math></div> |
|||
<br /> |
|||
<div style="direction: ltr;"><math>a(101)= 2^2 + a(01) = 4 + 1 = 5</math></div> |
|||
<br /> |
|||
<div style="direction: ltr;"><math>a(01) = 1</math></div> |
|||
</p> |
|||
==== מעבר ממספרים עשרוניים למספרים בינאריים ==== |
==== מעבר ממספרים עשרוניים למספרים בינאריים ==== |
||
גרסה מ־15:18, 18 באפריל 2013
| הדף נמצא בשלבי עבודה: כדי למנוע התנגשויות עריכה ועבודה כפולה אתם מתבקשים שלא לערוך ערך זה בטרם תוסר הודעה זו, אלא אם כן תיאמתם זאת עם מניחי התבנית. | |||
| אם הדף לא נערך במשך שבוע ניתן להסיר את התבנית ולערוך אותו, אך רצוי לתת קודם תזכורת בדף שיחת הכותבים. | |||
לפני שננסה להבין איך מתבצעים החישובים בבסיסי ספירה שונים בכלל ובבסיס בינארי במחשב בפרט,ננסה קודם להבין למה אנחנו מתכוונים כאשר אנחנו מדברים על המספרים המוכרים לנו. למשל נניח כי מציעים לנו לבחור בין 3 סכומים : 3000 ש"ח 5000 ש"ח או 50000 ש"ח אנו מרגישים אינטואיטיבית את השוני בין המספרים בכך שיש חשיבות למספרים עצמם (3 או 5) וגם למקומם (5000 או 50000).שיטת ספירה זו שאנו משתמשים בה נקראת שיטת ספירה פוזיציונאלית - מבוססת על מקום.כדי להבין טוב יותר את משמעות השיטה נסתכל למשל על המספר 243. אפשר לרשום מספר זה בצורה הבאה:
כדאי לדעת: *חזקה טבעית של מספר מציינת את מספר הפעמים שהמספר נכפל בעצמו למשל:
|
אנו רואים שהספרה 10 וחזקותיה (במקרה זה 1 ו 100) חוזרות לכל ארוך הפירוק שביצענו והן מופיעות בצמוד לספרות שהופיעו במספר המקורי. בצורה אחרת אפשר לומר כי כל אחת משלושת הספרות במספר 243 קיבלה משקל שונה. כל אחת מהן הוכפלה בגורם שערכו 10 בחזקת מיקום הספרה (כאשר מיקום הספרה הימנית ביותר הוא 0) דבר זה אינו מקרי והוא נובע מכך כי אנו סופרים בבסיס עשרוני.ננסח כלל חשוב שיעזור לנו בעתיד לבצע פירוקים דומים:
בזמן פירוק מספר לפי הבסיס בו הוא כתוב כל ספרה משוקללת (מוכפלת ב - ) ע"י בסיס הספירה בחזקת מיקום הספרה
נפתור מספר תרגילים להמחשת כלל זה:
תרגיל 2.1
פרקו לפי בסיס 10 את המספר 8754
פתרון
ראשית נמספר את מיקום הספרות מימין לשמאל,כאשר נקבע כי המיקום של הספרה הימנית ביותר במספר(4) הוא 0
.... צריך להשלים
נחזור לבעיה שהתחלנו ממנה והיא: איך אפשר לספור בבסיס 2 למשל, כלומר אם נתון לנו מספר בינארי איך נדע לאיזה מספר עשרוני ישן ומוכר הוא שווה. מתברר שאם אנו מבינים היטב איך בנוי בסיס 10 לעבור לבסיס 2 לא מהווה שום בעיה. אם בבסיס העשרוני היו במלאי שלנו 10 ספרות והן: 0 1 2 3 4 5 6 7 8 9 שדרשו מאיתנו להשתמש בחזקות של 10, בבסיס הבינארי עומדת לררשותינו 2 ספרות בלבד 0 ו 1 ולכן החזקות שנשתמש בהן יהיו בהתאם חזקות של 2.
תרגיל 2.2 :
פרקו לפי בסיס 2 את המספר הבינארי 101
פתרון:
ראשית כמו בתרגיל 2.1 נמספר את מיקום הספרות מימין לשמאל,כאשר נקבע כי המיקום של הספרה הימנית ביותר במספר(1) הוא 0
כעת נכפול כל ספרה ב 2 בחזקת המיקום שלו:
קיבלנו כי המספר הבינארי 101 הוא 5 בבסיס עשרוני שונה מאוד(!) מ 101 העשרוני "הרגיל". כדי למנוע בלבול לעתים מקובל לרשום את המספר יחד עם הבסיס שלו כך : נקפיד לציין זאת בהמשך בכל מקום שבו חוסר בהירות כזה יכול להתעורר.
2.2 בסיסי ספירה חשובים
קיים מספר אינסופי של בסיסי ספירה אפשרים. למעשה כל מה שצריך כדי לנסח בסיס ספירה הוא:
- למצוא כמה ספרות אנחנו רוצים שהבסיס יכלול
- לכל ספרה לתת סימן יחודי כמו למשל 1.
נציג להלן כמה מהבסיסים הנפוצים והשימושים ביותר:
בסיס ספירה עשרוני(10)
זהו כמובן הבסיס שכולנו רגילים אליו ומרגישים אינטואטיבית
את משמעות ספרותיו למשל: 10234
בסיס ספירה בינארי(2)
בסיס בינארי היא שיטת ספירה לפי בסיס 2, שפותחה על ידי המתמטיקאי גוטפריד וילהלם לייבניץ במאה ה-17. בייצוג זה קיימות רק שתי ספרות: "0" ו-"1", ובאמצעותן ניתן לבטא כל מספר טבעי.
בשיטה זו, ערכה של כל ספרה "1" הוא כאשר n הוא מיקום הספרה מימין, החל מ-0.
לדוגמה, הייצוג של המספרים הטבעיים הקטנים מ-8 יהיה:
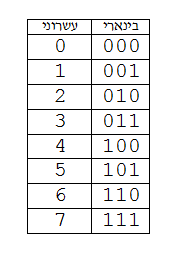
בסיס בינארי משמש כיום בעיקר בתחום מדעי המחשב, זאת כיוון שבמעגלים לוגיים אלקטרוניים נוח להסתפק בהבחנה בין שתי רמות מתח בלבד, גבוה ונמוך, המיוצגות על ידי "1" ו-"0" בהתאמה. ולכן זהו הבסיס הטבעי להביע בו מספרים במחשב המורכב ממעגלים כאלו.
מאפיינים נוספים ייחודיים לשיטה זו הם הדמיון שלה לבסיס הסטנדרטי באלגברה לינארית, וכן היותה הבסיס הנמוך ביותר בשימוש נפוץ בייצוג מספרים.
קיימות שיטות ייצוג אחרות, המבוססות על הבסיס הבינארי, כמו קוד גריי, שיטת המשלים ל-2 המאפשרת ייצוג מספרים שליליים, או ייצוג נקודה צפה של מספרים רציונליים.
מעבר ממספרים בינאריים למספרים עשרוניים
בסיס הספירה העשרונית הוא 10, משום שלספירה זו 10 סימנים.
פירוק מספר עשרוני:
אנו רואים כי הבסיס המשותף לכל האיברים הוא 10.
בסיס הספירה הבינארית הוא 2 (לספירה זו שני סימנים),
לכן נפרק את המספר הבינארי הבא בהתאם לפירוק המספר העשרוני:
מכאן שהמספר 1101 בספירה בינארית שקול למספר 13 בספירה עשרונית.
לכן נציג נוסחה כללית, למעבר מספרה המוצגת בבסיס בינארי לבסיס עשרוני
(באגף השמאלי מופיע המספר בספרות בינאריות, ומימין משמעותו בספרות עשרוניות):
או בנוסחת הנסיגה כשX מייצג את מס' הספרות של המס' הבינארי וY מייצג את הערך העשרוני של המס' הבינארי ללא הספרה השמאלית ביותר וידוע ש a(0) = 0 ו- a(1) = 1
לדוגמה
מעבר ממספרים עשרוניים למספרים בינאריים
מעבר ממספר עשרוני למספר בינארי יתבצע באמצעות המרה של המספר העשרוני למספרים בחזקת 2 (בסיס 2) וסידורם בסדר יורד.
דוגמה: ניקח את המספר 73. תחילה נמצא את החזקה בבסיס 2 הקרובה ביותר למספר (אך קטנה ממנו). החזקה הקטנה ביותר המתאימה היא:
כדי להגיע למספר 73 נצטרך להוסיף עוד חזקות בעלות בסיס 2. נבדוק אם
יתאים לנו:
קיבלנו מספר גדול מהמספר 73. לכן יש לחפש חזקה קטנה יותר.נבדוק אם יתאים לנו:
קיבלנו מספר גדול מהמספר 73. לכן יש לחפש חזקה קטנה יותר.נבדוק אם
יתאים לנו:
המספר 72 קטן מהמספר 73, לכן החזקה
מתאימה לנו.
כדי להגיע מ-72 ל-73 נצטרך להוסיף עוד מספר. ברור כי
ו-
לא יתאימו לנו, אבל
יתאים לנו.
ולכן פירוק המספר 73 לחזקות בעלות בסיס 2 הוא:
כדי להגיע למספר הבינארי המתאים, נוסיף את החזקות החסרות בין החזקות הללו:
כלומר, חזקות שהשתמשנו בהן, הוכפלו ב-1 וחזקות שלא השתמשנו בהם, הוכפלו ב-0. המספר הבינארי שלנו מורכב מהמקדמים של מספרי החזקות. מכאן ש-73 בספירה בינארית הוא:
שיטה נוספת למעבר ממספרים עשרוניים למספרים בינאריים
שיטה נוספת, וקלה יותר,להמרת מספרים מבסיס עשרוני לבסיס בינארי מתבצעת על ידי חלוקה חוזרת של המספר העשרוני ב-2 ובדיקת השארית.
נדגים את השיטה:
כדי להמיר את המספר העשרוני 73 לבסיס בינארי נחלק אותו ב-2.
התוצאה תהיה 36 ושארית של 1 (שהרי 36x2 + 1 = 73).
משמעות השארית 1 היא שבבסיס בינארי הספרה הימנית ביותר היא 1.
נמשיך ונחלק את התוצאה 36 ב-2.
קיבלנו 18 ושארית 0. לכן, עד כה ההמרה הבינארית שלנו היא 01.
נמשיך ונחלק את התוצאה 18 ב-2.
קיבלנו 9 ושארית 0. לכן, עד כה ההמרה הבינארית שלנו היא 001.
נמשיך ונחלק את התוצאה 9 ב-2.
קיבלנו 4 ושארית 1. לכן, עד כה ההמרה הבינארית שלנו היא 1001.
נמשיך ונחלק את התוצאה 4 ב-2.
קיבלנו 2 ושארית 0. לכן, עד כה ההמרה הבינארית שלנו היא 01001.
נמשיך ונחלק את התוצאה 2 ב-2.
קיבלנו 1 ושארית 0. לכן, עד כה ההמרה הבינארית שלנו היא 001001.
נמשיך ונחלק את התוצאה 1 ב-2.
קיבלנו 0 ושארית 1. לכן, עד כה ההמרה הבינארית שלנו היא 1001001.
למעשה, כעת ניתן להמשיך ולחלק את 0 ב-2 אינספור פעמים אך התוצאה תמיד תשאר אפס ושארית אפס.
ולכן זהו המספר הסופי בבסיס בינארי: 1001001
(אם נמשיך את החלוקה ב-2 נקבל מספר מהצורה 000001001001..., השווה למספר המצומצם 1001001.)
קישורים חיצוניים
- המחשה אינטראקטיבית של ספירה בבסיס בינארי והקסדצימלי מתוך אתר לילדים המלמד מושגים במדעי המחשב
בסיס ספירה אוקטלי(8)
בבסיס ספירה זה משתמשים ב 8 ספרות (0,1,2,3,4,5,6,7) מספר אוקטלי לדוגמא הינו 73143234 (שימו לב שאין ספרות הגדולות מ 7 במספר)
בסיס ספירה הקסדצימלי(16)
בבסיס זה עושים שימוש ב 16 ספרות ומיד אנו מגלים קושי מסויים הרי אנו מכירים רק 10 ספרות: 0,1,2,3,4,5,6,7,8,9
איך נסמן את 6 הסימנים הנוספים?
למעשה צריך כאן להזכר שאין דבר מיוחד בבסיס העשרוני הספרות שאנו רגילים אליהן הן סימנים שלא היו קיימים תמיד אלה הומצאו בזמן כלשהו בעבר (למעשה הספרות "הרגילות" שלנו הן וריאציה אירופאית על הספרות ההודו-ערביות) לכן אם צריך עוד סימנים מיוחדים שיציינו כמות מסוימת פשוט "נמציא" צורות חדשות. במקרה הזה מקובל לתת לספרות מ- 10 עד 15 את צורת האותיות הראשיות הראשונות בא"ב האנגלי.
A=10 B=11 C=12 D=13 E=14 F=15
מספר הקסדצימלי לדוגמא: 123AB32
2.3 מעבר לבסיס עשרוני מבסיס כלשהו
ראינו בכמה דוגמאות כיצד ניתן לעבור מבסיס כלשהו לבסיס עשרוני אבל מה עושים במקרה ההפוך? דהינו נניח כי נתון לי מספר עשרוני איך אפשר לדעת כיצד ניתן להציגו בבסיס אחר למשל בינארי? קיימת שיטה קבועה לעשות זאת, אלגוריתם שמאפשר לעשות את המעבר עבור כל בסיס. נציג אותו
בתרגיל.
כדאי לדעת: חילוק מספרים :שלם ושאריתחילוק של שני מספרים תמיד מורכב משני חלקים : מספר הפעמים שהמספר המחלק נכנס למחולק במלאו והשארית שמשמעותה כמה צריך להוסיף כדי להגיע למספר המחלוק. |
תרגיל 2.3 :
הצג את המספר: בבסיס 5
פתרון:
כדאי לדעת: השיטה שתעזור לנו כדי לפתור את התרגיל היא השיטה הבאה:1. נצייר טבלה עם שלוש כותרות "חישוב" "שלם" ו"שארית" ומספר שורות כמספר הספרות 2. נחלק את המספר לפי הבסיס שלו ונרשום את החלק השלם ואת השארית בעמודות המתאימות 3. נחזור לשלב 1 ונשתמש בחלק השלם של התוצאה בתור המספר לחילוק בשלב הבא אם התקבל 0 בחלק השלם סיימנו! נקרא את הספרות מהאחרונה שהתקבלה לראשונה |
| הפרק הקודם: הקדמה |
בסיסים ומעברי בסיס | הפרק הבא: מבוא לפעולות במעבד המחשב |
























