מבני נתונים ואלגוריתמים - מחברת קורס/גרפים/אלגוריתמים למציאת עפ"מ/תרגילים/תנאי לעפ"מ יחידי/תשובה

תשובה שגויה ע"י שימוש באלגוריתם Kruskal

כדאי לדעת: אלגוריתם Kruskal פועל כך. ראשית הוא ממיין את קשתות הגרף על פי העלות (או המשקל, תלוי בהגדרה), ולאחר מכן הוא בוחר קשתות מעצים שונים על פי סדר המיון.

להלן הוכחה שגויה לקיום עפ"מ יחידי:

הוכחה: נשים לב שאם הקשתות בעלות משקלים שונים, תוצאת המיון נקבעת חד משמעית, ולכן יש רק עפ"מ יחיד שאלגוריתם Kruskal יחזיר. לכן יש עפ"מ יחיד.

תשובה זו אינה נכונה, מפני שהיא מתייחסת לאלגוריתם Kruskal בלבד. אפשר עדיין לטעון, לדוגמה, שאלגוריתם Prim יחזיר עפ"מ שונה במקרה זה (בהמשך נראה שזה בלתי אפשרי, אלא שאי אפשר להסיק זאת מהטענה שהוצגה עד עתה).

תשובה שגויה ע"י שימוש לא נכון באינדוקציה

להלן הוכחה שגויה באינדוקציה:

הוכחה: האינדוקציה היא על מספר הצמתים, $\displaystyle \vert V\vert$.

(בסיס האינדוקציה) כאשר $\displaystyle \vert V\vert =1$ אז יש צומת יחיד והעפ"מ בוודאי יחידי.

(מעבר האינדוקציה), ניקח צומת כלשהו $\displaystyle u$, ונמצא את העפ"מ $\displaystyle T_{1}$ של הצמתים $\displaystyle V\setminus u$. קבוצה זו קטנה ב1 מ$\displaystyle \vert V\vert$, ולכן יש לה עפ"מ יחידי. נותר לחבר את $\displaystyle u$ ל$\displaystyle T_{1}$, וברור שנעשה זאת דרך הקשת הזולה ביותר בין $\displaystyle u$ לבין צומת ב$\displaystyle T_{1}$.

מעבר אינדוקציה שגוי לעפ"מ יחדי.

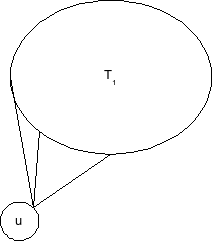
מדוע ההוכחה שגויה? היא מוכיחה שיש עפ"מ יחיד מבין העפ"מים בהם יוצאת קשת יחידה מ$\displaystyle u$. היא כלל אינה סותרת את קיומו של עפ"מ כמו בתרשים הבא, שלכאורה יכול להיות אופטימאלי גם כן:

סתירה מעבר אינדוקציה שגוי לעפ"מ יחדי.

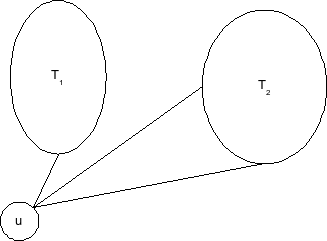
כדאי לדעת: חדי העין יזהו שאין הבדל ממשי בין הטעות כאן לבין הטעות הקודמת. האינדוקציה כאן היא למעשה הפעלת אלגוריתם Prim תחת הנחות שגויות שמקבלת תוצאה כללית לגבי כל העפ"מים האפשריים.

תשובה ע"י שיקול הקשת הזולה ביותר בגרף

ראשית נוכיח את המשפט הבא.

משפט: נניח ש$\displaystyle G=(V,E)$ הוא גרף, $\displaystyle u,v\in V$ הם שני צמתים, ו$\displaystyle e=(u,v)\in E$ היא קשת. "כווץ" גרף בין שני צמתים - לפני נגדיר כעת את הגרף $\displaystyle G'=(V',E')$ כגרף המתקבל מ"כיווץ" $\displaystyle u$ ו$\displaystyle v$ לצומת יחיד, $\displaystyle uv$. "כווץ" גרף בין שני צמתים - אחרי נגדיר כ$\displaystyle T'$ את קשתות העפ"מ ב$\displaystyle G'$. אז קשתות עפ"מ זה יחד עם $\displaystyle (u,v)$,‏ כלומר $\displaystyle 'T\bigcup {(u,v)}$ ,‏ הם בהכרח קשתות העץ הזול ביותר הפורס את $\displaystyle G$ מבין העצים הפורשים שמשתמשים ב$\displaystyle e=(u,v)$.

הוכחה: ראשית ברור שהתוצאה היא עץ. נניח ש$\displaystyle x$ ו$\displaystyle y$ הם שני צמתים. קל לראות שאם יש מסלול מ$\displaystyle x$ ל$\displaystyle y$ ב$\displaystyle G'$ המשתמש בקשתות $\displaystyle T'$ בלבד , אז יש מסלול מ$\displaystyle x$ ל$\displaystyle y$ ב$\displaystyle G'$ המשתמש בקשתות $\displaystyle T'\bigcup {(u,v)}$ בלבד. קל לראות שאם $\displaystyle T'\bigcup {(u,v)}$ מכיל מעגל, אז גם $\displaystyle T'$ מכיל מעגל.

כעת ברור גם שמדובר בעץ הזול ביותר. נניח שיש עץ פורש זול יותר $\displaystyle T''\bigcup {(u,v)}$. אז גם $\displaystyle T''$ עץ פורש זול יותר ב$\displaystyle G'$, דבר שסותר את הנחתנו ש$\displaystyle T'$ היא קבוצת קשתות עפ"מ.

בעזרת המשפט הקודם נוכל להוכיח שיש עפ"מ יחידי באינדוקציה (הפעם בצורה נכונה).

הוכחה: האינדוקציה היא על מספר הצמתים, $\displaystyle |V|$.

(בסיס האינדוקציה) כאשר $\displaystyle |V|=1$ אז יש צומת יחיד והעפ"מ בוודאי יחידי.

(מעבר האינדוקציה) ניקח את הקשת הקלה ביותר בגרף $\displaystyle e=(u,v)$. כבר הוכחנו שקשת זו היא חלק מכל עפ"מ. כעת "נכווץ" את הגרף ע"י הפיכת שני הצמתים, $\displaystyle u$ ו$\displaystyle v$, לצומת יחיד. מהנחת האינדוקציה נובע שקיים כעת עפ"מ יחיד (שהרי מספר הצמתים ירד ב1). המשפט הקודם אומר שקשתות כל עפ"מ שהתקבל בגרף המכווץ, יחד עם $\displaystyle e$, הן בדיוק קשתות העפ"מ בגרף המקורי. נובע לכן שיש עפ"מ יחיד.

תשובה ע"י שיקול הקשת היקרה ביותר במעגל

נניח בשלילה שיש שני עפ"מים שונים: $\displaystyle T_{1}$ ו$\displaystyle T_{2}$. היות שהעפ"מים שונים אך מספר קשתותיהם שווה, קיימת בהכרח קשת $\displaystyle e$ השייכת ל$\displaystyle T_{2}$ אך לא ל$\displaystyle T_{1}$. הוספת קשת זו ל$\displaystyle T_{1}$ בהכרח תיצור מעגל. נגדיר כ$\displaystyle e'$ את הקשת הכבדה ביותר על פני המעגל, וניזכר שקשת זו איננה חלק מאף עפ"מ. כעת אם $\displaystyle e'=e$, אז $\displaystyle T_{2}$ אינה עפ"מ; מצד שני, אם $\displaystyle e'\neq e$, אז $\displaystyle T_{1}$ אינה עפ"מ. בכל מקרה, לא ייתכן מעגל כזה, ולכן בהכרח אין שני עפ"מים שונים.